Принципиальная схема.
F(t)
Передаточные функции звеньев системы. Датчик Температуры: Tд Tд U(t)p + U(t) = KдΩ(t) U(t)(Tдp + 1) = KдΩ(t) W1 =
Усилитель Постоянного Тока: I = U I(t) = U(t) W2 =
Электромеханический Преобразователь: m mh(t)p2 + W3 =
Объект Регулирования: To To Ω(t)p + Ω(t) = Koh(t) + f(t) Ω(t)(Top + 1) = Koh(t) + f(t) W4 =
Преобразование схемы в одноконтурную с подстановкой данных.
Ω1 Ω2
Передаточные функции разомкнутой и замкнутой систем. W(p)раз =
W(p)замк =
W(p)замк = Построение АФЧХ, АЧХ, ФЧХ
Зададим передаточную функцию САУ:
Wр(ω)=
Определим передаточную функцию замкнутой системы:
WЗ(ω) =
ФЧХ замкнутой системы:
АЧХ замкнутой системы:
АФЧХ замкнутой системы:
АЧХ разомкнутой системы:
ФЧХ разомкнутой системы:
АФЧХ разомкнутой системы:
Определение устойчивости разомкнутой САУ
Критерий Рауса: Характеристическое уравнение берем из знаменателя передаточной функции разомкнутой системы.
Характеристическое уравнение:
В первом столбике таблицы Рауса коэффициенты не меняют своего знака, значит, система устойчива и не имеет правых корней.
Построение ЛАЧХ, ЛФЧХ. W(p)раз =
20Lg(k) = 20Lg(0.119) = -18.5
ω1 = ω2 = ω3 = φ(ω) = 0 – arctg(0.45ω) + arctg(0.4ω) – arctg
Исходя из графика АФЧХ замкнутой системы, делаем вывод о том, что исходная система устойчива.
Построение желаемой ЛАЧХ: Выбираем тип ЛАЧХ – 3.
Тогда: σ = 25% tp = 1.1
ωc = 7 ωc * tp = 5.5 tp = 0.78
Тогда: ω1ж = ω1 = 0,7 ω2ж = 2,4 ω3ж = 31
|

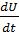 + U = KдΩ
+ U = KдΩ =
= 
 = 1
= 1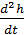 +
+ 
 + Ch = KhI
+ Ch = KhI =
= 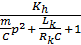
 + Ω = Koh + f(t)
+ Ω = Koh + f(t) =
= 









 =
=  =
= 
 =
= 






 = 0
= 0
 = 0.7
= 0.7 = 2.2
= 2.2 = 2.5
= 2.5




