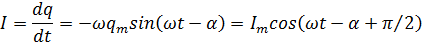Дифференциальное уравнение свободных затухающих колебаний
линейной системы
линейной системы имеет вид
где s − колеблющаяся величина, δ = const — коэффициент затухания,
колебательной системы (при δ = 0).
решение этого уравнения:
где:
хающих колебаний,
частота затухающих колебаний. Промежуток времени колебаний уменьшается в e раз называется временем релаксации. Затухание нарушает периодичность колебаний. Затухающие колебания не являются периодическими. Однако если затухание мало, то можно условно пользоваться понятием периода затухающих колебаний как промежутка времени между двумя последующими максимумами колеблющейся физической величины:
24. Декремент затухания. Если A (t) и A (t + T) — амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающихся на период, то отношение
называется декрементом затухания, а его логарифм
называется логарифмическим декрементом затухания. Здесь N — число колебаний, совершаемых за время уменьшения амплитуды в e раз. 25. Добротность колебательной системы. Добротностью колебательной системы называется безразмерная величина Q, равная произведению 2π на отношение энергии W (t) колебаний системы в произвольный момент времени t к убыли этой энергии за промежуток времени от t до t + T (за один условный период затухающих колебаний):
Энергия W (t) пропорциональна квадрату амплитуды A (t), поэтому:
При малых значениях логарифмического декремента затухания (
26. Примеры свободных затухающих колебаний Рассмотрим затухающие колебания различной физической природы: 1) механические колебания — пружинный маятник с массой m, который совершает малые колебания под действием упругой силы 2) электромагнитные колебания — колебания в колебательном контуре состоящем из сопротивления R, индуктивности L и емкости C Будем сравнивать оба случая с дифференциальным уравнением свободных затухающих колебаний линейной системы
решение которого имеет вид
27. Вынужденные колебания. Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X (t), изменяющегося по гармоническому закону:
В случае механических колебаний таким фактором является вынуждающая сила В случае электрического колебательного контура роль X (t) играет подводимая к контуру внешняя ЭДС или переменное напряжение
В общем виде дифференциальное уравнение вынужденных колебаний имеет вид
Это уравнение — линейное неоднородное дифференциальное уравнение. Его решение равно сумме общего решения уравнения и частного решения неоднородного уравнения. Можно показать, частное решение имеет вид
где A и Так для электромагнитных колебаний, если обозначить фазе между зарядом и приложенным напряжением, то можно показать, что решение дифференциального уравнения будет иметь вид q= где
Сила тока при установившихся колебаниях:
где
Силу тока можно записать в виде сдвиг по фазе между током и приложенным напряжением. Тогда можно показать, что
|


 − циклическая частота свободных незатухающих колебаний той же
− циклическая частота свободных незатухающих колебаний той же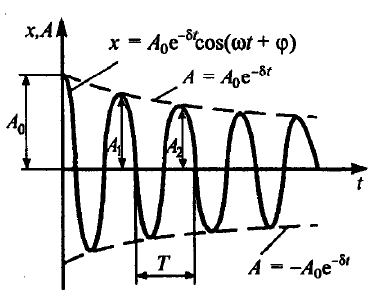 В случае малых затуханий (
В случае малых затуханий ( )
)
 — амплитуда зату-
— амплитуда зату- – начальная амплитуда,
– начальная амплитуда, — циклическая
— циклическая , в течение которого амплитуда затухающих
, в течение которого амплитуда затухающих
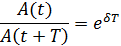



 <<1)
<<1) , поэтому (принимая
, поэтому (принимая  )
) 
 и силы трения
и силы трения  (r — коэффициент сопротивления)
(r — коэффициент сопротивления)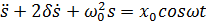
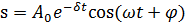







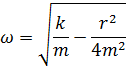






 t. Закон движения для пружинного маятника будет иметь вид
t. Закон движения для пружинного маятника будет иметь вид
 t. Уравнение колебаний в контуре будет иметь вид
t. Уравнение колебаний в контуре будет иметь вид

 задаются формулами
задаются формулами 

 — сдвиг по
— сдвиг по cos(
cos( ),
),