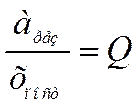Вынужденные колебания гармонического осциллятора.
где F0 - амплитудное значение действующей силы; w - частота вынуждающей силы.
где F1 - возвращающая сила, F = - kx; F2 - сила сопротивления, F = - rv (при малых значениях v); F3 - вынуждающая сила, F = F0×sinwt.
Неоднородное, линейное дифференциальное, второго порядка с постоянными коэффициентами. Общее решение неоднородного уравнения равно сумме общего решения однородного и частного решения неоднородного. ОН=ОО+ЧН
xo и jo – постоянные, определяющиеся начальными условиями
Найдем частное решение неоднородного дифференциального уравнения по виду правой части: x2=a cos(wt-j) a-? j-?
Частное решение неоднородного уравнения
А его общее решение будет таким:
С течением времени t e-bt®0 и первое слагаемое ®0 и общее решение становится равным второму слагаемому – установившиеся колебания
Анализ:
1. гармонические колебания происходят с частотой w равной частоте вынуждающей силы 2. амплитуда вынужденных колебаний зависит от амплитуды 3. параметров колебательной системы 4. и соотношение частот вынуждающей силы и собственной частоты 5. фаза вынужденных колебаний отстает от фазы вынуждающей силы на
Резонанс
а=j(w)
Анализируем знаменатель дроби на минимум:
((wо2-w2)2+4b2w2)¢=2(wо2-w2)2w+4b22w= =4w(wо2-w2)+8b2w=0
4w(wо2-w2 + 2b2)=0;
w=0 w2-(wo2-2b2)=0;
w=0 не имеет физического смысла
Нет смысла и у выражения
А вот выражение
Представляет собой точку максимума амплитуды вынужденных колебаний – резонанс
Если затухание в среде мало
Подставив в выражение для амплитуды вынужденных колебаний
резонансную частоту
Получим выражение для амплитуды колебаний при резонансе:
При При наличии затухания
добротности колебательной системы
|

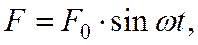
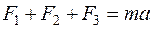 4
4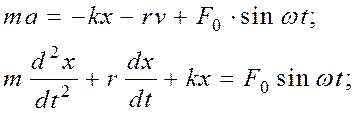
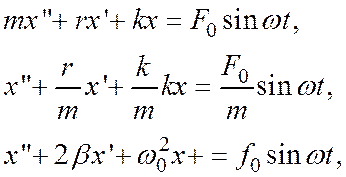
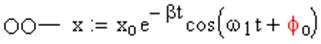
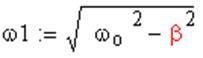
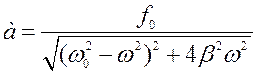
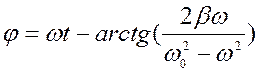
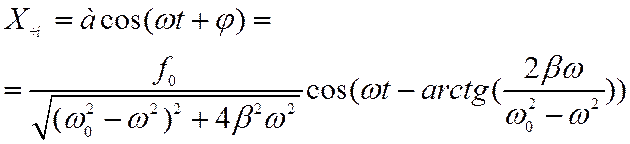

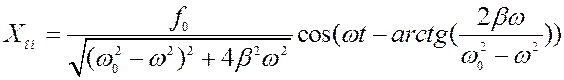
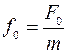 вынуждающей силы,
вынуждающей силы,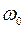 , свойств среды
, свойств среды 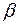 .
.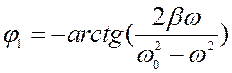
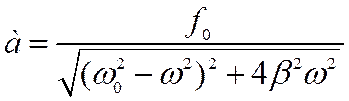
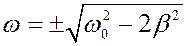
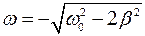
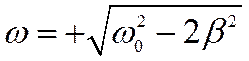
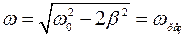
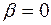 то
то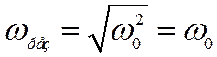
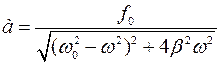
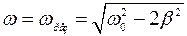
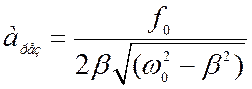
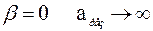 - нет физического смысла
- нет физического смысла