Барнаул 2006. Что такое электрический пробой?
Что такое электрический пробой? От каких факторов зависит пробой? Назовите стадии пробоя и их отличительные особенности? Чем обусловлена стохастичность пробоя? Назовите процессы ответственные за инициирование и развитие разряда? Какие неустойчивости приводят к развитию плазменных каналов? Чем характеризуется каждая из неустойчивостей? Что такое фрактал? Приведите примеры фрактальных структур? Что такое фрактальная размерность и как можно ее определить? Какими свойствами обладают фрактальные структуры?
Литература
1. Смирнов Б.М. Физика фрактальных кластеров. - М.: Наука, 1991. - 136 с. 2. Федер Е. Фракталы. - М.: Мир, 1991. - 254 с. 3. Сканави Г.И. Физика диэлектриков. (Область сильных полей). - М.: ГИФМ, 1958. - 907 с. 4. Бонч-Бруевич В.Л., Звягин И.П., Миронов А.Г. Доменная электрическая неустойчивость в полупроводниках. - М,: Наука, 1972. 5. Niemeyer L., Pietronero L., Wiesman H.J. Fractal dimension of dielectric breakdown. - Phys. Rev. Lett., 1984, vol. 52, p. 1033-1036. 6. Кухта В.Р., Лопатин В.В., Носков М.Д. Применение фрактальной модели к описанию развития разряда в конденсированных диэлектриках. - ЖТФ, 1995, т. 65, вып. 2, с.63-75.
Министерство образования и науки Российской Федерации Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. И.И.ПОЛЗУНОВА Кафедра «Электроснабжение промышленных предприятий» Фрактальная модель дендритообразования при пробое диэлектриков
Методические указания к лабораторной работе
Барнаул 2006 ВВЕДЕНИЕ
Твердые и жидкие диэлектрики широко используются в качестве изоляции в высоковольтных электрофизических устройствах и технологических установках. Пробой изоляции в процессе эксплуатации оборудования крайне нежелателен. Для прогнозирования пробоя необходимо знание причин, вызывающих снижение электрической прочности. Поэтому новые методы исследования, позволяющие выявить неизвестные грани явления пробоя или углубляющие наши знания об изучаемом процессе, являются актуальными. Применение теории фракталов для описания пробивных процессов является одним из методов их изучения. Электрический пробой - переход материала диэлектрика из непроводящего состояния в проводящее, сопровождающийся формированием плазменного канала, включает в себя множество процессов и зависит от многих факторов: материала диэлектрика и его свойств, вида и амплитуды воздействующего напряжения, материала электродов и их геометрии и т.д. Исследование пространственно-временных и электрических характеристик пробоя позволили разделить его во времени на три стадии: начальная стадия, стадия развития, Начальная стадия (в других терминах: статистическое время tст запаздывания начала развития канала разряда; инициирования развития разряда, "инкубационный" период накопления необратимых изменений в диэлектрике) сильно зависит от напряженности электрического поля, свойств диэлектрика и потенциального барьера на границе электрод-диэлектрик. Стадия развития разряда, в течение которой растут проводящие каналы и перекрывают весь промежуток. Длительность этой стадии формирования канала разряда tф зависит от соотношения максимальной локальной Еmax и средней Еср напряженностей электрического поля Еср=V/d где V - воздействующее напряжение, d - длина межэлектродного промежутка. В резконеоднородных полях, когда коэффициент неоднородности k=Еmax/Еср>102, длительность начальной стадии tст мала и время до пробоя определяется второй стадией. Канальная стадия, в течение которой в промежутке устанавливается дуга, завершающая пробой. В данной работе рассматривается только вторая стадия. Известно, что электрический пробой имеет случайный (стохастический) характер, т.к. tст и tф являются случайными (стохастичными) величинами. Структура каналов разряда, их расположение в пространстве стохастичны и не повторяются от опыта к опыту. Обусловлено это внутренней структурой диэлектрика и неустойчивостями в развивающихся плазменных каналах. Излучение стохастических структур, подобных развивающемуся каналу разряда, привлекательно проводить, используя методы физики фракталов. В работе приведены основные понятия фрактальной геометрии и их применение для описания структуры разряда. Рассмотрена фрактальная модель пробоя диэлектрика. Основные допущения модели: процессы, ответственные за развитие разряда, определяются только локальной напряженностью поля вблизи разрядных каналов. Компьютерное моделирование процессе роста каналов разряда позволяет получить наглядное представление пробоя в диэлектрике.
1. ПРЕДПРОБИВНЫЕ ПРОЦЕССЫ В КОНДЕНСИРОВАННЫХ ДИЭЛЕКТРИКАХ
Основным процессом, ответственным за инициирование и развитие разряда в диэлектриках, является генерация и перенос носителей зарядов в сильных электрических полях. Генерация электронов, дырок и ионов осуществляется из электродов за счет авто электронной и термоавтоэлектронной эмиссии. Носители зарядов образуются и в самом диэлектрике за счет диссоциации молекул, ударной или электростатической ионизации собственных и примесных состояний диэлектрика. Взаимодействие носителей заряда с веществом сопровождается формированием неустойчивостей, приводящих к инициированию и развитию плазменных каналов. Можно выделить несколько типов таких неустойчивостей: тепловая, электромеханическая, электрополевая, токовая и ионизационная.
1.1. Тепловая неустойчивость Это наиболее универсальный тип неустойчивости. Она возникает в диэлектриках с большой проводимостью s и сильным ее возрастанием с увеличением температуры, например, для активационной зависимости s(T) = s0exp (W/kT) (1.1) где W - энергия активации проводимости, k - постоянная Больцмана, T - температура в градусах Кельвина. При приложении напряжения диэлектрик разогревается токами проводимости. Неоднородность реальных диэлектриков вызывает появление зон с интенсивным и умеренным тепловыделением. Рост температуры увеличивает проводимость локальных областей. В этих областях будет происходить шнурование тока, интенсивный разогрев и фазовый переход, который может быть обусловлен проплавлением, разрушением или ионизацией "разогретыми" в электрическом поле носителями заряда. Напряженность поля, при которой развивается тепловая неустойчивость определяется из баланса энергии
где g, c - удельная плотность и теплоемкость материала, t - время действия электрического поля. Тепловая неустойчивость используется в различных теориях теплового пробоя твердых диэлектриков.
1.2. Электромеханическая неустойчивость Электромеханические (пандеромоторные) силы электрического поля создают давления на диэлектрик
где e и e¥ - относительные диэлектрические проницаемости для частоты воздействующего напряжения и оптического диапазона, E - локальная напряженность поля. Возникающие при этом механические напряжения недостаточны для разрушения диэлектриков. С учетом дефектов на границе электрод-диэлектрик может оказаться достаточным для разрушения давление P~2×107 н/м2. Давление необходимое для разрушения может быть достигнуто у устья микротрещин, образующихся в объеме твердых диэлектриков. Электромеханическая неустойчивость может увеличиться за счет инжекции в диэлектрике объемного заряда. Электрическое поле, действуя на заряд плотностью r, создает дополнительную локальную силу F =rE (1.4) Жидкие диэлектрики под действием этой силы приходят в электро-гидродинамическое движение (ЭГД-течение). Кулоновское расталкивание зарядов одного знака в зоне объемного заряда создает натяжение в жидкости (пониженное давление) и жидкость "вскипает". Кулоновское натяжение и ЭГД-течение вызывает кавитацию с образованием микропузырьков. Ионизация в микропузырьках приводит к инициированию разряда.
1.3. Электрополевая и токовая неустойчивость Инжекция зарядов в полупроводники и диэлектрики становится заметной уже при Е³104 В/см. В сильных полях, даже если нагрев незначителен, диэлектрики обладают значительной проводимостью, обусловленной, как правило, движением холодных электронов в зоне проводимости или дырок в валентной зоне, т.е. в сильных полях в твердых диэлектриках образуется низкоэнергетическая электрон-дырочная плазма низкой плотности. Разогрев носителей заряда в сильных полях, благодаря сильной зависимости подвижности носителей заряда m и их концентрации n от напряженности поля, часто вызывает появление отрицательной дифференциальной проводимости с S или N - образными вольт-амперными характеристиками. Системы с отрицательной дифференциальной проводимостью неустойчивы относительно продольных и поперечных флуктуаций тока и напряженности поля. Продольные флуктуации приводят к образованию доменов (областей сильного поля, способных пробиться внутри), а поперечные - к шнурованию тока вдоль силовых линий, увеличению плотности носителей заряда и образованию плазменных каналов. Заметим, что для образования плазменных каналов по такому механизму неустойчивости первичным электронам (дыркам) необязательно иметь энергию, достаточную для ионизации атомов среды. Теория полевой и токовой неустойчивости были созданы для описания пробоя полупроводниковых структур и хорошо описывают пробой "плохих" диэлектриков с проводимостью s³10-10 Ом-1 см-1.
1.4. Ионизационная неустойчивость В сильных электрических полях, когда tст мало, плазменные каналы могут образовываться за счет ударной и электростатической ионизации. Генерация носителей заряда за счет электростатической ионизации маловероятна даже при пробивных напряженностях для твердых диэлектриков (Eпр<107 В/см). Более вероятна ударная ионизация. Если предположить линейную зависимость скорости электрона v от напряженности электрического поля Е v=mE (1.5) где m - подвижность электрона, то напряженность поля необходимую для ускорения электрона до энергии, равной потенциалу ионизации ui можно определить из условия:
Отсюда напряженность поля необходимая для ударной ионизации
Для реальных диэлектриков ui£10 эВ; подвижнось заряженных частиц, электронов, дырок Ионизационной неустойчивостью завершается любой механизм развития разряда, поскольку он обязательно должен завершиться образованием плазменных каналов и перемыканием ими межэлектродного промежутка. При выборе механизма пробоя всегда трудно ответить, где происходит ионизация, насколько возмущен другими неустойчивостями ионизуемый диэлектрик. Анализируя оценки величины E, достаточной для возникновения неустойчивостей, можно сделать следующие выводы. Во-первых, пробивной напряженности поля Eпр=105¸107 В/см реальных диэлектриков недостаточно для развития какой-либо отдельной неустойчивости и перемыкания плазменными каналами промежутка. Во-вторых, развитие любого вида неустойчивости стохастично во времени и пространстве и зависит от локальной напряженности поля Eл. Величина Eл может изменяться как вследствие одновременности развития нескольких неустойчивостей (например, ионизация происходит в кавитационных пузырьках, в низкотемпературной электронно-дырочной плазме и др.), так и благодаря наличию в реальных диэлектриках и на электродах "слабых мест", облегчающих возникновение неустойчивостей. Такими "слабыми местами" являются трещины, пузырьки газа, микровключения неосновных фаз и др. подобные нарушения.
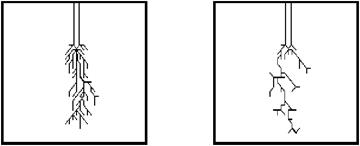
1.5. Описание развития разряда в диэлектрике Стадия развития разряда сопровождается существенными изменениями диэлектрических свойств материала. Неустойчивости любого вида преобразуются в конце концов в ионизационную. Ионизационные плазменные каналы, распространяясь случайным образом в диэлектрике, формируют структуру будущего канала пробоя. Форма разрядной структуры может быть кустообразной или древовидной. Развитие светящихся ионизационных каналов начинается при определенной для каждого диэлектрика напряженности поля Е. Вид разрядных структур и их динамика во всех жидких и твердых диэлектриках подобны. Исключения составляют некоторые кристаллические тела, в которых наблюдается преимущественная кристаллографическая направленность развития каналов. В процессе развития разрядные каналы испытывают случайные изгибы, ветвления и остановки в развитии. Диаметр каналов составляет от единиц до ста микрон. Пространственно-временные характеристики разрядных структур зависят от параметров плазмы в разрядных каналах и локальной напряженности поля Ел на головке канала. Ел может снизиться вследствие экранирования поля соседними каналами при их большом числе и из-за падения напряжения DV на длине канала при конечной плотности зарядов n и проводимости s плазмы. Аппроксимируя канал параболоидом вращения, напряженность поля на головке канала при r0<<d можно рассчитать Е =2(V0-DV)/r0 (ln 4d/r0), (1.8) где V0 - приложенное напряжение, r0 - радиус канала, d - длина межэлектродного промежутка, DV - падение напряжения на канале, DV=Ekl (l - длина канала). Напряженность поля внутри канала
где jk - плотность тока в канале, sk - проводимость канала. Даже если проводимость плазмы постоянна, то по мере роста канала DV увеличивается, а Eл снижается, и развитие разрядной структуры может прекратиться. К уменьшению скорости развития и остановке разрядной структуры может также привести одновременное развитие большого числа каналов, которые выравнивают распределение поля, уменьшая коэффициент неоднородности поля k=Е л/Еср. Флуктуация проводимости и диаметра каналов вызывают неоднородность распределения заряда на их поверхности и, соответственно, неоднородность распределения поля по длине каналов. Это приводит к ветвлению и изгибам развивающихся каналов. Выше упоминалось, что каналы формируются, когда достигается критическая напряженность поля Ес. Тогда вероятность пробоя отдельных участков диэлектрика или всего промежутка можно аппроксимировать как P(E)~Eh. Показатель h можно рассчитать методом квантовой механики или статистической физики по какому-либо конкретному механизму разрушения диэлектрика. Оценить величину h, в первом приближении можно из предположения, что пробой диэлектрика наступает, когда выделяемая в единице объема диэлектрика энергия достаточна для его разрушения. Вероятность пробоя тогда пропорциональна выделяемой энергии P(E) ~ W. Энергия, выделяемая в единице объема при распространении каналов, пропорциональна запасаемой в диэлектрике энергии W~0,5ee0E с2, то есть P(E)~Eс2. Поэтому в первом приближении можно принять h=2. Развитие разрядных структур - стохастический процесс и подчиняется статистическим закономерностям. Стохастичность обусловлена как флуктуациями параметров плазмы в каналах, так и флуктуациями состояния диэлектрика. Для исследований свойств стохастических разрядных структур и их количественного описания можно использовать методы физики фракталов и компьютерное моделирование процесса роста структур.
2. ОСНОВЫ ФРАКТАЛЬНОГО ПОДХОДА
Изучая различные встречающиеся в природе явления и объекты, мы прежде всего описываем их геометрическую форму. При этом обычно используем понятия евклидовой геометрии: прямые, плоскости, окружности, сферы и т.д. Однако многие процессы, протекающие в природе, приводят к образованию структур, для описания которых недостаточно обычной геометрии. Возьмем примеры из природы: форма гор, рек, береговых линий, облаков, деревьев. Их сложно описать с помошью прямых линий, плоскостей, сфер и т.д. Отличительной особенностью этих объектов является самоподобие, т.е. часть объекта подобна целому. Например, геометрия притока реки подобна геометрии всей реки. Рассматривая самоподобный объект во все увеличивающихся масштабах, мы будем выявлять все более тонкие детали его структуры, а вновь выявленная структура будет подобна той, что можно видеть в более мелком масштабе. Обладающие такими свойствами объекты называют фракталами. (Термин "фрактал" от латинского слова "fractus" - изломанный был введен в науку в 1975 г. Б. Мандельбратом). В последние годы понятие фрактал стало широко распространенным в разных областях науки: в физике, химии, биологии, социологии и т.д. Фрактальные свойства обнаружены у множества объектов. Молекулы белков и скопление звезд в космосе, структуры кровеносных сосудов человека и поверхности разломов стали, турбулентные течения и электрические разряды и т.д. - все эти различные по своей природе структуры обладают фрактальными свойствами. Мы определили фрактал, как структуру которая состоит из частей, которые в каком-то смысле подобны целому. Количественно фрактальная структура характеризуется значением своей фрактальной размерности. Определим понятие фрактальной размерности, как размерности подобия. Рассмотрим, в качестве примера, одномерный объект - отрезок
а) б) Рис. 2.1 Если мы будем разбивать на части двумерный объект - квадрат, то увидим, что он состоит из N2 своих копий уменьшенных в N раз (рис. 2.2). Трехмерный куб состоит уже из N3 своих копий уменьшенных в N раз (2.3). Таким образом, если D мерный объект состоит из К(N) своих копий уменьшенных в N раз, то выполняется соотношение K(N)=ND (2.1)
Рис. 2.2 Рис. 2.3
Из этого соотношения можно выразить размерность объекта
Теперь попытаемся построить объект, имеющий дробную размерность. Построение будем проводить по шагам. Пусть на нулевом шаге n=0 имеется отрезок АВ длиной L0 (рис. 2.4, а). На первом шаге заменяем исходный отрезок тремя отрезками длины L1=L0/2, расположенными друг относительно друга, как показано на рис. 2.4, б. На втором шаге, каждый из новых отрезков длиной L1 заменяем тремя отрезками длиной L2=L1/2 (рис. 2.4, в). Аналогичным образом выполняются третий и четвертый шаги (рис. 2.4, г, д). Мысленно, продолжая описанную процедуру до бесконечности, получим самоподобный объект, который состоит из трех своих копий уменьшенных в два раза. Следовательно, ему можно сопоставить дробную размерность D равную ln 3/ ln 2 ~ 1,585. Построенный таким образом объект является геометрическим фракталом. Так же как и любой объект геометрии, он "идеализирует" действительность. Реальные же физические фрактальные объекты, такие, например, как фрактальные кластеры (агрегаты, образующиеся при слипании микроскопических частиц), являются самоподобными только статистически. К тому же они всегда имеют некоторый минимальный размер (в случае фрактального кластера - это размер частиц, из которых он состоит) и максимальный размер. Поэтому, можно говорить о фрактальности реальных объектов только в определенном диапазоне масштабов: от минимального до максимального.
а) б) в) г) д) Рис. 2.4
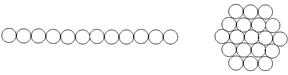
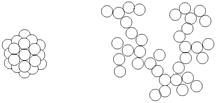
Фрактальные структуры обладают очень важным, с точки зрения физики, свойствами. Чтобы лучше его понять рассмотрим, сначала, одномерную структуру, например, линейную цепочку микрочастиц длиной l (рис. 2.5). Очевидно, что число частиц в таком объекте n пропорционально размеру l (n~l). Если частицы образуют двумерный объект - диск (рис. 2.6), то n~l2. Для трехмерного объекта n~l3 (рис. 2.7). Можно сказать, что для фрактальной структуры (рис. 2.8) с дробной размерностью D выполняется соотношение n~lD (2.3) Следовательно, число элементов из которых состоит фрактал пропорционально его размеру в степени D, где D - фрактальная размерность объекта.
Рис. 2.5 Рис. 2.6
Рис. 2.7 Рис. 2.8
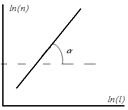
Рассмотренное свойство лежит в основе широко используемого экспериментального метода определения фрактальной размерности. Чтобы определить размерность фрактальной структуры, необходимо построить в двойном логарифмическом масштабе график зависимости числа элементов, составляющих фрактал, от его размера l. Полученная зависимость аппроксимируется прямой линией, тангенс угла наклона которой и будет равен фрактальной размерности (рис. 2.9): D=tga (2.4) Таким образом, мы ввели понятие фрактала, дали определение фрактальной размерности D, рассмотрели метод ее вычисления. Все это составляет геометрическую основу
Рис. 2. 9 фрактального подхода к изучению различных физических явлений. Физика фракталов изучает связь между фрактальной геометрией и физическими свойствами природных явлений. При этом можно выделить два основных направления исследований. Первое связано с ответом на вопрос, как фрактальные структуры возникают в природе. Второе направление изучает какими особенными физическими свойствами обладают различные фрактальные структуры. Мы будем применять методы физики фракталов для изучения структуры разрядных каналов возникающих при пробое диэлектрика. С помощью понятий фрактальной геометрии можно не только качественно, но и количественно описать возникающие на второй стадии пробоя стохастические структуры разрядных каналов, подобные изображеным на рис. 1.1-1.3. Кустообразная структура, рис. 1.1, плотно заполняет пространство, т.е. можно сказать, что она имеет размерность равную трем и, следовательно, не является фракталом. В отличие от нее древовидная структура, рис. 1.2, самоподобна и обладает фрактальными свойствами. Фрактальную размерность D такой структуры можно определить, используя вытекающее из формулы (2.4) соотношение между полной длиной L(r) всех разрядных каналов, заключенных в сфере радиуса r с центром в начале структуры, и величиной r, L(r)µrD (2.5) Из выражения (2.5) следует, что фрактальная размерность D будет равна тангенсу угла наклона прямой, аппроксимирующей график зависимости ln L от ln r. Измеренная таким способом фрактальная размерность D структуры, изображенной на рис. 1.2, равна примерно 1,8. Фрактальная размерность развивающихся при пробое разрядных структур зависит от свойств диэлектрика и вида прикладываемого напряжения. Например, анализ экспериментальных данных показывает, что величина фрактальной размерности увеличивается с повышением напряжения. Следовательно фрактальная размерность разрядной структуры связана с происходящими при пробое процессами. Поэтому определение фрактальной размерности имеет важное значение для полного понимания физики пробоя диэлектриков.
3. КОМПЬЮТЕРНАЯ МОДЕЛЬ РОСТА РАЗРЯДНОЙ СТРУКТУРЫ
3.1. Возможности компьютерного моделирования В последние годы, благодаря широкому распространению персональных компьютеров и появления суперкомпьютеров, вычислительные методы получают все более широкое распространение в физике. Компьютерное моделирование позволяет решать сложные задачи, не поддающиеся решению иными методами. Для изучения формирования пробоя диэлектриков кампьютерные эксперименты имеют особое значение, как в виду сложности образующихся разрядных структур, так и вследствие несовершенства теоретических моделей их роста. Чтобы глубже понять природу сложного физического процесса, часто бывает полезно отвлечься от учета всех деталей явления и рассматривать достаточно простую модель, которая воспроизводит основные свойства процесса. Поэтому мы будем рассматривать модель пробоя диэлектрика, основанную на простом алгоритме роста и содержащую всего несколько параметров. Однако уже такая модель приводит к реалистичным структурам разряда, позволяет проводить их анализ и сравнение с результатами эксперимента. Параметры модели имеют наглядную физическую интерпретацию, и варьируя их значения можно изменять характер роста разряда.
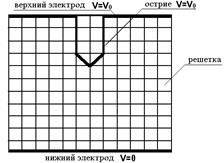
3.2. Общая структура модели разряда Развитие разряда в реальном диэлектрике является случайным процессом. Причиной этому могут служить как стохастические изменения величины тока в каналах разряда, так и флуктуации состояния диэлектрика. Поэтому, мы будем рассматривать стохастическую модель развития разряда. Исходя из практического интереса, выберем геометрию разрядного промежутка в виде острие-плоскость (рис. 3.1). Хотя большинство реальных разрядов происходит в объеме, мы в целях простоты и наглядности, а также из-за ограниченных вычислительных возможностей имеющихся компьютеров, будем рассматривать двухмерную модель разряда. Компьютерное моделирование удобней проводить в дискретном пространстве. Геометрия электродов используемая для моделирования
Рис. 3.1 Поэтому представим пространство между электродами в виде квадратной решетки, каждый узел которой может относиться к диэлектрику или к структуре разряда (рис. 3.1). Узлы диэлектрика, которые стали принадлежать структуре разряда, будем называть пробитыми. Начальное распределение потенциала зададим следующим образом. Верхний электрод с острием имеет потенциал V0, а нижний электрод находится под нулевым потенциалом. Значение потенциалов в узлах решетки определяются по граничным условиям с помощью теремы Гаусса:
где
разряда на решетке Рис. 3.2 Рост структуры разряда начинается с острия и происходит по шагам. За один шаг структура растет или на одно ребро, или на одну диагональ решетки. На рис. 3.2 изображена примерная конфигурация разряда после нескольких шагов. Черные кружки отмечают узлы, принадлежащие структуре разряда - пробитые узлы. Крестиками отмечены узлы, которые могут быть пробиты на следующем шаге. Вероятность того, что пробой произойдет по некоторому ребру или диагонали, соединяющей уже принадлежащий структуре разряда и еще не пробитый узел, зависит от локальной напряженности поля между ними (разности потенциалов между этими узлами деленной на расстояние между ними). В настоящей модели вероятность пробоя в рассматриваемой точке принимается пропорциональной напряженности поля Е в степени h, если локальная напряженность поля Е больше некоторой критической напряженности Ес, в противном случае равна нулю: Значение параметра роста h и величина Ес зависят от свойств диэлектрика и происходящих при пробое процессов, а стохастичность модели заключается в том, что из полученного распределения вероятности роста (3.2), случайным образом выбирается направление роста на данном шаге. Поскольку структура разряда обладает большей электрической проводимостью, чем диэлектрик, то ее развитие будет приводить к выносу заряда в межэлектродное пространство и изменению распределения поля в диэлектрике. В данной модели изменение распределения плотности свободных зарядов в структуре разряда определяются исходя из закона Ома j=gE и уравнения непрерывности:
В процессе развития пробоя проводимость структуры пробоя меняется. Ионизация, джоулево нагревание, процессы расширения каналов ведут к увеличению проводимости. Напротив, рекомбинация, охлаждение излучением и ударными волнами уменьшают проводимость. Поэтому в настоящей модели увеличение проводимости связывается с освобождаемой в каналах энергией, а уменьшение ее считается прямо пропорциональной самой себе:
Важным аспектом развития структуры разряда является зарождение канала. В настоящей модели допускается, что если канал инициируется с поверхности острия, то его проводимость равна некоторой начальной проводимости. Другое правило используется для распространения каналов. Проводимость вновь образовавшегося канала gnew пропорциональна проводимости старого канала gold, из которого растет новый: gnew=lgold (3.5) где l - коэффициент передачи проводимости Для того, чтобы адекватно описывать динамику переноса энергии и движения зарядов, было введено физическое время. Поскольку рост структуры разряда в настоящей модели определяется распределением вероятности роста (3.2), то необходимо учитывать его и при переходе к физическому времени. Из уравнения (3.2) следует, что функция скорости роста w(Е) в любой точке структуры разряда имеет степенную зависимость от напряженности поля w(Е)=Еh/q, где q - некоторая постоянная. Так как события роста структуры разряда в разных точках статистически независимы, полная функция скорости W есть сумма w(Е) по всем возможным направлениям роста: W=åw(Е). Среднее время роста канала Dt обратно пропорционально W: Dt=1/W. Поэтому: Dt = (åw(E))-1 = q/åEh = q/Z (3.6) Таким образом, после каждого шага роста необходимо вычислять новые значения потенциала во всех узлах, принадлежащих диэлектрику согласно новым граничным условиям. Граничными условиями будут значения потенциала электродов и плотность свободных зарядов узлов, принадлежащих структуре разряда.
3.3. Расчет распределения плотности свободных зарядов Изменение распределения плотности зарядов Dri,j в структуре разряда определяется из уравнения (3.3) в дискретной форме после каждого шага роста:
Изменение проводимости структуры разряда Dg (n)i,j рассчитывается на каждом шаге роста из (3.4) в дискретном виде:
Вне структуры разряда проводимость диэлектрика принимается равной нулю. Интервал физического времени Dt(n) для n-ого шага роста определяется из (3.6) в дискретном виде: Dt(n)=q/Z(n) (3.9) 3.4. Расчет электрического потенциала внутри диэлектрика Расчет потенциала Фi,j по решетки
Рис. 3.3 Фi,j - потенциал в узле с координатами i,j. В настоящей модели значение потенциалов на узлах решетки, моделирующей диэлектрик, Фi,j будут удовлетворять дискретному аналогу уравнения Пуассона (рис. 3.3).
Найти решения уравнения (3.10) с заданными граничными условиями можно, используя метод итераций. Суть его заключается в том, что исходя из какого-либо начального распределения потенциала Ф(0)i,j- нулевого приближения, не удовлетворяющего уравнению Пуассона, построить первое приближение Ф(1)i,j по формуле (3.10). Затем по первому приближению Ф(1)i,j построить второе Ф(2)i,j и т.д. Итерации нужно производить до тех пор, пока разница между последующими приближениями не станет меньше некоторой наперед заданной величины, зависящей от требуемой точности расчета. Таким образом можно получить решение уравнения Пуассона с любой наперед заданной точностью. В настоящей работе такой расчет поля производится после каждого шага роста структуры разряда с точностью 1%.
3.5. Расчет вероятности роста структуры разряда Вероятность роста структуры разряда в том или ином месте может зависеть от локальной напряженности поля, так и от состояния диэлектрика. Имеющиеся в настоящее время данные не позволяют точно определить эту вероятность. Поэтому мы выберем простой и в то же время достаточно общий вид зависимости вероятности Р(i,j)(l,m) пробоя между узлами с координатами (i, j) и (l, m) от напряженности поля Е(i,j)(l,m) между ними. Напомним, что напряженность поля между узлами вычисляется через потенциалы узлов Фi,j и расстояние r(i,j)(l,m) между узлами
Если локальная напряженность поля больше или равна некоторой критической Еc, то вероятность Р(i,j)(l,m) присоединения нового элемента с координатами l,m к уже имеющейся структуре разряда (пробой между узлами (i,j) и (l,m) решетки) предположим пропорциональной значению локальной напряженности поля Е(i,j)(l,m) в степени h. В противном случае, когда локальная напряженность поля меньше критической, вероятность будет равна нулю. То есть
Здесь Z нормировочный множитель. Из условия нормировки вероятности
получим:
Суммирование в формулах (3.13) и (3.14) ведется по всем парам узлов, между которыми возможен пробой. Таким образом, в настоящей модели зависимость вероятности пробоя от локальной напряженности включает два параметра: критическую напряженность поля Еc и показатель роста h. Значения обоих параметров зависят от свойств диэлектрика, пробой которого мы моделируем. Рассмотрим влияние этих параметров на характер роста структуры разряда. Увеличение значения критической напряженности Еc приводит к уменьшению возможных путей роста и, следовательно, к уменьшению степени ветвления структуры разряда. Если критическая напряженность Еc превосходит локальную напряженность во всех точках, то развитие разряда прекращается, и мы имеем незавершенный пробой. Параметр h определяет степень зависимости роста от величины локальной напряженности поля.
Результат моделирования Результат моделирования при h= 1 при h= 2
Рис. 3.4 Рис. 3.5 При h=0 рост равновероятен для всех разрешенных направлений. В результате будет образовываться плотная структура, полностью заполняющая пространство. При больших значениях параметра h (h >>1) рост будет происходить только в напра
|

 (1.2)
(1.2) (1.3)
(1.3)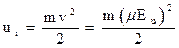 (1.6)
(1.6)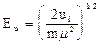 (1.7)
(1.7)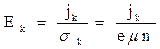 (1.9)
(1.9)

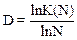 (2.2)
(2.2)
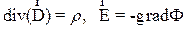 (3.1)
(3.1)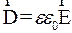 - вектор электрической индукции, Ф - электрический потенциал, r - плотность свободных зарядов, e - относительная диэлектрическая проницаемость, e0 - абсолютная диэлектрическая проницаемость.
- вектор электрической индукции, Ф - электрический потенциал, r - плотность свободных зарядов, e - относительная диэлектрическая проницаемость, e0 - абсолютная диэлектрическая проницаемость.
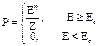 (3.2)
(3.2)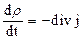 (3.3)
(3.3)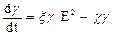 (3.4)
(3.4) (3.7)
(3.7)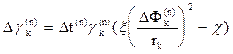 (3.8)
(3.8)
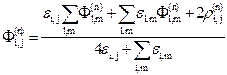 (3.10)
(3.10) (3.11)
(3.11)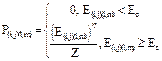 (3.12)
(3.12)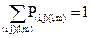 (3.13)
(3.13) (3.14)
(3.14)