Кинематический раcчет
Кинематический раcчет Кинематическая схема представлена на рис.1
Рисунок 1- Кинематическая схема привода 1.1 Определяем общей КПД редуктора по формуле: h = hпкn·ηр, (1)
где hпк - КПД учитывающий потери на трение в одной паре подшипников качения; n – число пар подшипников в редукторе. ηр –КПД редуктора,. По таблице 1.2.1.[1] выбираем, hр =0,98 и hпк = 0,99 После подстановки получим:
h = 0,98∙0,992=0,96
1.2 Определяем требуемую мощность электродвигателя по формуле: Pтр= где P2– мощность на выходном валу привода (по заданию P2=7,6 кВт); h- КПД привода. После подстановки получим:
1.3 Исходя из условия (3) по таблице 16.7.1 [1] выбираем асинхронный электродвигатель Pдв ³ Pтр, (3)
с синхронной частотой вращения n = 1500 об/мин и коэффициентом скольжения 2,8% Частота вращения двигателя nдв =1500-1500·0,028=1458 (об/мин)
1.4 Определяем передаточное число редуктора по формуле: u= где nдв- частота вращения электродвигателя; n2 – частота вращения ведомого вала привода. После подстановки получим: u = 1.5 Определяем угловые скорости ведущего и ведомого валов: w= После подстановки получим: ω1 = ωдв= ω2 = Определяем частоту вращения каждого вала: n1= nдв=1458(об/мин), n2= 1.6 Определяем вращающие моменты на валах редуктора по формулам: Т1=Tдв=
T2=Т1 uрhпк·ηр =52·103·4,17·0,99·0,98=210∙103(Н∙мм)
Результаты расчета для наглядности представим в табличном виде (таблица 1)
Примем для шестерни и колеса разные марки стали, но одинаковые виды термообработки. По таблице 3.3 [2] примем для шестерни Сталь 45 улучшенную с твердостью HB 230, для колеса Сталь 45 улучшенную с твердостью HB 200. 2.1 Определим предельно допустимые напряжения: [σн]= где σhlimb – предел контактной выносливости при базовом числе циклов определяемый по формуле (8); KHl коэффициент долговечности; Sн - коэффициент запаса. σHlimb=2HB+70. (8) При длительной эксплуатации коэффициент долговечности KHl =1; коэффициент запаса Sн =1,2. После подстановки получим: [σн1] = [σн2] = Расчетное допускаемое напряжение определим по формуле: [σн]=0,45∙([σн1]+ [σн2]) (9) После подстановки получим: [σн]=0,45∙(482+428)=410 (МПа) Проверка [σн] £1,23[σн2] 410(МПа)£526(МПа) Условие выполнено. 2.2 Опредедяем межосевое расстояние по формуле: аω =ka∙(u+1)∙ где Т2- вращающий момент на ведомом валу; при симметричном расположении колеса относительно опор коэффициент KHb=1,15; u – передаточное число; [σн] – предельно допустимое напряжение; yba- коэффициент ширины венца по отношению к межосевому расстоянию. По рекомендациям ГОСТ 2185-65; ybа=0,5; для косозубых колес kа=43. После подстановки получим: аω =43∙(4,17+1)∙
2.3 Нормальный модуль зацепления определим по формуле: mn=(0,01…0,02) аω. (11) После подстановки получим: mn=(0,01…0,02)∙125= 1,25…2,5(мм) По ГОСТ 9563-60 принимаем mn=2 (мм) 2.4 Принимаем угол наклона зубьев β=30º. Определим числа зубьев шестерни и колеса по формулам: z1= z2= z1∙u. (13) После подстановки для шестерни и колеса соответственно получим: z1= Тогда принимаем z1=21. z2= 21∙4,17=87,57 Принимаем z2=88. Уточняем передаточное число u =88/21=4,19
Допускается до 2,5%.
2.5 Уточним угол наклона зубьев β по формуле: cosβ= После подстановки получим: cosβ= Угол β=29,3081º 2.6 Основные размеры зубчатой пары: Определим делительные диаметры по формуле: d= После подстановки для шестерни и колеса соответственно получим: d1=
Проверим межосевое расстояние по формуле: аω = После подстановки получим: аω= Определим внешние диаметры окружности вершин зубьев шестерни и колеса по формуле: da=d+2mn. (17) После подстановки для шестерни и колеса соответственно получим: da1=48,2+2∙2=52,2 (мм) da2=201,8+2∙2=205,8 (мм) Определим диаметры впадин зубьев: df =d-2,4mn df1 =48,2-2,4·2=43,4(мм) df2=201,8-2,4·2=197(мм)
Ширину колеса и шестерни определим по формуле: b2=ψba· aω; (18) b1=b2+5 (мм.) (19) После подстановки получим: b2=0,5·125=62,5 (мм) Принимаем b2=65мм b1=65+5=70 (мм) Коэффициент ширины шестерни по отношению к диаметру определим по формуле: ybd= После подстановки получим: ybd= Среднюю окружную скорость определим по формуле: ν= После подстановки получим: ν = При такой скорости для косозубых колес назначают 8-ю степень точности. 2.7 Проверим допустимое контактное напряжение, для этого по формуле определим коэффициент нагрузки: KH=KHb∙KHa∙KHn, (22)
по таблице 3.4[2] при 8-й степени точности и n£5 м/с KHa=1,07; при НВ<350 и n£5 м/с KHn=1,0. После подстановки получим: KH=1,07∙1,05∙1=1,12 Проверяем допустимое контактное напряжение по формуле: σH= После подстановки получим: σH=
Условие прочности выполнено. 2.8 Силы, действующие в зацеплении, определим по формулам: окружную: Ft= радиальную: Fr=Ft∙ осевую: Fа= Fr∙tgα. (26) После подстановки получим: Ft= Fr= Осевая сила в шевронных колесах Fа=0 (H), т.к. осевые силы, действующие на каждую половину шеврона, уравновешиваются.
2.9 Проверим зубья на выносливость по напряжениям изгиба по формуле: σF= где - KF- коэффициент нагрузки,определяем по формуле: KF=KFb∙KF v , (28)
По таблице 3.8 при твердости HB<350, скорости n=3,7 м/с и 8-й степени точности получим KF v =1,3. После подстановки получим: KF=1,13∙1,3=1,47 YF- коэффициент формы зуба, выбираемый в зависимости от эквивалентных чисел зубьев, определяемых по формуле: zν1= После подстановки для шестерни и колеса соответственно получим: zν1= zν2= Эквивалентные числа зубьев соответственно равны YF=3,7, YF=3,6. Коэффициент Yβ определим по формуле: Yβ=1- После подстановки получим: Yβ=1- Коэффициент КFα определим по формуле: КFα= где - коэффициент торцового перекрытия εа=1,5; n-степень точности торцового покрытия колеса. После подстановки получим: КFα = Допускаемые напряжения при проверке иHBjljkljghgkjjktt
зубьев на выносливость по напряжениям изгиба определим по формуле: [σF]= где по таблице 3.9 для Стали 45 нормализованной при твердости HB<350, s°Flimb=1,8 HB. После подстановки для шестерни и колеса соответственно получим:
s°Flimb2=1,8∙200=360 (МПа) Коэффициент запаса [SF] определим оп формуле: [SF]=[SF]¢∙[SF]¢¢; (33) где [SF]¢- коэффициент учитывающий нестабильность свойств материала зубчатых колес [SF]¢=1,75; [SF]¢¢- коэффициент, учитывающий способ получения заготовок для зубчатых колес. Для поковок и штамповок [SF]¢¢=1,0. После подстановки получим: [SF]=1,75∙1,0=1,75 После подстановки данных в формулу (32) получим: [σF1]= [σF2]= Найдем отношение [σF]/ YF соответственно для шестерни и колеса:
|


 , (2)
, (2) Pтр =
Pтр = 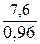 =7,92 (кВт)
=7,92 (кВт) Этому условию удовлетворяет электродвигатель марки 4А132М4У3 по ГОСТ 28330-90 с параметрами: мощностью Pдв = 11,0 кВт,
Этому условию удовлетворяет электродвигатель марки 4А132М4У3 по ГОСТ 28330-90 с параметрами: мощностью Pдв = 11,0 кВт, , (4)
, (4) = 4,17
= 4,17 , (5)
, (5) (рад/с),
(рад/с), =36,5 (рад/с),
=36,5 (рад/с), =350(об/мин).
=350(об/мин). =
=  = 52(Н·м)=52·103(Н·мм) (6)
= 52(Н·м)=52·103(Н·мм) (6) Таблица 1- Кинематические характеристики редуктора
Таблица 1- Кинематические характеристики редуктора 2 Расчет зубчатой передачи
2 Расчет зубчатой передачи , (7)
, (7) =482 (МПа)
=482 (МПа) =428 (МПа)
=428 (МПа) , (10)
, (10)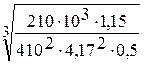 =122(мм)
=122(мм) Принимаем аω =125 (мм)
Принимаем аω =125 (мм)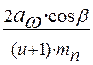 ; (12)
; (12) =20,94
=20,94
 . (14)
. (14) =0,872
=0,872 ∙z. (15)
∙z. (15)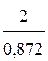 ∙21=48,2(мм)
∙21=48,2(мм) d2=
d2=  ∙88=201,8 (мм)
∙88=201,8 (мм) . (16)
. (16) =125 (мм)
=125 (мм) . (20)
. (20) =1,45
=1,45 (21)
(21) =3,7(м/с)
=3,7(м/с) где по таблице 3.5[2] при ybd=1,45симметричном расположении колеса и твердости HB<350 принимаем KHb=1,05;
где по таблице 3.5[2] при ybd=1,45симметричном расположении колеса и твердости HB<350 принимаем KHb=1,05; ≤[σH]. (23)
≤[σH]. (23) =366 (МПа) ≤ 410 (МПа)
=366 (МПа) ≤ 410 (МПа) ; (24)
; (24) ; (25)
; (25) =2158 (H)
=2158 (H) =900(H)
=900(H) ≤ [σF] (27)
≤ [σF] (27) По таблице 3.7 при ybd=1,45, симметричном расположении колес и твердости HB<350- KFb=1,13.
По таблице 3.7 при ybd=1,45, симметричном расположении колес и твердости HB<350- KFb=1,13.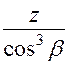 . (29)
. (29) = 37
= 37 = 134
= 134 (30)
(30)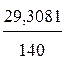 =0,79
=0,79 , (31)
, (31) =0,92
=0,92 . (32)
. (32) s°Flimb1=1,8∙230=415 (МПа)
s°Flimb1=1,8∙230=415 (МПа) =237 (МПа)
=237 (МПа) =206 (МПа)
=206 (МПа) = 61,6 (МПа)
= 61,6 (МПа) = 57,2 (МПа)
= 57,2 (МПа) 



