40. Вектор  утворює з координатними осями
утворює з координатними осями 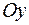 і
і  кути
кути  ,
,  . Обчислити координати вектора
. Обчислити координати вектора  при умові, що
при умові, що  .
.
41. Перевірити, чи являються дані точки  ,
,  ,
,  і
і  вершинами трапеції.
вершинами трапеції.
42. Дано вектор  . Знайти вектор
. Знайти вектор  , колінеарний вектору
, колінеарний вектору  і протилежного з ним напрямку, якщо
і протилежного з ним напрямку, якщо  .
.
43. Вектори 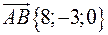 і
і  утворені відповідними сторонами трикутника
утворені відповідними сторонами трикутника  . Знайти вектори
. Знайти вектори  ,
,  і
і  , де
, де 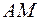 ,
,  і
і 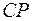 – медіани трикутника
– медіани трикутника  .
.
44. Обчислити вектор, колінеарний бісектрисі кута  трикутника
трикутника  , якщо вектори
, якщо вектори  і
і 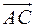 мають координати:
мають координати: 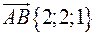 і
і  .
.
45. Вектор  утворює з координатними осями
утворює з координатними осями  і
і 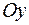 кути
кути  ,
,  . Обчислити його координати при умові, що
. Обчислити його координати при умові, що  .
.
46. Дано три вектора  ,
,  ,
,  . Знайти розклад вектора
. Знайти розклад вектора  по базису
по базису  ,
,  ,
,  .
.
47. Два вектори  ,
,  прикладені до однієї точки. Визначити координати вектора
прикладені до однієї точки. Визначити координати вектора  , напрямленого по бісектрисі кута між векторами
, напрямленого по бісектрисі кута між векторами  ,
,  , при умові, що
, при умові, що  .
.
48. Визначити при яких значеннях  і
і  вектори
вектори  і
і  колінеарні.
колінеарні.
49. Дано одну з вершин трикутника  і два вектори, які співпадають з двома його сторонами:
і два вектори, які співпадають з двома його сторонами:  і
і  . Знайти інші вершини трикутника і вектор
. Знайти інші вершини трикутника і вектор  .
.
50. Вектор  , колінеарний вектору
, колінеарний вектору  , утворює з віссю
, утворює з віссю 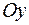 гострий кут. Знайти координати вектора
гострий кут. Знайти координати вектора  , якщо
, якщо  .
.
51. Знайти одиничний вектор, колінеарний вектору, напрямленому по бісектрисі кута  трикутника
трикутника  , якщо задано його вершини:
, якщо задано його вершини:  ,
,  ,
,  .
.
52. Вектор  , колінеарний вектору
, колінеарний вектору  , утворює з віссю
, утворює з віссю  гострий кут. Знаючи, що
гострий кут. Знаючи, що  , знайти його координати.
, знайти його координати.
53. Вектор утворює з осями  і
і  кути
кути  і
і  . Який кут він утворює з віссю
. Який кут він утворює з віссю 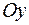 .
.
54. Визначити координати точки  , якщо її радіус-вектор утворює з координатними осями однакові кути і його модуль дорівнює
, якщо її радіус-вектор утворює з координатними осями однакові кути і його модуль дорівнює 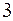 .
.
55. У площині  знайти вектор
знайти вектор 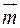 , перпендикулярний до вектора
, перпендикулярний до вектора  , що має однакову з ним довжину.
, що має однакову з ним довжину.
56. Дано три вектори  ,
,  і
і  . Знайти вектор
. Знайти вектор  , який одночасно задовольняє трьом рівнянням:
, який одночасно задовольняє трьом рівнянням:  ,
,  ,
,  .
.
57. Дано два вектори  і
і  . Знайти вектор
. Знайти вектор  , якщо він перпендикулярний до осі
, якщо він перпендикулярний до осі  і задовольняє умовам:
і задовольняє умовам:  ,
,  .
.
58. Три сили  ,
,  і
і  прикладені до однієї точки. Яку роботу виконує їх рівнодіюча, якщо точка їх прикладення, рухаючись прямолінійно, переміщується із
прикладені до однієї точки. Яку роботу виконує їх рівнодіюча, якщо точка їх прикладення, рухаючись прямолінійно, переміщується із  в
в 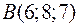 .
.
59. Дано три вектори: 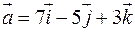 ,
,  і
і  . Знайти проекцію вектора
. Знайти проекцію вектора  на вектор
на вектор  .
.
60. Знайти вектор  , колінеарний вектору
, колінеарний вектору  , який задовольняє умові:
, який задовольняє умові:  .
.
61. Дано вершини чотирикутника  ,
,  ,
,  і
і  . Довести, що його діагоналі взаємно перпендикулярні.
. Довести, що його діагоналі взаємно перпендикулярні.
62. В просторі дано три не компланарні вектори  ,
,  і
і  . Знайти координати вектора
. Знайти координати вектора  , де
, де  – основа перпендикуляра, опущеного з точки
– основа перпендикуляра, опущеного з точки 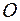 на площину
на площину  .
.
63. Дано трикутник  і відомі координати векторів
і відомі координати векторів  і
і  . Обчислити кути трикутника.
. Обчислити кути трикутника.
64. В трикутнику  , розташованому у просторі, відомі координати векторів
, розташованому у просторі, відомі координати векторів  і
і  . Визначити координати і довжину вектора
. Визначити координати і довжину вектора  , де
, де  – основа перпендикуляра, опущеного з вершини
– основа перпендикуляра, опущеного з вершини 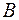 на протилежну сторону.
на протилежну сторону.
65. Дано трикутник з вершинами  ,
,  ,
,  . Обчислити його зовнішній кут при вершині
. Обчислити його зовнішній кут при вершині  .
.
66. Вектор  , колінеарний вектору
, колінеарний вектору  утворює гострий кут з віссю
утворює гострий кут з віссю  . Знаючи, що
. Знаючи, що  , знайти його координати.
, знайти його координати.
67. Вектор  , перпендикулярний до векторів
, перпендикулярний до векторів  і
і 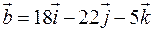 , утворює з віссю
, утворює з віссю 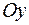 тупий кут. Знайти координати цього вектора, якщо
тупий кут. Знайти координати цього вектора, якщо  .
.
68. Знайти вектор  , знаючи, що він перпендикулярний до векторів
, знаючи, що він перпендикулярний до векторів  і
і  , і задовольняє умові
, і задовольняє умові  .
.
69. Обчислити довжину  діагоналі паралелепіпеда, знаючи довжини
діагоналі паралелепіпеда, знаючи довжини  ,
,  ,
, 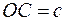 трьох його ребер і кути
трьох його ребер і кути  і
і  між ними.
між ними.
70. Якій умові повинні задовольняти вектори  і
і  , щоб вектори
, щоб вектори  і
і  були колінеарні.
були колінеарні.
71. Дано модулі векторів  і
і  ,
, 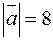 ,
,  , і їх скалярний добуток
, і їх скалярний добуток  . Обчислити модуль їх векторного добутку.
. Обчислити модуль їх векторного добутку.
72. Обчислити площу паралелограма, побудованого на векторах  і
і  , якщо
, якщо  ,
,  і
і  .
.
73. Знаючи сторони трикутника  і
і  . Обчислити довжину висоти
. Обчислити довжину висоти  .
.
74. Обчислити об’єм паралелепіпеда, побудованого на векторах 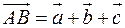 ,
,  і
і  .
.
75. Довести, що чотири точки  ,
, 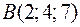 ,
, 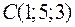 і
і  лежать в одній площині.
лежать в одній площині.
76. Обчислити відстань від точки  до прямої, яка проходить через точки
до прямої, яка проходить через точки  і
і  .
.
77. Обчислити синус кута між діагоналями паралелограма, який побудовано на даних векторах  і
і  , де
, де 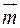 ,
,  ,
,  – взаємно перпендикулярні орти.
– взаємно перпендикулярні орти.
78. Обчислити проекцію вектора  на вісь, напрям якої визначається вектором
на вісь, напрям якої визначається вектором  , якщо
, якщо  ,
,  ,
,  – взаємно перпендикулярні орти.
– взаємно перпендикулярні орти.
79. Обчислити величину кута, утвореного векторами  і
і  .
.
80. Вектор  , перпендикулярний до векторів
, перпендикулярний до векторів  і
і  , утворює з віссю
, утворює з віссю 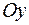 тупий кут. Знаючи, що
тупий кут. Знаючи, що  , знайти його координати.
, знайти його координати.
81. Об’єм тетраедра дорівнює  куб. одиниць, три його вершини знаходяться в точках
куб. одиниць, три його вершини знаходяться в точках  ,
,  і
і  . Знайти координати четвертої вершини
. Знайти координати четвертої вершини  , якщо відомо, що вона належить осі
, якщо відомо, що вона належить осі 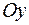 .
.
82. Вектор 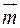 перпендикулярний до осі
перпендикулярний до осі  і до вектора
і до вектора 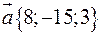 , утворює гострий кут з віссю
, утворює гострий кут з віссю  . Знаючи, що
. Знаючи, що  , знайти його координати.
, знайти його координати.
83. Знайти вектор  , якщо він перпендикулярний до векторів
, якщо він перпендикулярний до векторів  і
і  , і задовольняє умові
, і задовольняє умові  .
.
84. Об’єм трикутної піраміди  дорівнює
дорівнює 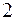 куб. Одиниці, а три її вершини знаходяться у точках
куб. Одиниці, а три її вершини знаходяться у точках  ,
,  і
і  . Знайти координати четвертої вершини
. Знайти координати четвертої вершини  , якщо відомо, що вона належить осі
, якщо відомо, що вона належить осі  .
.
85. Задані чотири вектори  ,
,  ,
,  ,
,  . Довести, що вектори
. Довести, що вектори  ,
,  ,
,  утворюють базис, та знайти координати вектора
утворюють базис, та знайти координати вектора  , в цьому базисі та,
, в цьому базисі та, 
a.  ,
,  ,
, 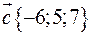 ,
, 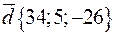 .
.
b.  ,
,  ,
,  ,
,  .
.
c.  ,
,  ,
,  ,
, 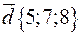 .
.
d.  ,
,  ,
,  ,
, 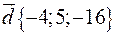 .
.
e.  ,
,  ,
,  ,
,  .
.
f.  ,
,  ,
,  ,
,  .
.
g.  ,
,  ,
,  ,
,  .
.
h.  ,
,  ,
,  ,
,  .
.
i.  ,
,  ,
,  ,
,  .
.
j. 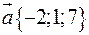 ,
,  ,
,  ,
,  .
.
Данные для заполнения отчета о прибылях и убытках за 2008г.
(руб.)
|
| За год
|
| Показатель
| отчетный
| прошлый
|
| Выручка (нетто) от продажи:
продукции собственного производства
товаров
|
5 075 600
2 550 067
|
3 728 000
2 561 000
|
| Фактическая себестоимость проданных:
продукции собственного производства
товаров
|
3 855 000
2 216 217
|
2 208 500
1 890 000
|
| Расходы, связанные с продажей продукции, товаров
|
| 152 600
|
| Общехозяйственные расходы
|
| 496 250
|
| Начисленные к получению проценты по займам
| 30 000
| —
|
| Начисленные к получению суммы за хранение денежных средств на расчетном счете
| 1 000
| —
|
| Начисленные к уплате проценты по кредитам
| 254 960
| 100 000
|
| Оприходованы материалы, полученные в результате ликвидации ОС; излишки, выявленные в ходе инвентаризации
| 169 760
|
|
| Штрафы, пени, начисленные к получению
| 50 000
| 10 000
|
| Налог на имущество
| 56 250
| 45 613
|
| Убыток от списания морально устаревшего оборудования
| 15 000
| —
|
| Суммы дебиторской задолженности, по которой истек срок исковой давности
| 27 560
| —
|
| Убытки от хищений, виновники которых не найдены
| 23 450
| —
|
| Начислен условный расход (доход) по налогу на прибыль
| ?
| ?
|
| Текущий налог на прибыль
| ?
| ?
|
| Постоянные налоговые обязательства
| (18 115)
| (5 000)
|
| Согласно протоколу собрания учредителей за счет нераспределенной прибыли прошлых лет:
Произведены отчисления в резервный капитал
начислены дивиденды
|
50 000
200 000
| |
| Выплачены дивиденды учредителям
Удержан и перечислен в бюджет налог на доходы (9%)
|
| -
|
| Произведено увеличение уставного капитала за счет внесения дополнительных вкладов участниками
| 500 000
| -
|
| Внесены на расчетный счет дополнительные вклады учредителей
|
| -
|
Общество с ограниченной ответственностью «Спектр» занимается производством одного вида промышленной продукции. Кроме того, организация осуществляет торговую деятельность, связанную с покупкой и продажей товаров. Вспомогательного производства нет.
Реквизиты ООО «Спектр»:
ИНН 7209047520
ОКПО 05831119
ОКВЭД 66000
ОКФС16
Почтовый адрес: 625000, г. Тюмень, ул. Машиностроителей, 18.
Отчетность составляется в тысячах рублей.

 утворює з координатними осями
утворює з координатними осями 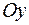 і
і  кути
кути  ,
,  . Обчислити координати вектора
. Обчислити координати вектора  .
. ,
,  ,
,  і
і  вершинами трапеції.
вершинами трапеції. . Знайти вектор
. Знайти вектор  , колінеарний вектору
, колінеарний вектору  і протилежного з ним напрямку, якщо
і протилежного з ним напрямку, якщо  .
.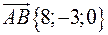 і
і  утворені відповідними сторонами трикутника
утворені відповідними сторонами трикутника  . Знайти вектори
. Знайти вектори  ,
,  і
і  , де
, де 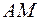 ,
,  і
і 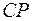 – медіани трикутника
– медіани трикутника  трикутника
трикутника  і
і 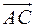 мають координати:
мають координати: 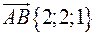 і
і  .
. і
і  ,
,  .
. ,
,  ,
,  . Знайти розклад вектора
. Знайти розклад вектора  по базису
по базису  ,
,  ,
,  .
. ,
,  прикладені до однієї точки. Визначити координати вектора
прикладені до однієї точки. Визначити координати вектора  , при умові, що
, при умові, що  .
. і
і  вектори
вектори  і
і  колінеарні.
колінеарні. і два вектори, які співпадають з двома його сторонами:
і два вектори, які співпадають з двома його сторонами:  і
і  . Знайти інші вершини трикутника і вектор
. Знайти інші вершини трикутника і вектор  .
. , утворює з віссю
, утворює з віссю  .
. трикутника
трикутника  ,
,  ,
,  .
. , утворює з віссю
, утворює з віссю  , знайти його координати.
, знайти його координати. і
і  , якщо її радіус-вектор утворює з координатними осями однакові кути і його модуль дорівнює
, якщо її радіус-вектор утворює з координатними осями однакові кути і його модуль дорівнює 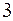 .
. знайти вектор
знайти вектор 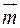 , перпендикулярний до вектора
, перпендикулярний до вектора  , що має однакову з ним довжину.
, що має однакову з ним довжину. ,
,  і
і  . Знайти вектор
. Знайти вектор  , який одночасно задовольняє трьом рівнянням:
, який одночасно задовольняє трьом рівнянням:  ,
,  ,
,  .
. і
і  . Знайти вектор
. Знайти вектор  ,
,  .
. ,
,  і
і  прикладені до однієї точки. Яку роботу виконує їх рівнодіюча, якщо точка їх прикладення, рухаючись прямолінійно, переміщується із
прикладені до однієї точки. Яку роботу виконує їх рівнодіюча, якщо точка їх прикладення, рухаючись прямолінійно, переміщується із  в
в 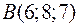 .
.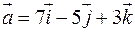 ,
,  і
і  . Знайти проекцію вектора
. Знайти проекцію вектора  на вектор
на вектор  , який задовольняє умові:
, який задовольняє умові:  .
. ,
,  ,
,  і
і  . Довести, що його діагоналі взаємно перпендикулярні.
. Довести, що його діагоналі взаємно перпендикулярні. ,
,  і
і  . Знайти координати вектора
. Знайти координати вектора  , де
, де  – основа перпендикуляра, опущеного з точки
– основа перпендикуляра, опущеного з точки 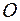 на площину
на площину  і відомі координати векторів
і відомі координати векторів  і
і  . Обчислити кути трикутника.
. Обчислити кути трикутника. і
і  . Визначити координати і довжину вектора
. Визначити координати і довжину вектора  , де
, де 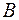 на протилежну сторону.
на протилежну сторону. ,
,  ,
,  . Обчислити його зовнішній кут при вершині
. Обчислити його зовнішній кут при вершині  .
. утворює гострий кут з віссю
утворює гострий кут з віссю  , знайти його координати.
, знайти його координати. і
і 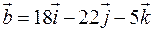 , утворює з віссю
, утворює з віссю  .
. і
і  , і задовольняє умові
, і задовольняє умові  .
. діагоналі паралелепіпеда, знаючи довжини
діагоналі паралелепіпеда, знаючи довжини  ,
,  ,
, 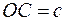 трьох його ребер і кути
трьох його ребер і кути  і
і  між ними.
між ними. і
і  були колінеарні.
були колінеарні.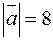 ,
,  , і їх скалярний добуток
, і їх скалярний добуток  . Обчислити модуль їх векторного добутку.
. Обчислити модуль їх векторного добутку. і
і  , якщо
, якщо  ,
,  і
і  .
. і
і  . Обчислити довжину висоти
. Обчислити довжину висоти  .
.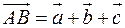 ,
,  і
і  .
. ,
, 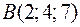 ,
, 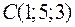 і
і  лежать в одній площині.
лежать в одній площині. до прямої, яка проходить через точки
до прямої, яка проходить через точки  і
і  .
. і
і  , де
, де  ,
,  на вісь, напрям якої визначається вектором
на вісь, напрям якої визначається вектором  , якщо
, якщо  і
і  .
. і
і  , утворює з віссю
, утворює з віссю  , знайти його координати.
, знайти його координати. куб. одиниць, три його вершини знаходяться в точках
куб. одиниць, три його вершини знаходяться в точках  ,
,  . Знайти координати четвертої вершини
. Знайти координати четвертої вершини  , якщо відомо, що вона належить осі
, якщо відомо, що вона належить осі 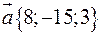 , утворює гострий кут з віссю
, утворює гострий кут з віссю  , знайти його координати.
, знайти його координати. і
і  .
. дорівнює
дорівнює 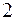 куб. Одиниці, а три її вершини знаходяться у точках
куб. Одиниці, а три її вершини знаходяться у точках  ,
,  і
і  . Знайти координати четвертої вершини
. Знайти координати четвертої вершини 
 ,
,  ,
, 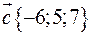 ,
, 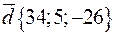 .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
, 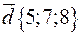 .
. ,
,  ,
,  ,
, 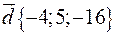 .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
.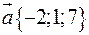 ,
,  ,
,  ,
,  .
.


