ИНФОРМАЦИОННОЕ СООБЩЕНИЕ
1. Для больших скоростей машины сила сопротивления пропорциональна квадрату скорости с коэффициентом, который определяется геометрией машины. Поскольку речь идет о машинах одного класса, имеющих близкие размеры, можно ожидать, что для всех машин коэффициенты пропорциональности близки. Поэтому
Радиус изгиба можно найти из следующих соображений. Пусть биметаллическая пластина нагрелась на
где
Отсюда, пренебрегая произведением двух малых величин, находим
Величину прогиба пластины (величина
Если угол
(это равенство можно получить из основного тригонометрического тождества и первого замечательного предела
Подставляя в эту формулу данные в условии числа, найдем
Величина удлинения пластины составит
Сначала рассмотрим шарнир А. Поскольку Стержень АС сжат, а АВ растянут, на шарнир А действуют такие силы – сила натяжения нити, равная силе тяжести груза и силы натяжения стержней АВ и АС. Чтобы шарнир был в равновесии, сумма этих сил должна быть равна нулю. А поскольку углы между этими силами равны Рассмотрим теперь шарнир В. На него действуют три силы, сумма которых равна нулю, которые направлены под углами
(1) при Если
(2) при
Если
(3) Графики зависимости напряжения и тока через стабилитрон и бареттер, а также тока через резистор от ЭДС источника ((1)-(3)) приведены на рисунке 1.
Рассмотрим сначала случай, когда падающий луч параллелен одной из плоскостей отражателя. Тогда этот луч будет отражаться только от двух его граней, и отраженный луч будет лежать в плоскости, перпендикулярной этим граням (в этом случае задача, фактически, является плоской). Строя ход луча по правилам отражения (угол падения равен углу отражения), убеждаемся, что отраженный луч будет распространяться в направлении, обратном падающему (см. рисунок; параллельность падающего и отраженного лучей следует, например, из равенства углов, отмеченных на рисунке дугами). Для доказательства сделанного выше утверждения в общем случае заметим, что для проекции падающего и отраженного луча на любую плоскость также будет справедливо утверждение – угол падения равен углу отражения. Поэтому падающий и отраженные лучи можно спроецировать на плоскости, параллельные граням отражателя, для проекций справедливо сделанное выше построение, откуда и следует сделанное утверждение. На Луноходе блок уголковых отражателей размещался с целью точного определения расстояния от Земли до Луны. Лазерный луч (имеющий малую расходимость) направлялся на отражатель и в той же точке на Земле регистрировался отраженный луч. По времени задержки можно было определить расстояние от точки, из которой направлялся луч, до Лунохода с высокой точностью и сравнить его со значениями расстояния до Луны, полученными другими методами. Была и еще одна цель размещения отражателей на Луноходе - политическая. После американских экспедиций на Луну возник и активно муссировался в прессе слух, что на Луне американские астронавты якобы не были, а показанные по телевидению кадры высадки на Луну сняты на Земле. Так вот размещение уголкового отражателя на Луноходе позволяло любому человеку на Земле (обладающему минимальным набором лабораторного оборудования) проверить факт нахождения отражателя на Луне. По данным Центра управления полетами за время работы Лунохода на Луне было зарегистрировано более 50 попыток посылки лазерного луча на отражатель (кроме тех, что были сделаны для лазерного зондирования Луны советскими астрономами). 6. Решение. Работа пороховых газов идет на разгон пули. Поэтому
где
Используем:
ИНФОРМАЦИОННОЕ СООБЩЕНИЕ Уважаемые коллеги!
Правительство Пермского края Министерство промышленности, инноваций и науки Пермского края Пермский филиал ФГБУН Института экономики Уральского отделения РАН НОУ ВПО «Западно-Уральский институт экономики и права», г. Пермь Кафедра предпринимательства и управления
приглашают принять участие
|

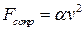 , а мощность есть
, а мощность есть 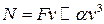 .
.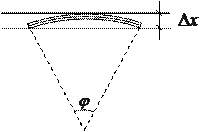 2. Из-за разных коэффициентов теплового расширения пластины двух металлов по-разному удлиняются при нагревании (или сжимаются при охлаждении). А поскольку они спаяны по всей площади контакта, пластине выгоднее согнуться, чем растягивать один и сжимать другой металл. Причем при нагревании внутри изгиба будет пластинка из того металла, который меньше расширяется при нагревании.
2. Из-за разных коэффициентов теплового расширения пластины двух металлов по-разному удлиняются при нагревании (или сжимаются при охлаждении). А поскольку они спаяны по всей площади контакта, пластине выгоднее согнуться, чем растягивать один и сжимать другой металл. Причем при нагревании внутри изгиба будет пластинка из того металла, который меньше расширяется при нагревании. . Тогда пластинки, из которых она состоит, удлинятся на следующие величины
. Тогда пластинки, из которых она состоит, удлинятся на следующие величины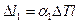 и
и 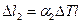
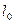 - первоначальная длина пластинок. Следовательно, для угла на который опирается пластина после изгиба, можно записать (с учетом малой толщины пластины)
- первоначальная длина пластинок. Следовательно, для угла на который опирается пластина после изгиба, можно записать (с учетом малой толщины пластины)
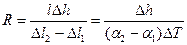
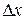 на рисунке) можно найти как
на рисунке) можно найти как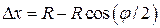 (*)
(*)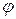 много меньше 1 радиана (для реальных пластин это условие выполнено), то
много меньше 1 радиана (для реальных пластин это условие выполнено), то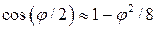
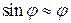 ), то формулу (*) можно привести к виду
), то формулу (*) можно привести к виду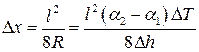
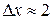 мм
мм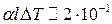 мм, т.е. на порядок меньше.
мм, т.е. на порядок меньше. 3. Если удалить стержень ВС, то, очевидно, точки В и С начнут сближаться, поскольку треугольник CDE останется на месте, а ромб CABD будет «складываться». Поэтому стержень ВС сжат. Аналогично заключаем, что стержень АВ растянут, АС – сжат.
3. Если удалить стержень ВС, то, очевидно, точки В и С начнут сближаться, поскольку треугольник CDE останется на месте, а ромб CABD будет «складываться». Поэтому стержень ВС сжат. Аналогично заключаем, что стержень АВ растянут, АС – сжат.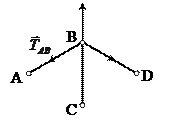 Найдем силу натяжения стержня ВС. Во-первых, заметим, что воздействие шарнира на стержня или стержня на шарнир может осуществляться только вдоль стержня (в противном случае условие равновесия стержня не будет выполняться).
Найдем силу натяжения стержня ВС. Во-первых, заметим, что воздействие шарнира на стержня или стержня на шарнир может осуществляться только вдоль стержня (в противном случае условие равновесия стержня не будет выполняться).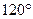 , то их сумма равна нулю только в том случае, когда равны их величины. Поэтому
, то их сумма равна нулю только в том случае, когда равны их величины. Поэтому 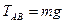 ,
, 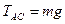 .
.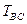 и
и  равны друг другу и силе
равны друг другу и силе 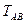 . Потому
. Потому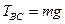
 4. Решение. Рассмотрим сначала случай малых значений ЭДС источника. Если
4. Решение. Рассмотрим сначала случай малых значений ЭДС источника. Если  , ток в цепи не может быть больше, чем
, ток в цепи не может быть больше, чем 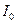 , и, следовательно, напряжение на бареттере (и стабилитроне) равно нулю. Поэтому ток через стабилитрон равен нулю, ток через бареттер равен току через резистор:
, и, следовательно, напряжение на бареттере (и стабилитроне) равно нулю. Поэтому ток через стабилитрон равен нулю, ток через бареттер равен току через резистор: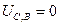 ,
, 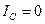 ,
, 
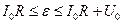 , ток через резистор превосходит
, ток через резистор превосходит 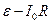 , т.е. меньше, чем
, т.е. меньше, чем 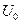 , поэтому ток через стабилитрон будет равен нулю:
, поэтому ток через стабилитрон будет равен нулю: ,
, 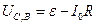
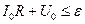 , ток через бареттер равен
, ток через бареттер равен 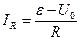 , ток через стабилитрон равен разности тока через резистор и тока через бареттер:
, ток через стабилитрон равен разности тока через резистор и тока через бареттер: ,
, 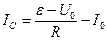 ,
, 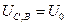
 5. Решение. Докажем, что как бы ни падал луч на отражатель, после отражения он будет распространяться точно в обратном направлении.
5. Решение. Докажем, что как бы ни падал луч на отражатель, после отражения он будет распространяться точно в обратном направлении.
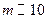 г – масса пули,
г – масса пули,  см2 – площадь сечения ствола ружья,
см2 – площадь сечения ствола ружья, 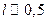 м – длина ствола,
м – длина ствола, 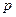 - среднее давление, 0,5 - доля работы, идущая на разгон пули. Отсюда получаем
- среднее давление, 0,5 - доля работы, идущая на разгон пули. Отсюда получаем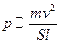
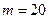 г,
г,  м/с,
м/с, 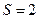 см2,
см2, 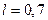 м. Отсюда
м. Отсюда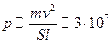 Па
Па  атм
атм


