Разработчик доц., к.т.н. Ермолаев
Рецензент проф., д.т.н. Подгорный Ю.И.
Работа выполнена на кафедре механики НТИ МГУДТ (филиал)
1 ОБЩИЕ МЕТОДЫ ПОСТРОЕНИЯ АЛГОРИТМОВ И ПРОГРАММ Любой механизм второго класса образуется присоединением к ведущему звену или механизму первого класса кинематической цепи, состоящей из двухповодковых групп разных видов [1]. Таким образом, задачи кинематического и силового расчета многозвенных механизмов аналитическими методами можно свести к задачам кинематического и силового анализа разновидностей структурных групп второго класса. При составлении алгоритмов кинематического и силового анализа механизмов второго класса применяются общие методы определения координат точек звеньев, положений звеньев, их скоростей и ускорений, определение сил инерции, реакций в кинематических парах, приведение сил к равнодействующей, независимо от вида структурных групп, входящих в состав механизма. Для определения или задания движения точки звена применяется координатный способ [2]. В соответствии с рисунком 1 положение точки А в заданной системе координат ХОY определяется координатами Положение звена на координатной плоскости ХОY (рисунок 1) может быть задано двумя способами: координатами двух точек
б)
Во втором случае находятся координаты точки В:
Положение произвольной точки С на звене АВ задается в системе подвижных координат
Проекции векторов скоростей и ускорений точек В или С определяются дифференцированием уравнений (5) или (6). Аналогично определяются положения, проекции векторов скоростей и ускорений любых точек на звеньях структурных групп. Для многократного повторения алгоритма анализа двухповодковой группы в программах анализа и синтеза механизмов его целесообразно оформить в виде подпрограммы. Подпрограмма является самостоятельной программной единицей практически для всех известных алгоритмических языков и систем. Подпрограмма описывается определенным служебным словом – оператором подпрограммы. В дальнейшем подпрограмму будем описывать оператором подпрограммы – ПОДПРОГРАММА. Описание подпрограммы состоит из имени и тела. Имя подпрограммы включает в себя идентификатор подпрограммы и список формальных параметров. Тело подпрограммы представляет оператор (составной или блок), описывающий алгоритм стандартной части вычислений с использованием формальных параметров и локальных величин, описанных в теле подпрограммы. Идентификатор подпрограммы удобно обозначать первыми буквами слов, соответствующих назначению алгоритма, вида звена или номера группы. Например, КАВЗ – кинематический анализ ведущего звена (для алгоритмических языков, не допускающих применение букв русского алфавита, идентификатор подпрограммы набирается буквами латинского алфавита, например, KAWZ); КАГ1 – кинематический анализ группы с тремя вращательными кинематическими парами; КАГ2 – кинематический анализ группы с внешней поступательной; КАГ3 - кинематический анализ группы с внутренней поступательной парой и т.п.
2 МЕТОДИКА СОСТАВЛЕНИЯ АЛГОРИТМА И ПРОГРАММЫ КИНЕМАТИЧЕСКОГО АНАЛИЗА ВРАЩАЮЩЕГОСЯ ВЕДУЩЕГО ЗВЕНА При кинематическом анализе вращающего ведущего звена должны быть заданы следующие параметры в соответствии с рисунком 2:
В результате расчета определяются: координаты, проекции векторов скорости и ускорения точки А присоединения структурной группы Ассура - Вычисление кинематических характеристик ведущего звена осуществляется по алгоритму 1. В формулах алгоритма 1 знаки координат, проекций векторов скорости и ускорения точки А определяются знаками тригонометрических функций угла Алгоритм 1 оформлен в виде подпрограммы с именем КАВЗ и составлена инструкция по ее применению.
Алгоритм 1 - Кинематический анализ вращающегося ведущего звена 1. 2. 3. 4. 5. 6.
Рисунок 2 – Расчетная схема вращающегося ведущего звена.
|

 , а ее скорость и ускорение – проекциями на соответствующие координатные оси:
, а ее скорость и ускорение – проекциями на соответствующие координатные оси: 
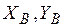 этого звена либо координатами одной точки, например А, и углом a между осью звена и осью абсцисс. В первом случае при кинематическом анализе необходимо найти угол a и его ориентацию на координатной плоскости при отсчете угла в положительном направлении. Этот угол находится как угол наклона прямой, проходящей через две точки:
этого звена либо координатами одной точки, например А, и углом a между осью звена и осью абсцисс. В первом случае при кинематическом анализе необходимо найти угол a и его ориентацию на координатной плоскости при отсчете угла в положительном направлении. Этот угол находится как угол наклона прямой, проходящей через две точки: (1)
(1)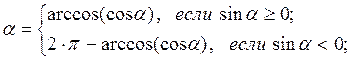 (2)
(2)


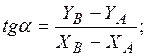 (3)
(3) (4)
(4) (5)
(5)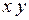 (рисунок 1б), тогда ее координаты в заданной системе координат ХОY определятся из следующих уравнений:
(рисунок 1б), тогда ее координаты в заданной системе координат ХОY определятся из следующих уравнений: (6)
(6) - длина звена
- длина звена  ;
; - координаты кинематической пары
- координаты кинематической пары  в заданной системе координат XOY;
в заданной системе координат XOY; - угловая координата, угловая скорость и угловое ускорение звена
- угловая координата, угловая скорость и угловое ускорение звена 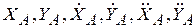 .
. , направлениями угловой скорости
, направлениями угловой скорости  и углового ускорения
и углового ускорения  . Направление угла
. Направление угла  ;
; ;
; ;
; ;
;
 ;
; .
.


