Диффузия из источника ограниченной мощности
Профиль распределения примеси описывается уравнением Гаусса:
Начальные условия: N(x, 0)=0. Граничные условия: Q0 - число атомов легирующего вещества, осажденного на единицу площади полупроводника, равно интегралу от N(x, t) по всей глубине полупроводника и N(x, t>>0)=0. При x=0 концентрация легирующей примеси на поверхности будет равна:
Количество диффузанта, необходимого для осуществления диффузии на определенную глубину полупроводника заданного количества примеси, изменяющейся пропорционально exp(-z2), где z = 0.5x
где Q0 - количество примеси, поступающее в течение преддиффузии, N01 - поверхностная концентрация при температуре преддиффузии, D1 - коэффициент диффузии при температуре преддиффузии, t1 - продолжительность преддиффузии. Общее уравнение, позволяющее определить концентрацию примеси в полупроводнике, записывается в следующем виде:
где индексы 1 относятся к разгонке примеси из источника сформированного на преддиффузии, а индексы 2 - к самому процессу диффузии. Уравнение (7.9) справедливо для случая, когда выполняется следующее условие:
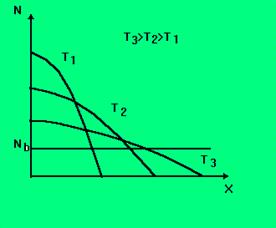
На рис. 7.7 изображен профиль легирования из ограниченного источника.
Рис. 7.7. Рис. 7.8
Профили легирования при диффузии из бесконечного (кривая 1) и ограниченного (кривая 2) источников в сравнении изображены на рис. 7.8.
Рис. 7.9. Формирование областей базы и эммитера биполярного транзистора
На рис. 7.9 показано формирование областей базы и эммитера биполярного транзистора и указаны возможные значения глубин слоев с разным типом проводимости.
|

 (7.6)
(7.6) (7.7)
(7.7) , очень мало. Такое количество примеси можно ввести ионным легированием или предварительным проведением диффузии (преддиффузии) при низкой температуре в течение короткого времени. При этом на поверхности сформируется источник с необходимым малым содержанием примеси Q0:
, очень мало. Такое количество примеси можно ввести ионным легированием или предварительным проведением диффузии (преддиффузии) при низкой температуре в течение короткого времени. При этом на поверхности сформируется источник с необходимым малым содержанием примеси Q0: , (7.8)
, (7.8)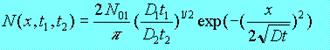 , (7.9)
, (7.9)