Теоретическая часть. В результате приходим к нелинейному дифференциальному уравнению
…… В результате приходим к нелинейному дифференциальному уравнению
….. Составим расширенную характеристическую систему с дополнительным аргументом
Получим систему интегральных уравнений
Запишем последовательные приближения
Оценивая правые части последовательных приближений, приходим к выводу, что при
где
выполняются неравенства
Рассмотрим вектор
Тогда получаем:
где
Получим, что ряды Единственность следует из того факта, что для разности двух возможных решений будет выполняться неравенство вида
где Далее докажем существование, непрерывность и ограниченность частных производных функций
Снова введем в рассмотрение вектор
Тогда получаем:
где
Показывается, что последовательность Для доказательства сходимости рассмотрим линейные интегральные уравнения относительно неизвестных функций Реализация: В процессе прохождения научно-исследовательской практики на кафедре «Прикладная математика» определила условия локальной разрешимости нового вида нелинейного дифференциального уравнения: были построены последовательные приближения, доказана их ограниченность и сходимость. Так же с помощью последовательных приближений была доказана ограниченность и сходимость производных первого порядка. Для частного случая лиминального уравнения проводится численная реализация, которая на данный момент находится в стадии разработки. Результат работы: Задание, поставленное на практику, было реализовано студенткой Хитевой Дарьей Вячеславовной в полном объеме. В дальнейшем планируется продолжить исследования лиминального уравнения, его нелокальной разрешимости.
Список использованной литературы (сам заголовок должен быть по центру, а перечисление «выравнивание по левому краю») (не менее 10 ссылок)
|

 ,
,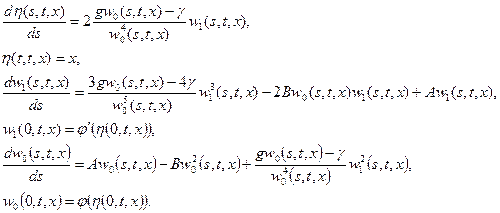

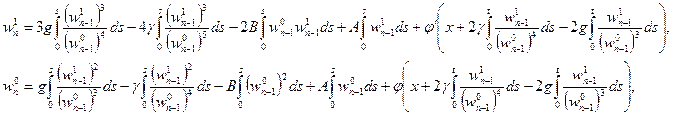
 ,
, ,
, ,
, .
. . Доказывается, что последовательные приближения
. Доказывается, что последовательные приближения  сходятся по норме к вектору
сходятся по норме к вектору  . За норму вектора
. За норму вектора 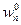 и
и 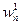 :
: .
. ,
,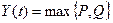 ,
, ,
,  ,
, ,
,  ,
,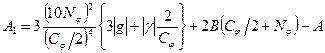 ,
,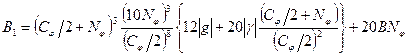 ,
, ,
, .
.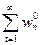 и
и  сходятся к функциям
сходятся к функциям  ,
,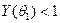 .
.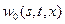 и
и  . Запишем последовательные приближения:
. Запишем последовательные приближения:

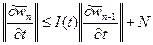 ,
,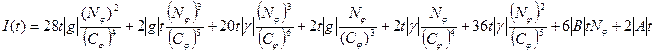 ,
,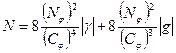 .
.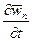 ограничена по норме. Следовательно, ограничены по норме и последовательности
ограничена по норме. Следовательно, ограничены по норме и последовательности  ,
,  .
.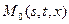 и
и  .
.


