ББК 32.973 8 страница

! Как называется проблема? Рыбная ловля.

! Из скольких частей состоит проблема? Из четырех.

! Как называется каждая часть? 1. Подготовка к ловле. 2. Ожидание клева. 3. Рыбацкая работа. 4. Обратная дорога.

Дополнительные удобства связаны с тем, что шапка занимает “парадное” место в поле чертежа, а названия смысловых частей помещаются внутри особых рамок уникальной формы и благодаря этому моментально приковывают к себе внимание читателя без всяких усилий с его стороны.

Таким образом, ДРАКОН предоставляет читателю эффективный трехэтапный метод познания незнакомой или забытой проблемы. На первом этапе, анализируя шапку, читатель узнает назначение алгоритма и его деление на смысловые части (ветки). На втором — осуществляется углубленный анализ каждой ветки. На третьем производится разбор взаимодействия веток.

ЧТО ЛУЧШЕ: ПРИМИТИВ ИЛИ СИЛУЭТ?

Дракон-схема с ветками называется силуэтом, без веток — примитивом. Силуэт, представленный на рис. 6 а, можно изобразить в виде примитива (рис. 6 б). Примитив есть последовательное соединение иконы “заголовок” шампур-блоков и иконы “конец”. У примитива иконы “заголовок” и “конец” обязательно лежат на одной вертикали, которая называется шампуром. На этой же линии лежат главные вертикали шампур-блоков. Образно говоря, шампур пронизывает иконы примитива (возможно, не все) подобно тому, как настоящий шампур пронизывает кусочки шашлыка.

Примитив рекомендуется использовать, если дракон-схема очень простая (примитивная) и содержит не более 5...15 икон. В противном случае, чтобы улучшить читаемость программы, выгоднее использовать силуэт. Нарушение этого правила обычно чревато неприятностями, ибо мешает читателю выявить сущность решаемой проблемы и, следовательно, затрудняет и замедляет понимание смысла программы.

Например, алгоритм на рис. 6 б выглядит громоздким и неоправданно сложным для восприятия. Это вызвано тем, что он содержит 19 икон, однако изображен в виде примитива. Криминал в том, что схема на рис. 6 б не позволяет читателю мгновенно (за несколько секунд) распознать визуально-смысловую структуру алгоритма. В самом деле, из скольких частей состоит решаемая проблема? Глядя на рис. 6 б, ответить на этот вопрос довольно трудно, а быстро ответить — невозможно. Положение в корне меняется, когда мы смотрим на рис. 6 а, где тот же самый алгоритм изображен в виде силуэта. Тут, как говорится, и ежу ясно: алгоритм состоит из четырех частей: “поиск автобуса”, “ожидание посадки”, “посадка в автобус”, “поездка”. Однако это не все: не менее важно и то обстоятельство, что запутанность зрительного рисунка исчезла и схема приобрела новое эстетическое (эргономическое) качество: элегантность, ясность и прозрачность.

Таким образом, в сложных случаях силуэт позволяет существенно уменьшить интеллектуальные усилия, затрачиваемые на понимание алгоритма. В силуэте крупные структурные части программы (ветки) четко выделены, они пространственно разнесены в поле чертежа, образуя вместе с тем легко узнаваемый, стабильный, предсказуемый и целостный зрительный образ. А в примитиве структурные части не выделены и перемешаны (“всё в одной куче”), что затрудняет чтение и анализ сложных алгоритмов. Однако для простых случаев (менее 5...15 икон) примитив, как правило, оказывается более предпочтительным.

КАК ОПИСАТЬ СИЛУЭТ С ПОМОЩЬЮ
ТЕКСТОВОГО ЯЗЫКА?

Из рис. 7 видно, что для описания веток в текстовый язык пришлось внести ряд изменений. В частности, появились два новых текстовых оператора, отсутствующие в традиционных языках:

ВЕТКА < идентификатор ветки >

АДРЕС < идентификатор ветки >

Оператор текстового языка ВЕТКА объявляет название ветки (записываемое на визуальном языке внутри иконы “имя ветки”). Оператор АДРЕС безусловно передает управление на текстовый оператор ВЕТКА, имя которой записано справа от оператора АДРЕС.

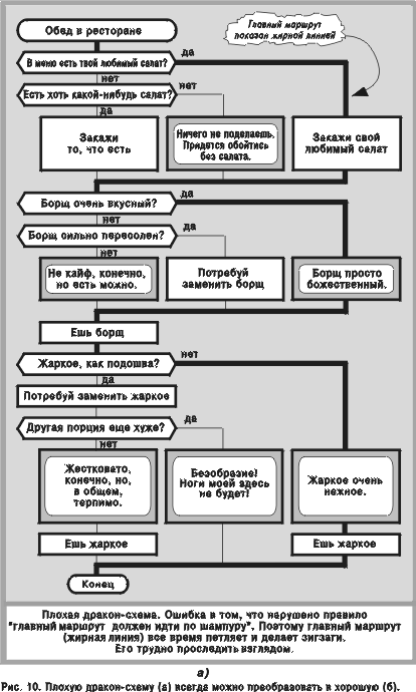
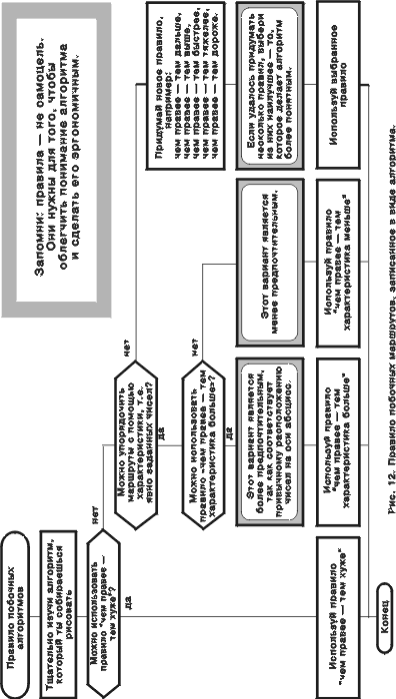
Сравнивая два языка: визуальный и текстовый, можно заметить, что соответствующие алгоритмы (рис. 6 а и 7) эквивалентны[14]. Однако визуальный язык несомненно более нагляден и доходчив. Второе преимущество состоит в том, что графика позволяет полностью исключить избыточные (паразитные) элементы, каковыми в текстовом языке оказываются почти все ключевые слова: АЛГОРИТМ, ВЕТКА, АДРЕС, КОНЕЦ ВЕТКИ, ЕСЛИ, ТО, ИНАЧЕ, КОНЕЦ ЕСЛИ, ЦИКЛ ЖДАТЬ, КОНЕЦ ЦИКЛА, КОММЕНТАРИЙ, ПЕРЕХОД НА, а также метки.

ЕСТЬ ЛИ В АЛГОРИТМЕ
“ЦАРСКАЯ ДОРОГА”?

Рассмотрим задачу. В запутанном лабиринте, соединяющем начало и конец сложного алгоритма, нужно выделить один-единственный маршрут — “путеводную нить”, с которой можно зрительно сравнивать все прочие маршруты, чтобы легко сориентироваться в проблеме и не заблудиться в путанице развилок. Эта путеводная нить (назовем ее “главный маршрут”) должна быть визуально легко различимой. Иными словами, бросив беглый взгляд на дракон-схему, мы должны обнаружить четкие ориентиры, благодаря которым можно сразу и безошибочно увидеть “царский” маршрут и упорядоченные относительно него остальные маршруты.

Для этого вводится правило: “главный маршрут примитива должен идти по шампуру”. Меняя местами слова “да” и “нет” в развилках и варианты в переключателях (а также присоединенные к ним гирлянды икон), следует добиться, чтобы на царском пути оказался тот выход развилки или переключателя, который ведет к наибольшему успеху (рис. 8). А побочные маршруты нужно расположить по правилу: “чем правее — тем хуже” (рис. 9). Если эти правила нарушены, дракон-схема считается плохой (рис. 10 а). Однако ее всегда можно превратить в хорошую (рис. 10 б).

В тех случаях, когда признак “лучше—хуже” не работает, вместо него следует выбрать какой-либо другой разумный критерий, чтобы смещение вправо от главного маршрута всегда было не произвольным и хаотичным, а продуманным и упорядоченным. Например, при решении математических задач выходы развилки и варианты переключателя можно расположить слева направо в порядке увеличения или уменьшения математической величины (характеристики), соответствующей этим выходам (рис. 11, 12).

ГЛАВНЫЙ МАРШРУТ СИЛУЭТА

В предыдущем параграфе мы узнали, как упорядочить маршруты примитива. Теперь настала очередь силуэта.

Шампуром ветки называется вертикаль, соединяющая икону “имя ветки” с иконой “адрес”, а если у ветки несколько выходов — с левым из них. Для ветки сохраняют силу оба “царских” правила:

! главный маршрут ветки должен идти по шампуру;

! побочные маршруты ветки следует упорядочить слева направо по какому-либо критерию.

Предположим, в качестве критерия выбран принцип “чем правее — тем хуже”. В этом случае каждая ветка силуэта должна быть построена по единому правилу: чем правее (чем дальше от шампура данной ветки) расположена очередная вертикаль, тем менее успешные действия она выполняет.

Например, на рис. 6 а ветка “посадка в автобус” имеет три вертикали. Левая вертикаль (главный маршрут) описывает наибольший успех, так как вы будете ехать в автобусе сидя. Правая вертикаль означает наименьший успех, поскольку вы вышли из автобуса и поездка отклады­вается. Средняя вертикаль (расположенная выше иконы “Есть желание ехать стоя?”) занимает промежуточное положение, потому что —
в зависимости от ответа — может иметь место либо частичный успех (вы будете ехать, но не сидя, а стоя), либо неудача, поскольку вы выходите из автобуса несолоно хлебавши.

Главный маршрут силуэта — последовательное соединение главных маршрутов поочередно работающих веток. Таким образом, ДРАКОН позволяет читателю моментально увидеть главный маршрут любого, сколь угодно сложного и разветвленного алгоритма и, сверх того, делает смещение всех побочных маршрутов относительно “царского” не случайным, а осмысленным и предсказуемым, т. е. легким для вос­приятия.

ПЕРЕСЕЧЕНИЯ ЛИНИЙ? — БОЖЕ УПАСИ!

Некоторые специалисты, склонные к резким выражениям, называют традиционные блок-схемы алгоритмов [2] “помоечными блок-схе­мами”, потому что изображенные на них хитросплетения блоков, соединенные хаосом куда угодно гуляющих рваных линий больше напоминают кучу мусора, нежели регулярную структуру. ДРАКОН выгодно отличается тем, что его графический узор имеет строгое матема­тическое и когнитивно-эргономическое обоснование и подчиняется жестким и тщательно продуманным правилам. Среди них особое место занимает правило: “пересечения и обрывы соединительных линий запрещены”.

Рис. 10. Плохую дракон-схему (а) всегда можно преобразовать в хорошую (б)

10а

Рис. 10 (окончание)

10б

Рис. 11. Маршруты упорядочены слева направо согласно правилу “чем правее — тем скорость больше”

11

12

При вычерчивании обычных блок-схем допускаются два типа пересечения линий: явное, изображенное крестом линий, и замаскированное, выполняемое с помощью так называемых соединителей. Как известно, соединитель “используется для обрыва линии и продолжения ее в другом месте... для избежания излишних пересечений” [2].

В языке ДРАКОН все перечисленные ухищрения (пересечения, обрывы, соединители) по эргономическим соображениям считаются вредными и категорически запрещены, так как они засоряют поле чертежа ненужными деталями, создают визуальные помехи для глаз и отвлекают внимание от главного.

Поскольку запрет пересечений является серьезным топологическим ограничением, возникает вопрос: можно ли произвольный алгоритм изобразить в виде дракон-схемы?

Теорема 1. Любая структурная программа может быть изображена
на языке ДРАКОН двумя способами: в виде примитива и в виде силуэта.

Теорема 2. Произвольная (неструктурная) программа в ряде случаев
не может быть изображена в виде примитива; однако с помощью
эквивалентных преобразований, допускающих введение дополни­тельных переменных (идентификаторов ветки), она всегда может быть изображена в виде силуэта.

Чтобы прояснить вопрос, обратимся к примерам. На рис. 13 а приведена запрещенная дракон-схема: примитив, в котором имеется неустранимое (без введения дополнительных переменных) пересечение. На рис. 13 б изображен силуэт, который, как нетрудно убедиться, эквивалентен примитиву на рис. 13 а и вместе с тем не содержит ни одного пересечения. Таким образом, пример на рис. 13 подтверждает справедливость теоремы 2[15].

Подведем итоги. Язык ДРАКОН обладает важным достоинством: он позволяет изобразить любой алгоритм, полностью отказавшись от таких эргономически неудачных приемов, как пересечения, обрывы, соединители. Отсутствие “паразитных элементов” создает дополнительные удобства для читателя, делает дракон-схему прозрачной, облегчает понимание.

ВИЗУАЛЬНЫЙ И ТЕКСТОВЫЙ
СИНТАКСИС ДРАКОНА

ДРАКОН — визуальный язык, в котором используются два типа элементов: графические фигуры (графоэлементы) и текстовые надписи, расположенные внутри или снаружи графических фигур (текстоэлементы). Следовательно, синтаксис ДРАКОНА распадается на две части. Визуальный синтаксис охватывает алфавит графоэлементов, правила их размещения в поле чертежа и правила связи графоэлементов с помощью соединительных линий. Текстовый синтаксис задает алфавит символов, правила их комбинирования и привязку к графоэлементам (привязка необходима потому, что внутри разных графических фигур используются разные типы выражений). Оператором языка ДРАКОН является графоэлемент или комбинация графоэлементов, взятые вместе с текстовыми надписями.

Одновременное использование графики и текста говорит о том, что ДРАКОН адресуется не только к словесно-логическому мышлению автора и читателя программы, но сверх того активизирует интуитивное, образное, правополушарное мышление, стимулируя его не написанной, а именно нарисованной программой, т. е. программой-картинкой.

СЕМЕЙСТВО ДРАКОН-ЯЗЫКОВ

ДРАКОН — не один язык, а целое семейство, все языки которого имеют одинаковый визуальный синтаксис (что зрительно делает языки семейства почти близнецами) и отличаются текстовым синтаксисом.

ДРАКОН-1 — визуальный псевдоязык, визуальный аналог обычного текстового псевдокода. Он служит для описания структуры деятель­ности, создания технологий, алгоритмов и проектов программ, используется в методе пошаговой детализации, а также при формализации профессиональных знаний.

ДРАКОН-2 — язык визуального программирования реального времени. Он является элементом CASE -технологии для разработки программного обеспечения систем управления ракет и космических объектов, а также атомных электростанций, нефтехимических и металлургических заводов, биотехнологических производств и т. д.

Кроме того, семейство включает гибридные визуальные языки программирования: ДРАКОН-БЕЙСИК, ДРАКОН-ПАСКАЛЬ, ДРАКОН-СИ
и т. д. Чтобы получить гибридный язык, например, ДРАКОН-СИ, необходимо взять визуальный синтаксис ДРАКОНА и присоединить к нему по определенным правилам текстовый синтаксис языка СИ.

Строгое разграничение визуального и текстового синтаксиса позволяет в максимальной степени расширить сферу применения языка, обеспечивая его гибкость и универсальность. При этом единообразие правил визуального синтаксиса семейства ДРАКОН-языков обеспечивает их концептуальное единство, а разнообразие текстовых правил (т. е. возможность выбора любого текстового синтаксиса) определяет гибкость языка и легкую настройку на различные проблемные и предметные области.

В настоящей книге основное внимание уделяется визуальному псевдоязыку ДРАКОН-1. Что касается остальных языков ДРАКОН-семейства, даются лишь краткие пояснения.

ВЫВОДЫ

Приведем сводку эргономических правил, позволяющих улучшить когнитивное качество дракон-схем и сделать алгоритмы, программы и технологии более понятными.

1. Сложный алгоритм следует рисовать в виде силуэта, простой — в виде примитива.

2. В иконе “заголовок” запрещается писать слово “начало”; вместо этого следует указать понятное и точное название алгоритма.

3. Разбейте сложный алгоритм на части, каждую часть изобразите в виде ветки. Дайте частям доходчивые и четкие названия и запишите их в иконах “имя ветки”.

4. Вход в ветку возможен только через ее начало.

5. В иконе “адрес” разрешается писать имя одной из веток, другие надписи запрещены.

6. Ветки следует располагать в пространстве согласно правилу: чем правее, тем позже. Наличие веточного цикла модифицирует это правило.

7. Примитив обязательно имеет шампур. Это значит, что у примитива иконы “заголовок” и “конец” всегда лежат на одной вертикали, которая и называется “шампур”.

8. Каждая ветка обязательно имеет шампур. У правой ветки шампур — это вертикаль, соединяющая иконы “имя ветки” и “конец”. У остальных веток шампуром служит вертикальная линия, соединяющая иконы “имя ветки” и “адрес”, а если адресов несколько — с левым из них.

9. Алгоритм всегда имеет главный маршрут, который должен идти по шампуру.

10. Побочные маршруты должны быть упорядочены слева направо
согласно одному из выбранных критериев, например: чем правее — тем хуже.

11. В иконе “конец” следует писать слово “конец”.

12. Соединительные линии могут идти либо горизонтально, либо вертикально. Наклонные линии не допускаются.

13. Пересечения линий запрещены.

14. Обрывы линий запрещены.

15. Использование соединителей запрещено.

 

 

Г Л А В А 7

Эргономичные алгоритмы

На ошибках мы горим! —
Мне сказал Алеха.
Непонятный алгоритм —
Это очень плохо.

Мы ошибки победим!
Надо сделать вот чего —
Надо сделать алгоритм
Ясным и доходчивым!

Юрий Примашев

ВИЗУАЛЬНАЯ ПРОВЕРКА АЛГОРИТМОВ

При решении сложных задач, таких как предсказание погоды, управление войсками, управление большой электростанцией или нефтехимическим заводом, приходится создавать крупномасштабные алгоритмы, насчитывающие сотни тысяч и даже миллионы команд. Практика показывает: чем крупнее алгоритмы, тем больше в них ошибок, тем сложнее их найти. Исправлять ошибки в огромных и сложных алгоритмах — трудное и дорогостоящее занятие, причем цена ошибки тем выше, чем позже она обнаружена.

Наименьший ущерб приносят ошибки, которые удается обнаружить сразу, до генерации кода и исполнения программы на компьютере — в ходе мозговой или, что одно и то же, визуальной проверки. Проверка называется мозговой, если главная работа по поиску ошибок выпол­няется благодаря интеллектуальным усилиям человека, а компьютер играет хотя и важную, но вспомогательную роль. При такой проверке человек тщательно изучает компьютерные чертежи спецификаций и алгоритмов, представленные на бумаге или экране.

Мозговую проверку, как и любую другую деятельность, нужно грамотно проектировать. Критерием ее эффективности служит минимизация средних интеллектуальных усилий мозга, затрачиваемых на выявление одной ошибки. Нейронная конструкция мозга такова, что он может эффективно проводить визуальную проверку отнюдь не при любых условиях, а только в том случае, если проверяемые чертежи обладают высоким когнитивным качеством. Чтобы минимизировать удельные интеллектуальные усилия, необходимо, чтобы когни­тивно-значимые характеристики чертежей были хорошо согласованы
с конструктивными характеристиками мозга. Это значит, что спецификации и алгоритмы должны быть специально приспособлены для быстрой и надежной проверки, для легкого и вместе с тем глубокого понимания.

ЧТО ТАКОЕ ЭРГОНОМИЧНЫЙ АЛГОРИТМ?

В связи с этим полезно ввести понятие эргономичный алгоритм, т. е. алгоритм, удовлетворяющий критерию сверхвысокой понимаемости. Преимущество эргономичных алгоритмов в том, что они намного понятнее, яснее, нагляднее и доходчивее, чем обычные. Если алгоритм непонятный, в нем трудно или даже невозможно заметить затаившуюся ошибку. И наоборот, чем понятнее алгоритм, тем легче найти дефект. Поэтому более понятный, эргономичный алгоритм намного лучше обычного. Лучше в том смысле, что он облегчает выявление ошибок, а это очень важно. Ведь чем больше ошибок удастся обнаружить при визуальной проверке, тем больше вероятность, что вновь созданный алгоритм окажется правильным, безошибочным, надежным. Кроме того, эргономичные алгоритмы удобнее для изучения, их проще объяснить другому человеку.

В предыдущей главе мы рассмотрели несколько способов, позволяющих улучшить эргономические характеристики алгоритмов. В этой главе, продолжая тему, попытаемся ответить на вопрос: можно ли повысить эргономичность алгоритмов, используя формальный метод эквивалентных преобразований?

Для этого понадобится особый понятийный аппарат, заметно отличающийся от того, которым обычно пользуются программисты, так как традиционные понятия плохо приспособлены для решения проблемы понимания и совершенно не учитывают специфику визуальных образов.

ЧЕМ ОТЛИЧАЕТСЯ ИКОНА “ВОПРОС”
ОТ РАЗВИЛКИ?

На рис. 1 (позиция И4) изображена икона “вопрос”. Она называется так, потому что внутри нее пишут “ да-нетный ” вопрос, т. е. вопрос, на который можно ответить либо “да”, либо “нет”. Все другие ответы запрещены. Вот примеры да-нетных вопросов: утюг сломался? Тетя при­ехала? Вася купил хлеб? Преступника арестовали? Эта лужа больше, чем та? Температура выше нуля?

Икона “вопрос” имеет один вход сверху и два выхода: вниз и вправо. Выход влево запрещен и никогда не используется.

На рис. 2 (позиция 2) показана макроикона “развилка”. Она содержит икону “вопрос”, точку слияния и два плеча: левое и правое (рис. 14 б). Левое плечо есть путь от нижнего выхода иконы-вопроса до точки слияния. Правое плечо начинается у правого выхода иконы-вопроса и заканчивается в точке слияния (рис. 15). Таким образом, плечо имеет в своем составе надпись “да” или “нет”, соединительные линии, точку слияния, а также иконы. Одно из двух плеч может быть пустым (не содержать икон).

Развилки бывают простые и сложные. Простая развилка содержит только одну икону-вопрос. Примеры простых развилок показаны на рис. 16. Развилка называется сложной, если в ее плечах имеется по

крайней мере одна простая развилка. На рис. 10 а показаны три сложные развилки. Например, развилка “Борщ очень вкусный?” сложная, так как ее левое плечо содержит простую развилку “Борщ сильно пересолен?”. Другие примеры сложных развилок показаны на рис. 17.

МАРШРУТЫ И ФОРМУЛЫ МАРШРУТОВ

На рис. 18 а представлена дракон-схема “Охота на мамонта”. Заменим текст внутри икон буквами. Вместо “Охота на мамонта” запишем букву А, вместо “Поймай мамонта” — букву Б и т. д. В результате получим литеральную (буквенную) дракон-схему на рис. 18 б. Литеральные схемы удобно использовать для описания маршрутов.

Маршрут — это графический путь от начала до конца алгоритма, проходящий через иконы и соединительные линии. Маршрут можно описать с помощью формулы, которая представляет собой последова­тельность букв, обозначающих иконы. Все иконы, включая одинаковые, обозначаются разными буквами.

Линейный (неразветвленный) алгоритм имеет только один маршрут и одну формулу. Например, схема на рис. 18 б описывается формулой

Разветвленный алгоритм имеет несколько (два или более) маршрутов, причем у каждого маршрута своя, отличная от других формула (рис. 19, 20). В формулах разветвленных алгоритмов наряду с буквами, обозначающими иконы, используются слова “да” или “нет” (отделяемые пробелами).

ЧТО ТАКОЕ РОКИРОВКА?

Рокировка — это преобразование алгоритма, при котором левое и правое плечо развилки меняются местами. Простейшие примеры рокировки показаны на рис. 8 и 21.

Два алгоритма называются равносильными, если для каждого маршрута первого алгоритма можно найти парный маршрут второго алгоритма, причем для каждой пары маршрутов их формулы совпадают. Обратимся к рис. 22. Легко убедиться, что схемы на рис. 22 а и б имеют одинаковый набор маршрутов:

Следовательно, указанные дракон-схемы равносильны.

Формальное преобразование алгоритма А1 в алгоритм А2 назы­вается равносильным, если алгоритмы А1 и А2 равносильны. Сказанное означает, что рокировка является равносильным преобразованием алгоритмов. При рокировке слова “да” и “нет” обязательно меняются местами.

18-20

21-22

ИСПОЛЬЗОВАНИЕ РОКИРОВКИ
ДЛЯ УЛУЧШЕНИЯ ЭРГОНОМИЧНОСТИ

Мы убедились, что рокировка алгоритма на рис. 8 а позволила получить алгоритм на рис. 8 б, который имеет более высокие эргономические характеристики, так как на рис. 8 б соблюдается правило “главный маршрут идет по шампуру”. Это означает, что равносильное преобразо­вание “рокировка” в примере на рис. 8 действительно улучшает эргономичность алгоритма.

Попытаемся обосновать аналогичный вывод для рис. 21, рассмотрев последовательно все промежуточные шаги рассуждений.

На первом шаге выдвигаем гипотезу: для сравнения двух маршрутов на рис. 21 а можно использовать признак “лучше—хуже”.

На втором шаге проверяем гипотезу с помощью рассуждений: если брюки впору — это хорошо, если их приходится подворачивать — это плохо. Следовательно, использование в данном алгоритме признака “лучше—хуже” правомерно.

На третьем шаге определяем главный маршрут, который по соглашению соответствует признаку “хорошо”. Следовательно, главный маршрут на рис. 21 а идет через правое плечо развилки, что соответствует хорошей ситуации “брюки впору — их не надо подворачивать”.

На четвертом шаге констатируем, что главный маршрут на рис. 21 а не идет по шампуру. Делаем вывод: алгоритм на рис. 21 а является плохим, неэргономичным, однако его можно исправить с помощью рокировки.

На пятом шаге выполняем рокировку и получаем более эргономичный алгоритм на рис. 21 б. На этом процедура заканчивается[16].

Рассмотрим теперь более сложный алгоритм на рис. 10 а. Этот алгоритм тоже плохой, потому что содержит три плохие (неэргономичные) развилки: 1) “В меню есть твой любимый салат?”, 2) “Борщ очень вкусный?”, 3) “Жаркое, как подошва?”. Последовательно применяя к развилкам три операции “рокировка”, получаем эргономичный алгоритм на рис. 10 б.

Таким образом, на основании анализа примеров мы убедились: равносильное преобразование “рокировка” позволяет улучшить эргономичность алгоритмов. Однако этот вывод относится только к смысловым алгоритмам (где можно указать главный маршрут) и неприменим
к литеральным алгоритмам (где понятие главного маршрута теряет
силу). Отсюда вытекает, что применение рокировки к литеральной схеме на рис. 22 бессмысленно, так как в данном случае рокировка не влияет на эргономичность.

ВЕРТИКАЛЬНОЕ И ГОРИЗОНТАЛЬНОЕ
ОБЪЕДИНЕНИЕ

Бывает, что в дракон-схемах одинаковые иконы повторяются несколько раз. Например, на рис. 23 а икона “Отдай мотоцикл в ремонт и впредь будь умнее” встречается три раза. Это плохо: навязчивые повторения раздражают читателя, которому приходится тратить лишнее время и несколько раз читать одно и то же. К счастью, некоторые повторы можно устранить. Такая возможность появляется, если одинаковые иконы соседствуют друг с другом, причем их выходы соединены между собой (рис. 23 а). В этом случае действует правило “повторы запрещены”. Устранение повторов производится с помощью вертикальной линии (рис. 23 б) и называется вертикальным объединением. Нетрудно доказать, что операция “вертикальное объединение” осуществляет равносильное преобразование алгоритмов.

Название “объединение” объясняется тем, что несколько одинаковых икон объединяются в одну. Последовательность действий такова: сначала входы этих икон объединяются вертикальной линией, после чего удаляются все одинаковые иконы, кроме крайней левой.

Сравнивая алгоритмы на рис. 23 а и б, легко заметить, что схема на рис. 23 б обладает более высоким эргономическим качеством: она стала более компактной, ясной и наглядной, поскольку освободилась от бессмысленного повторения икон. Отсюда проистекает вывод: равносильное преобразование “вертикальное объединение” позволяет улучшить эргономичность алгоритмов.

Иногда для исключения повторов используется не вертикальная, а горизонтальная линия. Соответствующая операция называется горизонтальным объединением. Она также является равносильным преобразованием.

Рассмотрим пример на рис. 24 а. Сначала с помощью горизонтального объединения устраним повторение иконы “Съешь кашу” и получим схему на рис. 24 б. Затем применим вертикальное объединение и исключим повторение развилки “Есть можно?”. Окончательный результат показан на рис. 24 в. Полученная схема более удобна и занимает меньше места, чем исходная схема на рис. 24 а.