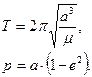I. Теоретические сведения.
Это уравнение тождественно такому: Интегрируя уравнение (9), получаем интеграл площадей в векторной форме:
где постоянная интегрирования
. Вычёркивая первый ряд в матрице (11) и колонку соответствующего орта, получаем определители второго порядка, вычисляя которые, получаем три интеграла площадей в координатной форме: Название интеграла площадей происходит из сущности векторного произведения, результатом которого есть вектор Интеграл энергии. Векторное дифференциальное уравнение невозмущённого движения (5) умножим скалярно на 2
Левая часть уравнения (13) тождественна выражению: Кроме того, справедливо тождество: Подставляя (14) и (14) в (13), получаем:
Известно, что: Подставив тождества (17) в (16) и проинтегрировав, имеем: где Интегралы Лапласа. Дифференциальные уравнения невозмущённого движения умножим векторно на интеграл площади
Интеграл площадей с в соответствии с (10) является результатом векторного произведения векторов
Векторное произведение трёх векторов можно заменить скалярным в соответствии с правилом: Сделав эту замену в уравнении (20), имеем: После преобразований имеем: Это выражение тождественно такому:
Интегрируя (21), получаем интеграл Лапласа в векторной форме:
где
Записывая векторное произведение через определители, и приравнивая выражения при одинаковых ортах, получаем интегралы Лапласа в интегральной форме:
где составляющие вектора Лапласа
Что свидетельствует про взаимную перпендикулярность векторов
где Исследования невозмущённого движения. Если векторные уравнения интеграла площадей (10) скалярно умножить на вектор
которое оказывается уравнением плоскости, проходящей через начало координат. В координатной форме оно имеет такой вид:
Уравнения (26) или (27) показывают, что невозмущённое движение осуществляется в неизменной плоскости, которая определяется только начальными условиями задачи и, как следствие, орбита ИСЗ есть плоская кривая. Отсюда, невозмущённое движение происходит в плоскости, которая перпендикулярна (ортогональна) к вектору площади с. Из математики известно, что положение плоскости в пространстве определяется перпендикулярным (ортогональным) к ней вектором. Таким образом, вектор площади с определяет ориентацию плоскости орбиты спутника в пространстве. Теперь на вектор
а в координатной форме оно имеет такой вид:
Уравнения (28) или (28´) описывает поверхность на которой находится спутник во время движения. Эта поверхность является поверхностью второго порядка, образованная вращением вокруг оси, которая задана вектором
геометрически является сечение плоскостью поверхности вращения. В результате сечения получается плоская кривая второго порядка. В соответствие с первым законом Кеплера невозмущённая орбита искусственного небесного тела является плоскою кривой второго порядка в одном из фокусов которой размещено центральное тело (для искусственных спутников Земли центральным телом является Земля). В зависимости от вида эксцентриситета орбита этого тела может принимать форму одной из таких плоских кривых второго порядка: - Круга, если эксцентриситет е = 0; - Эллипса, если эксцентриситет 0 < е < 1; - Параболы, если эксцентриситет е = 1; - Гиперболы, если эксцентриситет е > 1. Орбита ИСЗ может быть также кругом. Форма, размеры, ориентация эллиптической орбиты спутника определяются 6-ю параметрами (элементами отбиты), а именно:
Рис.1. Угловые элементы орбиты
Размеры и форму орбиты задают большей полуосью Орбита спутника пересекает экватор в двух точках. Эти точки называются узлами: восходящий Долгота восходящего узла измеряется от точки весеннего равноденствия по экватору от 0˚ до 360˚, а угол наклона от плоскости экватора до плоскости орбиты от 0˚ до 180˚. Аргумент перицентра (для ИСЗ – перигея) Положение спутника на орбите определяется угловым параметром Прямая, соединяющая фокусы – линия аспид, совпадает с направлением вектора Лапласа, а вектор площадей перпендикулярен к плоскости орбиты (рис.2)
Рис.2 Орбита ИСЗ и взаимное размещение векторов Движение спутника по орбите описывают второй и третий законы Кеплера. Во втором законе Кеплера говорится, что за равные промежутки времени радиус-вектор спутника описывает равные площади. Другими словами секториальная скорость является постоянной. Это можно вывести, если рассматривать движение ИСЗ в системе координат
Рис. 3. Связь систем координат В выбранной орбитальной системе координат (рис. 3) интегралы площадей получаем из выражения:
где
Введём полярную систему координат в плоскости орбиты через радиус-вектор
Теперь подставим выражения (32) в (31) для вектора площадей и после преобразований получим:
Пусть положение спутника за небольшой промежуток
Производную от площади по времени
Сравнивая формулы (33) и (34) имеем:
Формула (35) выражает второй закон Кеплера. Уравнение орбиты в полярных координатах. Решение системы уравнений (29) является уравнением орбиты. В орбитальной системе координат система (29) преобразовывается в такую:
В полярных координатах второе уравнение (36) после подстановки
Если обозначить
получим уравнение кривой второго порядка в полярных координатах:
где
В зависимости от эксцентриситета е плоская кривая второго порядка может приобретать разные формы и значения интегралов
При эллиптическом движении 0 < e < 1, тогда на основании (40)
Это означает, что кинетическая энергия движения меньше его потенциальной энергии. Если е = 0, из (40) имеем:
Во время кругового движения радиус орбиты
Если принять, что Земля имеет сферическую форму с радиусом 6371,1 км и При параболическом движении е = 1, поэтому
Таким образом при параболическом движении кинетическая и потенциальная энергии искусственного небесного тела одинаковы, а для Земли это выполняется при скорости спутника В теории движения ИСЗ принято круговую скорость космического аппарата называть первой космической скоростью, а параболическую – второй космической скоростью. При гиперболическом движении е > 1 и
В этом выражении определяющую роль играет кинетическая энергия спутника, она больше потенциальной энергии. Динамический интеграл. Все полученные ранее интегралы (12), (18) и (23) не являются общим решением системы дифференциальных уравнений невозмущённого движения (6), потому, что не содержат время в явном виде. Интеграл, который даёт в явном виде зависимость положения ИСЗ на орбите от времени
Интеграл в левой части выражения (45) зависит от того, какое значение имеет эксцентриситет орбиты е. Поскольку ИСЗ, как правило, имеет эллиптическую орбиту
После дифференцирования (46), подстановки в (45) и интегрирования получаем:
Введём среднее движение
Уравнение (47) с учётом (48) и (49) приобретает вид:
Это уравнение называется уравнением Кеплера. Оно связывает вспомогательную переменную, какой является эксцентрическая аномалия Е, среднюю аномалию М, момент прохождения спутника через перигей В соответствии с (49) средняя аномалия М возрастает прямо пропорционально времени и определяет положение некоторого фиктивного спутника, который равномерно движется по кругу радиуса большей полуоси а с периодом Т, который равен периоду реального ИСЗ. Реальный спутник движется по эллипсу и в соответствии со вторым законом Кеплера имеет максимальную скорость в перигее и минимальную скорость в апогее. Пусть спутник имеет период обращения Т. Тогда из (49) и (50) следует, что при полном обороте спутника получаем
где, Подставим в (51) вместо
Это формула отображает третий закон Кеплера, согласно с которого в эллиптическом невозмущённом движении отношение квадрата периода Т обращения спутника по орбите к кубу её большой полуоси есть постоянным для данной планеты. Движение ИСЗ по законам Кеплера являются наипростейшей моделью орбитального движения спутника и называется кеплеровским или невозмущённым движением. Необходимым условием выполнения законов Кеплера является допущение, что Земля (центральное тело) и спутник – это материальные точки с массами, равными массам Земли и спутника соответственно. В таком случае спутник движется по инерции, под действием приданного ему начального импульса и только одной силы – силы гравитационного притяжения Земли. II. Содержание работы. В соответствии со сказанным ранее, за модель Земли принимаем шар со средним радиусом Задача 1. Построить схематично эллиптическую орбиту и её проекцию на небесную сферу по параметрам: - долготой восходящего узла орбиты - углом наклона орбиты - аргументом перицентра и показать положение спутника на орбите, если известна его аномалия Результатом этой задачи должен быть схематически построенный чертёж, на котором по данным своего варианта (параметрами орбиты Задача 2. Для ИСЗ на околоземной орбите вычислить три из четырёх величин: радиус орбиты а. известна высота орбиты б. задано среднее движение в. известен период обращения Формулы для решения задачи. Случай а. Если известна высота орбиты Н, то можно вычислить радиус круговой орбиты По известному радиусу орбиты получаем линейную скорость спутника по (42)
Для круговой орбиты имеем е = 0, отсюда большая полуось, а равна радиусу орбиты,
Отсюда вычисляем период обращения спутника Т:
По результатам вычислений необходимо сделать рисунок, на котором показать: Землю в виде сферы и круговую орбиту ИСЗ. За единицу масштаба принять радиус Земли
Отсюда период обращения спутника По известному периоду из третьего закона Кеплера получаем большую полуось орбиты: Поскольку орбита круговая, то
По результатам вычислений необходимо сделать рисунок, подобный случаю а. Случай в. Формулы и ход решения этой задачи такие же как и в предыдущей, за исключением первой формулы, потому, что период обращения ИСЗ уже известен. Только одно замечание: перед вычислением большой полуоси орбиты спутника по (55) необходимо период Т движения ИСЗ, заданный в часах, минутах и секундах По результатам вычислений необходимо сделать рисунок, подобный случаю а.
Задача 3. Для ИСЗ, который находится на эллиптической орбите, необходимо вычислить: период Т, радиус-вектор Формулы для решения задачи.
где р – фокальный параметр.
К задаче необходимо сделать рисунок, на котором угол истинной аномалии должен соответствовать значению, заданному в исходных данных.
|

 (9)
(9) (10)
(10) является вектором интеграла площадей. Векторное произведение (10) в матричной форме имеет такой вид:
является вектором интеграла площадей. Векторное произведение (10) в матричной форме имеет такой вид: , (11)
, (11) (12)
(12) и
и  . Направление вектора
. Направление вектора  и
и  .
. (13)
(13) (14)
(14) (15)
(15) (16)
(16)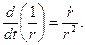 (17)
(17)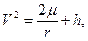 (18)
(18)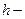 постоянная интегрирования. Умножив (18) на
постоянная интегрирования. Умножив (18) на  получаем
получаем  запас кинетической энергии,
запас кинетической энергии, 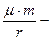 потенциальная энергия
потенциальная энергия  полный запас механической энергии системы. Таким образом
полный запас механической энергии системы. Таким образом  характеризует распределение энергии на кинетическую и потенциальную, в зависимости от положения спутника на орбите, а также постоянство общей алгебраической суммы кинетической и потенциальной энергии в системе Земля – спутник. Поэтому (18) называют интегралом энергии, а его постоянную
характеризует распределение энергии на кинетическую и потенциальную, в зависимости от положения спутника на орбите, а также постоянство общей алгебраической суммы кинетической и потенциальной энергии в системе Земля – спутник. Поэтому (18) называют интегралом энергии, а его постоянную  получим:
получим: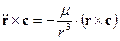 (19)
(19) В правой части (19), заменив вектор с, получим:
В правой части (19), заменив вектор с, получим: (20)
(20)


 (21)
(21) (22)
(22) постоянная интегрирования, которая называется вектором Лапласа. Обозначив его составляющие через
постоянная интегрирования, которая называется вектором Лапласа. Обозначив его составляющие через  (22) можно записать в виде, который раскрывает векторное произведение:
(22) можно записать в виде, который раскрывает векторное произведение:
 (23)
(23) являются постоянными этих интегралов или постоянными Лапласа. Формулами (12), (18) и (23) записаны семь первых интегралов невозмущённого движения ИСЗ. Но они не составляют общее решение системы (7), потому, что во-первых не являются независимыми и, во-вторых, не содержат в явном виде время
являются постоянными этих интегралов или постоянными Лапласа. Формулами (12), (18) и (23) записаны семь первых интегралов невозмущённого движения ИСЗ. Но они не составляют общее решение системы (7), потому, что во-первых не являются независимыми и, во-вторых, не содержат в явном виде время  Зависимость между этими интегралами можно выразить через произвольные постоянные уравнениями:
Зависимость между этими интегралами можно выразить через произвольные постоянные уравнениями: (24)
(24) и
и (25)
(25)
 (26)
(26)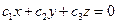 (27)
(27) (28)
(28)
 (28´)
(28´)
 большей полуосью орбиты;
большей полуосью орбиты;  эксцентриситетом орбиты,
эксцентриситетом орбиты, долготой восходящего узла орбиты,
долготой восходящего узла орбиты, углом наклона плоскости орбиты,
углом наклона плоскости орбиты, аргументом перицентра,
аргументом перицентра,
 моментом прохождения спутника через перицентр.
моментом прохождения спутника через перицентр. и эксцентриситетом
и эксцентриситетом  орбиты. Ориентацию плоскости орбиты в пространстве определяет долгота восходящего узла орбиты
орбиты. Ориентацию плоскости орбиты в пространстве определяет долгота восходящего узла орбиты  и угол наклона
и угол наклона 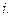
 , в котором спутник пересекает экватор, двигаясь из южного полушария в северное; нисходящий
, в котором спутник пересекает экватор, двигаясь из южного полушария в северное; нисходящий  , в котором спутник пересекает экватор, двигаясь из северного полушария в южное.
, в котором спутник пересекает экватор, двигаясь из северного полушария в южное. ориентирует большую полуось орбиты (линию аспид, которая соединяет точки апогея и перигея) в её плоскости, и измеряется от точки восходящего узла от 0˚ до 360˚. Апогей является наиболее удалённой точкой орбиты от Земли, а перигей – ближайшей.
ориентирует большую полуось орбиты (линию аспид, которая соединяет точки апогея и перигея) в её плоскости, и измеряется от точки восходящего узла от 0˚ до 360˚. Апогей является наиболее удалённой точкой орбиты от Земли, а перигей – ближайшей. истинной аномалией – углом между направлением на перигей и положением спутника (см. рис.1).
истинной аномалией – углом между направлением на перигей и положением спутника (см. рис.1).
 и
и 
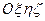 , жёстко связанной с плоскостью орбиты (рис. 3). Две оси,
, жёстко связанной с плоскостью орбиты (рис. 3). Две оси,  и
и 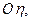 лежат в плоскости орбиты, третья направлена перпендикулярно к плоскости орбиты по вектору интеграла площадей
лежат в плоскости орбиты, третья направлена перпендикулярно к плоскости орбиты по вектору интеграла площадей  Ось
Ось 
 и
и 
 (30)
(30) орты соответствующих осей орбитальной системы координат. Раскрывая определитель и приравнивая выражения при одинаковых ортах, получаем:
орты соответствующих осей орбитальной системы координат. Раскрывая определитель и приравнивая выражения при одинаковых ортах, получаем: (31)
(31) и в этой системе координат выразим интеграл площадей (31). Для этого найдём выражения для координат
и в этой системе координат выразим интеграл площадей (31). Для этого найдём выражения для координат  и слагаемых вектора скорости
и слагаемых вектора скорости  спутника в плоскости орбиты:
спутника в плоскости орбиты: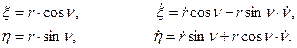 (32)
(32) (33)
(33) изменится на угол
изменится на угол  Тогда площадь, которую опишет радиус-вектор спутника, будет площадью сектора
Тогда площадь, которую опишет радиус-вектор спутника, будет площадью сектора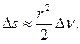
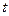 называют секториальной скоростью, которая запишется таким образом:
называют секториальной скоростью, которая запишется таким образом: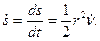 (34)
(34) (35)
(35) (36)
(36) получает вид:
получает вид:
 (37)
(37) (38)
(38) фокальный параметр кривой,
фокальный параметр кривой,  (39)
(39)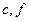 и
и  также изменяются. Рассмотрим, какие значения приобретает интеграл энергии
также изменяются. Рассмотрим, какие значения приобретает интеграл энергии  при различных эксцентриситетах е. Для этого воспользуемся уравнением связи первых семи интегралов (25), в котором, учитывая обозначения (37), получаем:
при различных эксцентриситетах е. Для этого воспользуемся уравнением связи первых семи интегралов (25), в котором, учитывая обозначения (37), получаем: (40)
(40) и из интеграла энергии следует, что:
и из интеграла энергии следует, что:
 (41)
(41) Учитывая это и подставляя (41) в интеграл энергии, получаем
Учитывая это и подставляя (41) в интеграл энергии, получаем (42)
(42) , то
, то 
 и, соответственно:
и, соответственно: (43)
(43) 11,2 км/с.
11,2 км/с. поєтому:
поєтому: (44)
(44) получаем интегрированием выражения для интеграла площадей (33). Подставляя уравнение орбитальной кривой (38), имеем:
получаем интегрированием выражения для интеграла площадей (33). Подставляя уравнение орбитальной кривой (38), имеем: (45)
(45) поэтому рассмотрим только этот случай. Чтобы вычислить интеграл (45), вводят новую переменную на основе тангенса половинного угла по формуле:
поэтому рассмотрим только этот случай. Чтобы вычислить интеграл (45), вводят новую переменную на основе тангенса половинного угла по формуле: (46)
(46) (47)
(47) и среднюю аномалию М по формулам:
и среднюю аномалию М по формулам: (48)
(48) (49)
(49)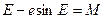 (50)
(50) и текущее время
и текущее время  отсюда:
отсюда: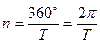 (51)
(51)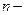 средняя угловая скорость движущейся точки. В небесной механике её называют средним движением.
средняя угловая скорость движущейся точки. В небесной механике её называют средним движением. (52)
(52) км и геоцентрической постоянной
км и геоцентрической постоянной  км3/с2. Эти параметры являются исходными для решения задач.
км3/с2. Эти параметры являются исходными для решения задач.



 и
и  ) нанесены параметры орбиты как на рис. 1.
) нанесены параметры орбиты как на рис. 1.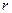 , период обращения Т, линейную скорость
, период обращения Т, линейную скорость  высоту орбиты
высоту орбиты  если одна из этих величин известна. Выполнить вычисления для таких трёх случаев:
если одна из этих величин известна. Выполнить вычисления для таких трёх случаев:

 если ИСЗ имеет геостационарную орбиту.
если ИСЗ имеет геостационарную орбиту. поскольку известен радиус
поскольку известен радиус  сферической модели Земли:
сферической модели Земли: 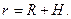 (53)
(53) Применим третий закон Кеплера для этого случая:
Применим третий закон Кеплера для этого случая:
 (54)
(54)



 , и теперь высоту орбиты Н и линейную скорость ИСЗ находят по известным формулам:
, и теперь высоту орбиты Н и линейную скорость ИСЗ находят по известным формулам:
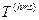 , перевести в секунды
, перевести в секунды  , т.е.
, т.е.  . далее вычисления выполняются по формулам (55) и (56).
. далее вычисления выполняются по формулам (55) и (56).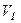 , апогея
, апогея  и в точке орбиты
и в точке орбиты  с заданной аномалией
с заданной аномалией