Комплексный чертеж точки

1. Увеличение времени внутреннего отклонения в отведениях V₁ и V₂ более 0,03 сек.

2. Увеличение амплитуды зубца R в правых отведениях: III, aVF, V₁ и V₂.

3. Смещение сегмента ST ниже изолинии, инверсия или двуфазность зубца Т в правых отведениях: III, aVF, V₁ и V₂.

4. Нарушение проводимости по правой ножке пучка Гиса: полные или неполные блокады ножки.

5. Отклонение электрической оси сердца вправо (правограмма). Электрическая позиция сердца вертикальная или полувертикальная.

6. Смещение переходной зоны в отведение V₄ или V₅.

 

Наиболее информативными являются следующие признаки гипертрофии правого желудочка:

1. смещение электрической оси сердца вправо (угол α более +100°);

2. увеличение амплитуды зубца R в правых грудных отведениях (V1, V2) и амплитуды зубца S в левых грудных отведениях (V5, V6).

3. При этом количественными критериями могут являться: амплитуда RV₁≥7 мм

4. появление в отведениях V1 комплекса QRS типа rSR или QR;

ВОПРОСЫ ДЛЯ ЗАКРЕПЛЕНИЯ

1. Назовите предсердный зубец на ЭКГ.

2. Перечислите (+) зубцы ЭКГ во II стандартном отведении при отсутствии патологии.

3. Перечислите (-) зубцы ЭКГ во II стандартном отведении при отсутствии патологии.

4. Наличие какого зубца на ЭКГ характерно для синусового ритма?

5. Что отражает комплекс QRS на ЭКГ? Сегмент ST и зубец Т?

6. Назовите электрическую систолу и электрическую диастолу сердца.

7. Назовите формулу для подсчета ЧСС по ЭКГ.

8. Диагностическое значение ЭКГ.

Комплексный чертеж точки

Комплексный чертеж состоит из двух или более связанных между собой ортогональных проекций предмета. Эти проекции получают на взаимно перпендикулярных плоскостях проекций, которые при пересечении образуют четыре двугранных угла (т.е. пространство делит на четыре части), называемые четвертями пространства. В дальнейшем изложении, построение чертежа точки в любой четверти, рассмотрены на рисунках 2.1 и 2.2, считая, что наблюдатель находится в первой четверти

Обычно одну из плоскостей проекций располагают горизонтально (рисунок 2.1,а) и называют горизонтальной плоскостью проекций - П_1. Проекции элементов пространства на ней А_1, а _1, Θ₁ называются горизонтальными проекциями (точки, прямой, плоскости).

Вторую плоскость проекций располагают перед наблюдателем вертикально. Называется эта плоскость фронтальной, обозначается П₂, а проекции на ней А₂, а ₂,Θ₂, называются фронтальными проекциями (точки, прямой, плоскости).

Плоскости проекций П₁ и П₂ взаимно перпендикулярны, их линия пересечения называется осью проекций. Точку Апространства, ортогонально проецируют на обе плоскости проекций:

 

AA₁ П₁; АА₁ Ç П₁ = А₁.

АА₂ П₂; АА₂ Ç П₂=А₂.

 

Чтобы получить плоский чертеж, совместим горизонтальную плоскость проекций П_l с фронтальной плоскостью П₂ вращением вокруг оси х ₁₂ (рисунок 2.1,б). Тогда обе проекции точки окажутся на одной линии, перпендикулярной оси х ₁₂. Прямая А₂А₁, соединяющая горизонтальную А₁ и фронтальную А₂ проекции точки, называется линией связи.

а)

б)

в)

 

Рисунок 2.1

 

Две связанные между собой ортогональные проекции точки однозначно определяют ее положение относительно плоскостей проекций. Если определить положение точки А относительно этих плоскостей (рисунок 2.1, а) ее высотой z_A=AA₁, глубиной y_A=AA₂, то эти величины на комплексном чертеже существуют как отрезки линии связи (рисунок 2.1, в). Это обстоятельство позволяет легко реконструировать чертеж, т.е. определить по чертежу положение точки относительно плоскостей проекций. Для этого достаточно в точке А ₂ чертежа восставить перпендикуляр к плоскости чертежа (считая ее фронтальной) длиной, равной глубине z_A и из точки А₁ восставить перпендикуляр к плоскости чертежа (считая её горизонтальной) длиной равной высоте z_A. Пересечение двух перпендикулярных прямых определит положение точки А относительно плоскостей чертежа.

Положение проекций точек на эпюре зависит от того, в какой четверти находится данная точка. Так, если точка Врасположена во второй четверти (рисунок 2.2), после совмещения плоскостей обе проекции окажутся лежащими над осью x ₁₂ (рисунок 2.3).

 

Рисунок 2.2

 

Если точка С находится в третьей четверти, то ее горизонтальная проекция после совмещения плоскостей окажется над осью, а фронтальная – под осью х₁₂. Наконец, если точка Dрасположена в четвертой четверти, то обе проекции ее окажутся под осью х ₁₂. На рисунках 2.2 и 2.3 показаны точки М и N, лежащие на плоскостях проекций. При таком положении точка совпадает с одной из своих проекций, другая же её проекция - оказывается лежащей на оси х₁₂. Эта особенность отражена и в обозначении: около той проекции, с которой совпадает сама точка, пишется заглавная буква без индекса. Следует отметить и тот случай, когда обе проекции точки совпадают.

Так будет, если точка находится во второй или четвертой четверти на одинаковом расстоянии от плоскостей проекций. Обе проекции совпадают если точка расположена на оси х ₁₂. Может возникнуть необходимость в построении еще одного изображения предмета на третьей – профильной плоскости проекций П_з.

 

 

Рисунок 2.3

 

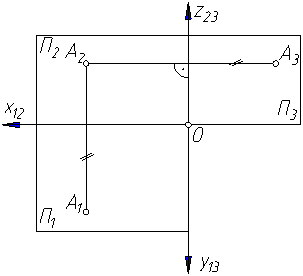
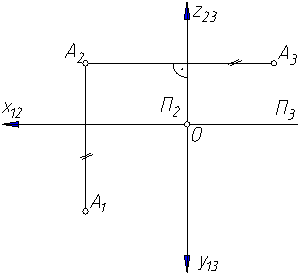
Эту плоскость располагают справа от наблюдателя перпендикулярно одновременно горизонтальной П₁ и фронтальной П₂ плоскостям проекций (рисунок 2.4, а). Линия пересечения плоскостей П₂ и П₃ – новая ось проекций – z, которая располагается на плоском чертеже (рисунок 2.4, б,в) параллельно вертикальной линии связи A₁A₂. Третья проекция точки А₃ – профильная, оказывается связанной с фронтальной проекцией А₂ новой линией связи – горизонтальной. Причем, А₂А₃ A₂А₁ и А₂А₃ z. Так как глубина точки АА₂ проецируется без искажения и на плоскость П₁,и на плоскость П₃ (рисунок 2.4, а), то это обстоятельство позволяет построить профильную проекцию точки по ее горизонтальной и фронтальной проекциям (рисунок 2.4,в). Для этого через фронтальную проекцию точки А₂ нужно провести горизонтальную линию связи А₂А₃ A₂А₁. Затем в любом месте на чертеже провести ось проекций А₂А₃ z. Измерить глубину y_A точки на горизонтальном поле проекций и отложить ее по горизонтальной линии связи от оси проекций z. Получим профильную проекцию А₃ точки А.

Таким образом, на комплексном чертеже, состоящем из трех ортогональных проекций точки, две проекции находятся на одной линии связи; линии связи перпендикулярны соответствующим осям проекций; две проекции точки вполне определяют положение ее третьей проекции. Профессором Колотовым введена постоянная прямая комплексного чертежа, которая является биссектрисой четвертого координатного угла и обозначается k123 (см. рисунок 2.4), третья проекция находится при помощи ломаной линии связи пересекающую k123.

 

а)

б)

в)

 

Рисунок 2.4