Сбор вертикальных нагрузок, действующих на обрезы фундаментов сооружения в характерных сечениях
| № п.п.
| Наименование нагрузок
| Нормативные значения нагрузок Xn, кН
| Расчетное значение нагрузки X = gn ·gf ·y2·Xn для расчета
| | по II предельному состоянию –
по деформациям
| по I предельному состоянию –
по несущей способности
| | коэф-ты gn,gf,y2
| величина нагрузки
XII, кН
| коэф-ты gn,gf,y2
| величина нагрузки
XI, кН
| |
|
|
|
|
|
|
| | СЕЧЕНИЕ 1-1 (средняя центрально нагруженная колонна в бесподвальной части здания)
| | I. ПОСТОЯННО ДЕЙСТВУЮЩИЕ НАГРУЗКИ
|
|
|
|
| |
| Собственный вес колонн
|  
| gn = 0,95
gf = 1
| 
| gn = 0,95
gf = 1,1
| 
| |
| Собственный вес ригелей перекрытий
| 
| gn = 0,95
gf = 1
| 
| gn = 0,95
gf = 1,1
| 
| |
| Собственный вес плит перекрытий
и покрытия
| 
| gn = 0,95
gf = 1
| 
| gn = 0,95
gf = 1,1
| 
| |
| Собственный вес кровли
| 
| gn = 0,95
gf = 1
| 
| gn = 0,95
gf = 1,2
| 
| | II. ВРЕМЕННЫЕ КРАТКОВРЕМЕННО ДЕЙСТВУЮЩИЕ НАГРУЗКИ
|
|
| |
| Полезная нагрузка на перекрытия
| 
| gn = 0,95
gf = 1
y2 = 0,9
| 
| gn = 0,95
gf = 1,2
y2 = 0,9
| 
| |
| Вес людей и материалов в зоне ремонта покрытия
| 
| gn = 0,95
gf = 1
y2 = 0,9
| 
| gn = 0,95
gf = 1,2
y2 = 0,9
| 
| |
| Снеговая нагрузка на покрытие
| 
| gn = 0,95
gf = 1
y2 = 0,9
| 
| gn = 0,95
gf = 1,4
y2 = 0,9
| 
| | ВСЕГО нагрузка на обрез фундамента в сечении 1-1
|  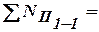
| 
|
Продолжение таблицы _____
|
|
|
|
|
|
|
| | СЕЧЕНИЕ 2-2 (внутренняя несущая стена в бесподвальной части здания)
| | I. ПОСТОЯННО ДЕЙСТВУЮЩИЕ НАГРУЗКИ
|
|
|
|
| |
| Собственный вес стены
| 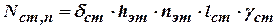
| gn = 0,95
gf = 1
| 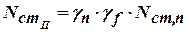
| gn = 0,95
gf = 1,2
| 
| |
| Собственный вес плит перекрытий
и покрытия
| 
| gn = 0,95
gf = 1
| 
| gn = 0,95
gf = 1,1
| 
| |
| Собственный вес кровли
| 
| gn = 0,95
gf = 1
| 
| gn = 0,95
gf = 1,2
| 
| | II. ВРЕМЕННЫЕ КРАТКОВРЕМЕННО ДЕЙСТВУЮЩИЕ НАГРУЗКИ
|
|
| |
| Полезная нагрузка на перекрытия
| 
| gn = 0,95
gf = 1
y2 = 0,9
| 
| gn = 0,95
gf = 1,2
y2 = 0,9
| 
| |
| Вес людей и материалов в зоне ремонта покрытия
| 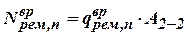
| gn = 0,95
gf = 1
y2 = 0,9
| 
| gn = 0,95
gf = 1,2
y2 = 0,9
| 
| |
| Снеговая нагрузка на покрытие
| 
| gn = 0,95
gf = 1
y2 = 0,9
| 
| gn = 0,95
gf = 1,4
y2 = 0,9
| 
| | ВСЕГО нагрузка на обрез фундамента в сечении 2-2
|  
| 
| | СЕЧЕНИЕ 3-3 (внутренняя несущая стена в части здания с подвалом)
| | I. ПОСТОЯННО ДЕЙСТВУЮЩИЕ НАГРУЗКИ
|
|
|
|
| |
| Собственный вес стены подвала
| 
| gn = 0,95
gf = 1
| 
| gn = 0,95
gf = 1,2
| 
| |
| Собственный вес стены
| 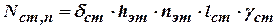
| gn = 0,95
gf = 1
| 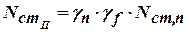
| gn = 0,95
gf = 1,2
| 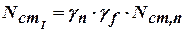
|
Продолжение таблицы _____
|
|
|
|
|
|
|
| |
| Собственный вес плит перекрытий
и покрытия
| 
| gn = 0,95
gf = 1
| 
| gn = 0,95
gf = 1,1
| 
| |
| Собственный вес кровли
| 
| gn = 0,95
gf = 1
| 
| gn = 0,95
gf = 1,2
| 
| | II. ВРЕМЕННЫЕ КРАТКОВРЕМЕННО ДЕЙСТВУЮЩИЕ НАГРУЗКИ
|
|
| |
| Полезная нагрузка на перекрытия
| 
| gn = 0,95
gf = 1
y2 = 0,9
| 
| gn = 0,95
gf = 1,2
y2 = 0,9
| 
| |
| Вес людей и материалов в зоне ремонта покрытия
| 
| gn = 0,95
gf = 1
y2 = 0,9
| 
| gn = 0,95
gf = 1,2
y2 = 0,9
| 
| |
| Снеговая нагрузка на покрытие
| 
| gn = 0,95
gf = 1
y2 = 0,9
| 
| gn = 0,95
gf = 1,4
y2 = 0,9
| 
| | ВСЕГО нагрузка на обрез фундамента в сечении 3-3
|  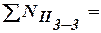
| 
| | СЕЧЕНИЕ 5-5 (наружная несущая стена в бесподвальной части здания)
| | I. ПОСТОЯННО ДЕЙСТВУЮЩИЕ НАГРУЗКИ
|
|
|
|
| |
| Собственный вес стены
| 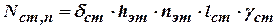
| gn = 0,95
gf = 1
| 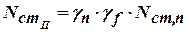
| gn = 0,95
gf = 1,2
| 
| |
| Собственный вес плит перекрытий
и покрытия
| 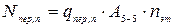
| gn = 0,95
gf = 1
| 
| gn = 0,95
gf = 1,1
| 
| |
| Собственный вес кровли
| 
| gn = 0,95
gf = 1
| 
| gn = 0,95
gf = 1,2
| 
|
Окончание таблицы _____
|
|
|
|
|
|
|
| | II. ВРЕМЕННЫЕ КРАТКОВРЕМЕННО ДЕЙСТВУЮЩИЕ НАГРУЗКИ
|
|
| |
| Полезная нагрузка на перекрытия
| 
| gn = 0,95
gf = 1
y2 = 0,9
| 
| gn = 0,95
gf = 1,2
y2 = 0,9
| 
| |
| Вес людей и материалов в зоне ремонта покрытия
| 
| gn = 0,95
gf = 1
y2 = 0,9
| 
| gn = 0,95
gf = 1,2
y2 = 0,9
| 
| |
| Снеговая нагрузка на покрытие
| 
| gn = 0,95
gf = 1
y2 = 0,9
| 
| gn = 0,95
gf = 1,4
y2 = 0,9
| 
| | ВСЕГО нагрузка на обрез фундамента в сечении 5-5
|  
| 
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Примеры задач для самостоятельного решения. 1.Спрос и предложение на обеды в студенческой столовой описываются уравнениями: QD = 2400 – 100P; QS = 1000 + 250P
1.Спрос и предложение на обеды в студенческой столовой описываются уравнениями: QD = 2400 – 100P; QS = 1000 + 250P...
Дизартрии у детей Выделение клинических форм дизартрии у детей является в большой степени условным, так как у них крайне редко бывают локальные поражения мозга, с которыми связаны четко определенные синдромы двигательных нарушений...
Педагогическая структура процесса социализации Характеризуя социализацию как педагогический процессе, следует рассмотреть ее основные компоненты: цель, содержание, средства, функции субъекта и объекта...
|
Закон Гука при растяжении и сжатии
Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука, по имени установившего этот закон английского физика Роберта Гука в 1678 году...
Характерные черты официально-делового стиля Наиболее характерными чертами официально-делового стиля являются:
• лаконичность...
Этапы и алгоритм решения педагогической задачи Технология решения педагогической задачи, так же как и любая другая педагогическая технология должна соответствовать критериям концептуальности, системности, эффективности и воспроизводимости...
|
|