ИЗВЕСТНОЙ ФОРМЫ
1 Цель работы Исследование оптимальной фильтрации детерминированных сигналов на примере сигнала Баркера, наблюдаемого в присутствии широкополосного гауссовского шума.
2 Основы теории оптимальной фильтрации детермИнированных сигналов в присутствии шума Передача информации в системах электрической связи сопровождается мешающим действием помех, источники которых могут располагаться как вне, так и внутри системы. К помехам, имеющим внешнее происхождение, относятся, например, электромагнитные излучения промышленных установок, транспортных средств, радиолокационных, радионавигационных, радиотелевещательных систем, флуктуационное электромагнитное излучение земной поверхности и небесной сферы. К помехам, возникающим внутри системы, относятся шумы электронных приборов, импульсы, образующиеся при коммутации в линиях связи, отражения сигналов от неоднородностей линии связи. Для выделения сообщений, модулирующих сигнал, необходимо обеспечить его наилучшую наблюдаемость на фоне помех. С этой целью широко используется линейная фильтрация сигнала, т.е. применением линейных электрических фильтров обеспечивается увеличение отношения уровня сигнала к уровню помехи на выходе фильтра по сравнению с подобным отношением на входе. Однако электрический фильтр не только уменьшает уровень помехи, но и искажает форму сигнала. Последнее не является недостатком до тех пор, пока искажение формы не снижает качества выделения сообщения. Электрический фильтр, обеспечивающий наибольшее отношение максимального (пикового) значения сигнала известной формы к эффективному значению шума, называется оптимальным по сформулированному критерию. Впервые подобная задача была решена американским ученым Норсом в 1943 году. Поэтому такой фильтр иногда называют норсовским. Найдем связь характеристик этого фильтра с характеристиками сигнала при его наблюдении в смеси с помехой в виде белого шума со спектральной плотностью мощности, равной N 0/2. Максимальное значение сигнала в момент времени t 0на выходе фильтра с комплексным коэффициентом передачи K (j ω) равно:
где Удельная мощность помехи на выходе фильтра может быть найдена из выражения:
где S п(ω) – спектральная плотность мощности помехи на входе фильтра. В приведенном выражении учтено, что при помехе в виде белого шума S п(ω;) =N 0 /2 отношение пикового значения сигнала к эффективному значению помехи на выходе фильтра определяется выражением:
Применяя к числителю отношения (3) неравенство Коши-Буняковского [3], можно записать:
В последнем выражении равенство достигается при единственном условии:
которое определяет условие оптимальности фильтра по указанному выше критерию. Как видно из (5), абсолютное значение коэффициента передачи такого фильтра пропорционально амплитудному спектру сигнала Таким образом, при помехе с равномерной спектральной плотностью мощности частотные характеристики оптимального фильтра полностью определяются спектральными характеристиками сигнала. Поэтому такой фильтр часто называют согласованным [1]. Найдем отношение пикового значения сигнала к эффективному значению шума на выходе согласованного фильтра. Подставляя (5) в (3), можно получить:
где Отношение пиковой мощности сигнала к средней мощности шума на выходе фильтра в этом случае равно:
где τ;c – длительность сигнала, P c – средняя мощность сигнала на входе фильтра. Импульсная реакция согласованного фильтра может быть записана в виде обратного преобразования Фурье:
Подставляя в приведенное выражение равенство (5), можно получить:
Отсюда следует, что импульсная характеристика согласованного фильтра пропорциональна зеркальному отражению сигнала, сдвинутому на интервал времени t 0. Поскольку процесс на выходе цепи может быть записан в виде свертки входного сигнала с импульсной реакцией этой цепи, то в случае согласованного фильтра выходной процесс пропорционален автокорреляционной функции входного сигнала, сдвинутой на интервал t0 [1,3]:
Как следует из равенства (9), максимум процесса u вых(t) достигается в момент времени t = t 0, и в этот момент времени обеспечиваются наилучшие условия его наблюдения на фоне помех[1]. В случае помехи, не являющейся белым шумом, имеющий спектральную плотность мощности S п(ω),оптимальный фильтр состоит из двух каскадов [3].Первый из них называется «обеляющим» фильтром [3], его задачей является преобразование помехи в белый шум. Квадрат модуля коэффициента передачи «обеляющего» фильтра может быть записан в виде:
где K 1– произвольный коэффициент, определяющий значение уровня спектральной плотности помехи K 12на выходе «обеляющего» фильтра. Вторым каскадом оптимального фильтра является фильтр, согласованный с формой сигнала на выходе «обеляющего» фильтра. Комплексный коэффициент передачи его описывается выражением:
где S C(j ω) – спектральная функция входного сигнала. Структура оптимального фильтра для сигнала, принимаемого в смеси с помехой, имеющей неравномерную спектральную плотность мощности, приведена на рисунке 1.
Рисунок 1 – Структурная схема оптимального фильтра для сигнала, наблюдаемого в смеси с помехой, имеющей неравномерную спектральную плотность мощности Максимальное (пиковое) значение сигнала на выходе фильтра в этом случае равно:
Найдем выражение для мощности помехи на выходе рассматриваемого фильтра:
Учитывая равенства (10) и (11), можно получить:
Находя отношение пиковой мощности сигнала к средней мощности шума на выходе фильтра, получим:
Можно убедиться, что при равномерном спектре помехи S П(ω) = 2 /N 0, равенства (14) и (6) приводят к одинаковому результату. Рассмотрим согласованный фильтр для одиночного видеоимпульса. Выражение для сигнала такой формы имеет вид:
где U 0 – амплитуда импульса, τИ – длительность импульса. Спектральная функция этого сигнала может быть найдена применением преобразования Фурье:
Полагая t 0 = τИ, найдем коэффициент передачи согласованного фильтра:
При выполнении вычислений необходимо иметь в виду, что S C * (j ω) = S C(– j ω). Для нахождения структуры фильтра необходимо учитывать, что комплексный коэффициент передачи K 3(j ω) =
Рисунок 2 – Структурная схема фильтра, согласованного с одиночным видеоимпульсом
Поступающий на вход сигнал разветвляется на два пути – по одному импульс поступает на сумматор, по второму – на цепь задержки, после которой задержанный импульс с противоположным знаком примыкает к не задержанному. В результате интегрирования получившейся последовательности двух разнополярных прямоугольных импульсов процесс u ВЫ Х (t) представляет собой импульс треугольной формы, ширина которого по основанию равна 2τИ. Можно убедиться, что максимум выходного сигнала находится в точке t M = τИ = t 0. Функция автокорреляции сигнала в виде одиночного импульса прямоугольной формы также имеет треугольную форму [2] с максимальным значением в начале координат. Рассмотрим фильтр, согласованный с последовательностью некоторого числа М прямоугольных импульсов одинаковой длины τИ, положительной полярности с заданным значением Т расстояния между ними. Как и в предыдущем случае, найдем спектральную функцию сигнала:
где s 0(t) – одиночный импульс с амплитудой U 0 и длительностью τИ. Используя равенство (16) для спектральной плотности одиночного импульса, линейность и теорему запаздывания – свойства преобразования Фурье [3] – можно получить:
где
множитель, учитывающий повторяемость одиночных импульсов, следующих через интервал Т,
В соответствии со сказанным выше, коэффициент передачи оптимального (согласованного) фильтра для пачки импульсов может быть записан в виде:
где При
В соответствии с равенством (22) реализация фильтра, согласованного с сигналом в виде пачки прямоугольных видеоимпульсов, представляет собой последовательное соединение фильтра, согласованного с одиночным импульсом, и накопителя, являющегося линией задержки с отводами, следующими через интервал Т, соединенной с сумматором задержанных импульсов. Максимум сигнала на выходе фильтра в этом случае достигается в момент времени, соответствующий положению заднего фронта последнего из поступающих на вход фильтра импульсов. Структурная схема и диаграммы процессов в характерных точках согласованного фильтра приведены на рисунке 3, на котором обозначен K 1(j ω) – коэффициент передачи фильтра, согласованного с одиночным импульсом. В настоящей лабораторной работе изучается оптимальная (согласованная) фильтрация последовательности прямоугольных импульсов, называемой семиэлементным сигналом (кодом) Баркера. К подобным сигналам относятся последовательности импульсов переменного знака (фазоманипулированные последовательности), функции корреляции которых имеют локальные экстремумы (максимумы или минимумы), не превышающие относительный уровень 1/ М, где М – число импульсов в последовательности [2]. В настоящее время такие последовательности найдены для М = 3, 4, 5, 7, 11 и 13. Для наиболее интересных случаев
Рисунок 3 – Структурная схема оптимального фильтра для пачки М импульсов и диаграммы напряжений
Таблица 1 Сигналы Баркера
Символом «1» в таблице обозначен импульс положительной полярности, символом «-1» – отрицательной. Амплитуды импульсов должны быть одинаковыми. Выражение для нормированной функции автокорреляции сигнала конечной длительности имеет вид [2]:
где Рассмотрим сигнал Баркера, состоящий из семи вплотную следующих друг за другом прямоугольных импульсов, длительность каждого из которых равна τИ. График функции, описывающий такой сигнал, приведен на рисунке 4.
Рисунок 4 – Семипозиционный сигнал Баркера Выполняя операции, предусмотренные равенством (23), можно убедиться, что нормированная функция автокорреляции такого сигнала имеет вид, представленный на рисунке 5.
Рисунок 5 – Функция автокорреляции семипозиционного сигнала
Согласованный фильтр для сигнала Баркера используемого вида, как и в случае приема пачки импульсов, можно представить в виде последовательного соединения фильтра, согласованного с одиночным импульсом, и накопителя, в котором осуществляется суммирование отдельных импульсов последовательности с учетом их полярности на отдельных позициях. Структурная схема фильтра представлена на рисунке 6.
Рисунок 6 – Структурная схема фильтра, согласованного с семиэлементным кодом Баркера Приведенный на схеме фильтр, согласованный с семиэлементным кодом Баркера, заканчивается входящим в его состав элементарным фильтром с коэффициентом передачи K 1(j ω), являющимся согласованным с одиночным импульсом кода. В ряде случаев для упрощения технической реализации вместо этого фильтра применяется квазиоптимальный, построенный на базе какого-либо типового фильтра. Оптимизация фильтра при этом осуществляется подбором его полосы, обеспечивающим указанное выше максимальное отношение пикового значения сигнала к эффективному значению шума на его выходе, но для заданного, фиксированного вида фильтра. Впервые такую постановку задачи сформулировал советский ученый В.И.Сифоров в 1946г., и решил подобную задачу для фильтра с прямоугольной АЧХ. В лабораторной установке, на которой выполняется данная лабораторная работа, квазиоптимальный фильтр выполнен в виде однозвенной RC -цепи. Как показано в учебнике [З], максимальное отношение пиковой мощности сигнала на выходе фильтра к средней мощности шума достигается при условии
где При выполнении полученного условия отношение пиковой мощности сигнала к средней мощности шума на выходе фильтра составляет 0.814 от максимально возможного, определяемого равенством (7) для импульса прямоугольной формы. Таким образом, ценой упрощения оконечного фильтра в схеме, приведенной на рисунке 6, является двадцатипроцентный проигрыш в энергии сигнала (около 0.9 дБ), что на практике обычно считается допустимым. Необходимо иметь в виду, что замена оптимального фильтра квазиоптимальным обычно оказывается несложной для сигналов сравнительно простой формы. В системах связи чаще всего используются фазоманипулированные сложные сигналы, являющиеся последовательностями радиоимпульсов одной несущей частоты, фазовые сдвиги которых скачкообразно меняются по закону, соответствующему коду импульсной последовательности. Изменения фазы обычно составляет π, т.е. фазы элементарных сигналов меняются на противоположные. Согласованные фильтры для таких сигналов представляют собой сочетание рассмотренных выше многоотводных линий задержки с включенными в необходимых местах инверторами, сумматором и оконечным оптимальным (согласованным) фильтром по отношению к одиночному радиоимпульсу (а не видеоимпульсу, как в предыдущем случае). При этом квазиоптимальный фильтр может быть выполнен в виде колебательного контура с указанным в (24) соотношением постоянной времени и длительности элементарного радиоимпульса. Одним из преимуществ сложных (широкополосных) сигналов по сравнению с «простыми» является возможность повышения разрешающей способности по времени при фиксированной их длительности. Два сигнала называются разрешенными, если можно с высокой вероятностью зафиксировать наличие каждого из них и определить значения их основных параметров. Минимальное расстояние между сигналами, при котором их можно считать разрешенными, называется интервалом разрешения по данному параметру. В данном случае представляет интерес запаздывание по времени одного из сигналов относительно другого, которое может возникнуть, в частности, при многолучевом распространении сигнала в радиосвязи. При отсутствии разрешения возникает интерференция между сигналами, прошедшими по разным путям, в результате которой амплитуда суммарного сигнала может меняться в значительных пределах, что значительно снижает качество приема. При наличии разрешения один из сигналов можно устранить применением временной селекции. Можно также показать, что эффект сжатия сложных сигналов практически устраняет межсимвольные искажения, возникновение которых возможно за счет инерционности канала связи. Таким образом, повышенная разрешающая способность по времени сигналов с фазо-кодовой манипуляцией (к которым относятся сигналы Баркера) является одним из их достоинств, обеспечивающих системам связи, использующим также сигналы, ряд высоких показателей качества. 3 Характеристика лабораторной установки Лабораторная работа «Согласованная фильтрация» выполняется в системе моделирования MATLAB с использованием блоков визуального моделирования Simulink. В составе Simulink-модели функционально сгруппированные блоки формирования сигналов, согласованного фильтра для пачки сигналов и для одиночного сигнала, представленные на рисунке 7.
Рисунок 7 – Упрощенные структуры блока в составе модели «Согласованная фильтрация» Генератор сигнала формирует семипозиционный код Баркера с амплитудным кодированием, форма которого приведена на рисунке 4. Длительность элементарного импульса составляет 2 мкс, длительность сигнала – 14 мкс, техническая ширина его спектра 500 кГц. Сформированный сигнал через ключ «Сигнал» подается на сумматор. Кроме того, на второй вход сумматора может быть подан тот же сигнал с выхода управляемой линии задержки. Величина задержки относительно положения сигнала с выхода генератора может меняться от 2 до 16 мкс. На третий вход сумматора может быть подан шум с внешнего источника через блок «генератор шума». Ширина спектра шума приблизительно равна 500 кГц. Таким образом, на выходной клемме сумматора «Сигнал» можно наблюдать либо любой из трех перечисленных процессов, либо сумму двух из них, либо сумму всех трех. Структурная схема Simulink-модели, соответствующая реальной установке, приведена на рисунке 8.
Рисунок 8 – Блок-схема модели для исследования статистических характеристик согласованной фильтрации, использующей семиэлементный код Баркера
Здесь сигнал, соответствующий семиэлементному коду Баркера, формируется в блоке Group2 (библиотечный блок называется Signal Builder), окно настройки которого показано на рисунке 9. В набор сигналов блока Group2 входят три сигнала:
Рисунок 9 – Окно блока Signal Builder для формирования семиэлементного кода Баркера
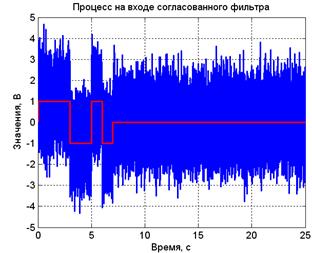
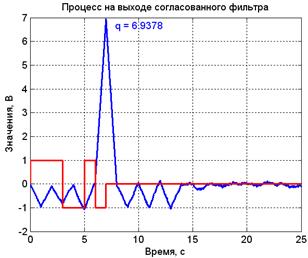
– Barker0 - семиэлементный код Баркера без смещения по оси времени; – Pulse7 - прямоугольный импульс длительностью, одинаковой с первым; – BarkerInv - обращённый семиэлементный код Баркера. В набор сигналов блока Group1 входят два семиэлементных кода Баркера со смещением по оси времени, равным: – длительности одного элемента кода (Barker1); – длительности двух элементов кода (Barker2). Выходы генераторов поодиночке или после суммирования в блоке Add подключаются через аттенюатор (блок GainS) на вход сумматора, куда также через аттенюатор (блок GainN) поступает гауссов белый шум с генератора Random Number. Суммарный (зашумлённый) процесс подаётся на вход набора блоков задержки, умножителей и сумматора, моделирующих обработку в согласованном фильтре. Выход сумматора подключён к фильтру одиночного сигнала (для кода Баркера), состоящего из трёх блоков: линии задержки, вычитающего устройства и интегратора. Индикация результатов моделирования проводится с помощью осциллографа и трёх цифровых дисплеев. Дисплей Var1 показывает текущую дисперсии процесса на входе согласованного фильтра, второй дисплей Var2 – текущую дисперсию на его выходе, а третий – максимальное значение процесса на выходе фильтра за время моделирования. Осциллограф показывает три графика временных зависимостей: самого суммарного процесса, результат обработки на выходе многоотводной линии задержки (межпериодной обработки) и сигнал на выходе фильтра, согласованного с одиночным сигналом кода Баркера. Эти процессы также записываются в рабочее пространство системы MATLAB. Кроме того, с помощью блока simout туда же копируются отсчёты исходного (незашумлённого) сигнала.
4 Подготовка к лабораторной работе В процессе домашней подготовки необходимо выполнить следующие виды работ: 4.1 Изучить теоретические вопросы, связанные с оптимальной фильтрацией детерминированных сигналов, по настоящим указаниям и литературе. 4.2 Построить график функции автокорреляции сигнала Баркера, используемого в лабораторной работе. 4.3 Построить график процесса на выходе фильтра, используемого в лабораторной установке, при наличии на входе суммы сигналов Баркера, сдвинутых на 2 мкс. 4.4 Рассчитать отношение пикового значения сигнала к эффективному значению шума на выходе фильтра, согласованного с семиэлементным сигналом Баркера амплитудой 10-6 В и длительностью 14 мкс, принимаемого в смеси с белым шумом, спектральная плотность мощности которого равна 4.5 Построить график процесса на выходе фильтра, согласованного с семиэлементным кодом Баркера, если на вход поступает прямоугольный видеоимпульс, длительность которого равна длительности сигнала Баркера. Найти пиковое значение сигнала на выходе, если амплитуда сигнала на входе равна одному вольту. 4.6 Построить график процесса на выходе того же фильтра, если на вход поступает сигнал Баркера, следующий в порядке, обратном тому, который формируется генератором лабораторной установки. Найти пиковое значение сигнала на выходе. 4.7 Подготовить ответы на контрольные вопросы.
5 Лабораторное задание 5.1 Составить из блоков пользовательской библиотеки структурную схему модели измерительной установки согласно рисунку 8. Подключить к аттенюатору GainS сигнал семиэлементного кода Баркера Barker0 от блока Group2. Задать коэффициенты усиления GainS и GainN равными 1, что будет соответствовать отношению сигнал/шум для одиночного импульса q 1 = 1.0. Временной интервал моделирования задать равным: Start time = 1e-3 c, Stop time = 25 c, максимальный шаг интегрирования задать равным 1е-3 с. Переключателем Switch2 подсоединить к третьему входу осциллографа идеальный согласованный фильтр одиночного сигнала. 5.2 После прогона модели дважды щёлкнуть по блоку GraphicsShow (запуск М-фунции LabRabRCS7Obr) и провести анализ четырёх графиков временных зависимостей процессов и их автокорреляционных функций. Пояснить надписями соответствующие экспериментальные зависимости и сопоставить их результатами выполнения домашнего задания. 5.3 Провести измерения максимума процесса на выходе идеального согласованного фильтра для одиночного сигнала (блок Maximum), меняя дисперсию шума с помощью аттенюатора GainN в диапазоне от 0 до 35 при шаге 3.5. Рассчитать и построить на бумаге зависимость максимума процесса на выходе фильтра от СКО шума. Сопоставить полученные результаты с отношением сигнал/шум по мощности, вычисленным по установочным параметрам блоков. 5.4 Провести исследование работы квазиоптимального фильтра, подключив к осциллографу переключателем Switch2 выход RC -цепи. Установить дисперсию шума равной 1. Провести измерения максимума процесса на выходе RC -цепи (блок Maximum), меняя постоянную времени цепи 5.5 Подключить к осциллографу переключателем Switch2 выход идеального согласованного фильтра. Подать через блок Add на вход сумматора Sum суммарный сигнал, состоящий из несдвинутого (сигнал Barker0 с блока Group2) и сдвинутого на один импульс (сигнал Barker1 с блока Group1) кода Баркера. При необходимости следует разорвать мешающие связи для соединения нужных блоков. Наблюдать и зафиксировать осциллограммы процессов на выходах аттенюатора, сумматора и согласованного фильтра при отношении сигнал/шум для одиночного импульса q 1 = 1.0. 5.6 Повторить пункт 5.5, подключив к блоку Add вместо сигнала Barker1 сигнал Barker2. Наблюдать и зафиксировать осциллограммы процессов на выходах аттенюатора, сумматора и согласованного фильтра. При необходимости следует разорвать мешающие связи для соединения нужных блоков. Определить время разрешения исходного и задержанного сигналов на входе и выходе согласованного фильтра. 5.7 Наблюдать и зафиксировать процессы на выходе фильтра при подаче на его вход прямоугольного импульса длительностью 5.8 Наблюдать и зафиксировать процессы на выходе фильтра при подаче на его вход прямоугольного импульса длительностью 5.9 Наблюдать и зафиксировать процессы на выходе фильтра, согласованного с прямым сигналом Баркера, при подаче на его вход сигнала в виде обратного кода Баркера (сигнал BarkerInv с блока Group1). Для этого установить снова длительность задержки фильтра одиночного сигнала 1 с (блок Delay), его вход с помощью переключателя Switch1 подключить к выходу сумматора линии задержки Sum of Elements. При необходимости следует разорвать мешающие связи для соединения нужных блоков. Измерить максимальное значение отклика при отношении сигнал/шум q 1 = 1 и сравнить его с расчетным, полученным при домашней подготовке в соответствии с п.п. 4.6. 5.10Наблюдать и зафиксировать процессы на выходе фильтра, согласованного с обратным сигналом Баркера, при подаче на его вход сигнала в виде обратного кода Баркера (сигнал BarkerInv с блока Group1). Для этого установить 7 весовых коэффициентов фильтра (блоки Gain0 – Gain6) в согласно обратному коду Баркера. Измерить максимальное значение отклика и сравнить его с полученным при домашней подготовке в соответствии с п.п. 4.6. 6 Требования к отчету Отчет должен содержать: 6.1 Формулировка целей лабораторной работы. 6.2 Функциональная схема установки с подключенными внешними приборами. 6.3 Результаты домашней подготовки (расчеты и графики 6.4 Блок-схема Simulink-модели. 6.5 Результаты лабораторных экспериментов (рисунок 10) с поясняющими надписями. 6.6 Выводы по результатам подготовки и экспериментальных исследований. При формулировке выводов обратить внимание на соответствие результатов экспериментов теоретическим положениям, приведенным в разделе 2, и результатам расчетов при домашней подготовке.
Рисунок 10 – Пример графиков временных процессов при моделировании семиэлементного кода Баркера
7 Контрольные вопросы 7.1 Какой фильтр называется оптимальным при наблюдении детерминированного сигнала в присутствии шума с постоянной спектральной плотностью мощности. Что такое согласованный фильтр? 7.2 Как зависит коэффициент передачи согласованного фильтра от спектральной функции сигнала? 7.3 Как связана импульсная реакция согласованного фильтра с формой входного сигнала? 7.4 Как связан отклик от действия сигнала на выходе согласованного фильтра с функцией автокорреляции сигнала? 7.5 От чего зависит отношение максимального значения сигнала к эффективному значению шума на выходе согласованного фильтра? 7.6 Как найти коэффициент передачи оптимального фильтра, если шум на его входе не является «белым»? 7.7 Почему согласованный фильтр называется оптимальным? 7.8 Изобразите структурную схему фильтра, согласованного с одиночным прямоугольным импульсом? Какую форму имеет сигнал на выходе этого фильтра? 7.9 Как формируется согласованный фильтр при наблюдении пачки импульсов одинаковой формы? 7.10 Что такое гребенчатый фильтр? 7.11 Какое главное свойство имеют сигналы Баркера? 7.12 Какой из сигналов Баркера является наилучшим? 7.13 Сколько различных сигналов Баркера можно создать на базе последовательности с фиксированным числом импульсов (например, с числом импульсов 11)? 7.14 Изобразите структурную схему оптимального фильтра для сигнала Баркера. 7.15 Чем отличается оптимальный фильтр для последовательности радиоимпульсов от оптимального фильтра для последовательности видеоимпульсов? Показать на примере фильтра для кода Баркера. 7.16 Доказать, что циклическая перестановка импульсов в коде Баркера не дает новых кодов, обладающих свойствами кодов Баркера.
|

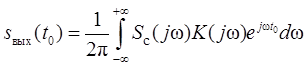 , (1)
, (1)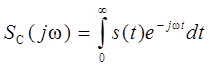 – спектральная функция сигнала s (t)на входе фильтра.
– спектральная функция сигнала s (t)на входе фильтра. , (2)
, (2) . (3)
. (3) . (4)
. (4) , (5)
, (5) , а фазочастотная характеристика содержит два слагаемых, первое из которых равно по абсолютному значению, но противоположно по знаку фазовому спектру сигнала, второе слагаемое определяет временное положение максимума отклика. Для физически реализуемого фильтра необходимо выполнение условия
, а фазочастотная характеристика содержит два слагаемых, первое из которых равно по абсолютному значению, но противоположно по знаку фазовому спектру сигнала, второе слагаемое определяет временное положение максимума отклика. Для физически реализуемого фильтра необходимо выполнение условия  , где
, где  – длительность сигнала на входе фильтра.
– длительность сигнала на входе фильтра. , (6)
, (6) – удельная энергия сигнала, т.е. энергия, которая рассеивается на сопротивлении 1 Ом.
– удельная энергия сигнала, т.е. энергия, которая рассеивается на сопротивлении 1 Ом. , (7)
, (7) .
. . (8)
. (8) . (9)
. (9) (10)
(10) (11)
(11)
 . (12)
. (12) .
. . (13)
. (13)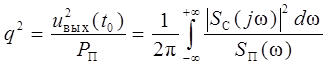 . (14)
. (14)
 (15)
(15)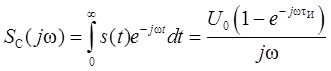 . (16)
. (16) . (17)
. (17) имеет цепь, осуществляющую запаздывание входного сигнала на длительность импульса τИ, а
имеет цепь, осуществляющую запаздывание входного сигнала на длительность импульса τИ, а  имеет интегратор. Тогда структура фильтра, согласованного с одиночным видеоимпульсом, может быть представлена в виде, изображенном на рисунке 2.
имеет интегратор. Тогда структура фильтра, согласованного с одиночным видеоимпульсом, может быть представлена в виде, изображенном на рисунке 2.
 , (18)
, (18) , (19)
, (19) (20)
(20) – спектральная плотность одиночного импульса амплитудой U 0 и длительностью τИ.
– спектральная плотность одиночного импульса амплитудой U 0 и длительностью τИ. (21)
(21) – момент времени, в котором напряжение сигнала на выходе фильтра достигает максимума.
– момент времени, в котором напряжение сигнала на выходе фильтра достигает максимума.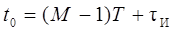 коэффициент передачи согласованного фильтра с точностью до постоянного множителя совпадает с выражением для спектральной плотности сигнала:
коэффициент передачи согласованного фильтра с точностью до постоянного множителя совпадает с выражением для спектральной плотности сигнала: . (22)
. (22) коды Баркера имеют вид, приведенный в таблице 1.
коды Баркера имеют вид, приведенный в таблице 1.

 (23)
(23) – удельная энергия сигнала.
– удельная энергия сигнала.


 (24)
(24) – постоянная времени RC -фильтра.
– постоянная времени RC -фильтра.


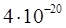 Дж.
Дж. от 0.2 с до 2 с при шаге 0.2 с. Построить на бумаге зависимость максимума процесса на выходе фильтра от постоянной времени цепи
от 0.2 с до 2 с при шаге 0.2 с. Построить на бумаге зависимость максимума процесса на выходе фильтра от постоянной времени цепи  . Сопоставить полученные результаты с теоретическими положениями.
. Сопоставить полученные результаты с теоретическими положениями. (сигнал Pulse7 с блока Group1). При необходимости следует разорвать мешающие связи для соединения нужных блоков. Измерить максимальное значение отклика и сравнить его с расчетным, полученным при домашней подготовке (пункт 4.5). Отношение сигнал/шум для одиночного импульса оставить равным q 1 = 1.0.
(сигнал Pulse7 с блока Group1). При необходимости следует разорвать мешающие связи для соединения нужных блоков. Измерить максимальное значение отклика и сравнить его с расчетным, полученным при домашней подготовке (пункт 4.5). Отношение сигнал/шум для одиночного импульса оставить равным q 1 = 1.0. (сигнал Pulse7 с блока Group1) при согласовании фильтра с этим сигналом. Для этого с помощью переключателя Switch1 подключить выход сумматора Sum напрямую к входу блока Delay согласованного фильтра. Величину задержки в блоке Delay установить также равной 7 с, а q 1 = 1.0. Измерить максимальное значение отклика и сравнить его с расчетным, полученным при домашней подготовке (пункт 4.5).
(сигнал Pulse7 с блока Group1) при согласовании фильтра с этим сигналом. Для этого с помощью переключателя Switch1 подключить выход сумматора Sum напрямую к входу блока Delay согласованного фильтра. Величину задержки в блоке Delay установить также равной 7 с, а q 1 = 1.0. Измерить максимальное значение отклика и сравнить его с расчетным, полученным при домашней подготовке (пункт 4.5).