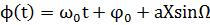Модуляция

 

Сигналы формируются путем изменения тех или иных параметров физического носителя в соответствии с передаваемым сообщением. Этот процесс (изменения параметров носителя) принято называть модуляцией.

Общий принцип модуляции состоит в изменении одного или нескольких параметров несущего колебания (переносчика) f(t,α,β, …) в соответствии с передаваемым сообщением. Так если в качестве переносчика выбрано гармоническое колебание f(t)=Ucos(ω₀t+φ), то можно образовать три вида модуляции: амплитудную (АМ), частотную (ЧМ) и фазовую (ФМ).

 

 

Рисунок 1.4 – Формы сигналов при двоичном коде для различных видов дискретной модуляции

 

Амплитудная модуляция состоит в пропорциональном первичному сигналу x(t) изменении амплитуды переносчика U_AM=U₀+ax(t). В простейшем случае гармонического сигнала x(t)=XcosΩt амплитуда равна:

 

(1.10)

 

В результате имеем АМ колебание:

 

(1.11)

 

 

Рисунок 1.5 – Графики колебаний x(t), u и u_AM

 

Рисунок 1.6 – Спектр АМ колебания

 

На рисунке 1.5 изображены графики колебаний x(t), u и u_AM. Максимальное отклонение амплитуды U_AM от U₀ представляет амплитуду огибающей U_Ω=aX. Отношение амплитуды огибающей к амплитуде несущего (немодулированного) колебания:

 

(1.12)

 

m – называется коэффициентом модуляции. Обычно m<1. Коэффициент модуляции, выраженный в процентах, т.е. (m=100%) называют глубиной модуляции. Коэффициент модуляции пропорционален амплитуде модулирующего сигнала.

Используя выражения (1.12), выражение (1.11) записывают в виде:

 

(1.13)

 

Для определения спектра АМ колебания раскроем скобки в выражении(1.13):

 

(1.14)

 

Согласно (1.14) АМ колебание является суммой трех высокочастотных гармонических колебаний близких частот (поскольку Ω<<ω₀ или F<<f₀):

- колебания несущей частоты f₀ с амплитудой U₀;

- колебания верхней боковой частоты f₀+F;

- колебания нижней боковой частоты f₀-F.

Спектр АМ колебания (1.14) приведен на рисунке 1.6. Ширина спектра равна удвоенной частоте модуляции: ∆f_AM=2F. Амплитуда несущего колебания при модуляции не изменяется; амплитуды колебании боковых частот (верхней и нижней) пропорциональны глубины модуляции, т.е. амплитуде X модулирующего сигнала. При m=1 амплитуды колебаний боковых частот достигают половины несущей (0,5U₀).

Несущее колебание никакой информации не содержит, и в процессе модуляции оно не меняется. Поэтому можно ограничиться передачей только боковых полос, что и реализуется в системах связи на двух боковых полосах (ДБП) без несущей. Больше того, поскольку каждая боковая полоса содержит полную информацию о первичном сигнале, можно обойтись передачей только одной боковой полосы (ОБП). Модуляция, в результате которой получаются колебания одной боковой полосы, называется однополосной (ОМ).

Очевидными достоинствами систем связи ДБП и ОБП являются возможности использования мощности передатчика на передачу только боковых полос (двух или одной) сигнала, что позволяет повысить дальность и надежность связи. При однополосной модуляции, кроме того, вдвое уменьшается ширина спектра модулированного колебания, что позволяет соответственно увеличить число сигналов, передаваемых по линии связи в заданной полосе частот.

Фазовая модуляция заключается в пропорциональном первичному сигналу x(t) изменении фазы φ переносчика u=U₀cos(ω₀t+φ).

 

(1.15)

 

где a – коэффициент пропорциональности.

Амплитуда колебания при фазовой модуляции не изменяется, поэтому аналитическое выражение ФМ колебания

 

(1.16)

 

Если модуляция осуществляется гармоническим сигналом x(t)=XsinΩt, то мгновенная фаза

 

(1.17)

 

Первые два слагаемых (1.17) определяют фазу немодулированного колебания, третье – изменение фазы колебания в результате модуляции.

Фазомодулированное колебание наглядно характеризуется векторной диаграммой рисунок 1.7, построенной на плоскости, вращающейся по часовой стрелке угловой частотой ω₀. Немодулированному колебанию соответствует подвижный вектор U₀. Фазовая модуляция заключается в периодическом изменении с частотой Ω повороте вектора U относительно U₀ на угол ∆φ(t)=aXsinΩt. Крайние положения вектора U обозначены U^’ и U^’’. Максимальное отклонение фазы модулированного колебания от фазы немодулированного колебания:

 

(1.18)

 

где M – индекс модуляции. Индекс модуляции М пропорционален амплитуде Х модулирующего сигнала.

 

 

Рисунок 1.7 – Векторная диаграмма фазомодулированного колебания

 

Используя (1.18), перепишем ФМ колебание (1.16) как

 

u=U0cos(ω0t+φ0+MsinΩt)

(1.19)

 

Мгновенная частота ФМ колебания

 

ω=U(ω0+MΩcosΩt)	(1.20)

Таким образом, ФМ колебание в разные моменты времени имеет различные мгновенные частоты, отличающиеся от частоты несущего колебания ω₀ на величину ∆ω= MΩcosΩt, что позволяет рассматривать ФМ колебание как модулированное по частоте.

Частотная модуляция заключается в пропорциональном изменении первичному сигнала x(t) мгновенной частоты переносчика:

 

ω=ω0+ax(t)

(1.21)

 

где a – коэффициент пропорциональности.

Мгновенная фаза ЧМ колебания

 

(1.22)

 

 

Аналитическое выражение ЧМ колебания с учетом постоянства амплитуды можно записать в виде:

 

(1.23)

 

Девиация частоты – максимальное ее отклонение от несущей частоты ω_0, вызванное модуляцией:

 

∆ωA=aX

(1.24)

 

Аналитическое выражение этого ЧМ колебания:

 

(1.25)

 

Слагаемое (∆ω_Д/Ω)sinΩt характеризует изменение фазы, получающееся при ЧМ. Это позволяет рассматривать ЧМ колебание, как ФМ колебание с индексом модуляции

 

(1.26)

 

и записать его аналогично:

 

(1.27)

 

Из сказанного следует, что ФМ и ЧМ колебания имеют много общего. Так колебание вида (1.27) может быть результатом как ФМ, так и ЧМ гармоническим первичным сигналом. Кроме того, ФМ и ЧМ характеризуются одними и теми же параметрами (индексом модуляции М и девиацией частоты ∆f_Д), связанными между собой одинаковыми соотношениями: (1.21) и (1.24).

Наряду с отмеченным сходством частотной и фазовой модуляции между ними имеется и существенное отличие, связанное с различным характером зависимости величин М и ∆f_Д от частоты F первичного сигнала:

- при ФМ индекс модуляции не зависит от частоты F, а девиация частоты пропорциональна F;

- при ЧМ девиация частоты не зависит от частоты F, а индекс модуляции обратно пропорционален F.