Зачем нужна выборка

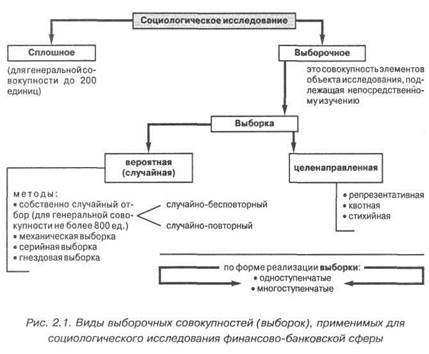
Правильная выборка — залог успеха и необходимая предпосыл­ка любого опроса, если это не общенациональная перепись насе­ления. Если социолог неправильно составил выборочную совокуп­ность, т.е. группу людей, которую собирается опросить, резуль­таты исследования окажутся неверными, а потому и никому не нужными.

Почему нерационально и практически невозможно опрашивать всех людей, составляющих объект исследования?

Можно приблизительно рассчитать, во что обойдется сплош­ной опрос взрослых жителей хотя бы одного городского района с численностью населения, скажем, 200 тыс. чел. Учитывая, что один анкетер (интервьюер) в состоянии опросить не более трех человек в час, при семичасовом рабочем дне его выработка соста- 84

ящих президентских выборах для них предпочтительнее. В тече­ние ряда лет результаты опроса, проводившегося журналом, ока­зывались настолько точными, что опрос, проведенный в сентяб­ре, казалось, делал ноябрьские выборы малосущественными. Да и как при такой большой выборке могла произойти ошибка? Од­нако в 1936 г. именно это и случилось: с большим перевесом го­лосов (60:40) победа была предсказана кандидату от республикан­ской партии Альфу Ландону. Однако когда выборы состоялись, он потерпел сокрушительное поражение. Иначе говоря, Ландон про­играл Франклину Д. Рузвельту практически с тем же результатом, с которым должен был победить. Доверие читателей к «Литэрари дайджест» было серьезно подорвано, вскоре журнал перестал вы­ходить. Такой оказалась цена методической ошибки.

Что же произошло? Все очень просто: в голосовании, прове­денном «Дайджест», использовалась смещенная выборка. Почто­вые открытки рассылались людям, чьи имена были извлечены из двух источников: телефонных справочников и списков регист­рации автомобилей. И хотя прежде этот метод отбора не слиш­ком отличался от других методов, совсем по-другому обстояло дело теперь, после Великой депрессии в 1936 г., когда менее со­стоятельные избиратели, наиболее вероятная опора Рузвельта, не могли позволить себе иметь телефон, не говоря уж об автомоби­ле. Таким образом, выборка, использовавшаяся в опросе, орга­низованном «Дайджест», была смещена в сторону тех, кто, ско­рее всего, должен был выступать за республиканцев, и при этом еще удивительно, что у Рузвельта оказался такой хороший ре­зультат.

Выборочный метод имеет очевидные преимущества перед сплошным изучением генеральной совокупности, так как сокра­щает объем работы (за счет уменьшения числа наблюдений), по­зволяет экономить силы и средства, получать информацию о та­ких совокупностях, полное обследование которых практически невозможно или нецелесообразно. Но происходит все это лишь в том случае, если соблюдаются научные правила выборочного исследования.

Опыт показал, что правильно произведенная выборка доволь­но хорошо представляет или репрезентирует (от лат. represento — представляю) структуру и состояние генеральной совокупности. Однако полного совпадения выборочных данных с данными об­работки генеральной совокупности, как правило, не бывает. В этом и заключается недостаток выборочного метода, на фоне ко­торого видны преимущества сплошного описания генеральной совокупности.

Ввиду неполного отображения выборкой статистических харак­теристик (параметров) генеральной совокупности перед исследо­вателем возникает важная задача: во-первых, учитывать и соблю­дать те условия, при которых выборка наилучшим образом реп­резентирует генеральную совокупность, а во-вторых, в каждом конкретном случае устанавливать, с какой уверенностью можно перенести результаты выборочного наблюдения на всю генераль­ную совокупность, из которой выборка взята.

Репрезентативность выборки зависит от целого ряда условий, и прежде всего от того, как она осуществляется — или планомер­но (т.е. по заранее намеченной схеме), или путем непланомерно­го отбора элементов из генеральной совокупности. В любом слу­чае выборка должна быть типичной и вполне объективной. Эти требования должны выполняться неукоснительно как наиболее существенные условия репрезентативности выборки. Прежде чем обрабатывать выборочный материал, его нужно тщательно прове­рить и освободить выборку от всего лишнего, что нарушает усло­вия репрезентативности. В то же время при образовании выбор­ки нельзя поступать по произволу, включать в ее состав только те варианты, которые кажутся типичными, а все остальные брако­вать. Доброкачественная выборка должна быть объективной, т.е. производиться без предвзятых побуждений, при исключении субъективных влияний на ее состав. Выполнению этого условия репрезентативности отвечает принцип рандомизации (от англ. randomization), или случайного отбора элементов из генеральной совокупности. Этот принцип положен в основу теории выбороч­ного метода и должен соблюдаться во всех случаях образования репрезентативной выборочной совокупности, не исключая и слу­чаев планомерного или преднамеренного отбора.

2.2. Основные понятия и сущность выборочного метода

При построении социологической выборки используется мно­жество специальных терминов, в том числе два важнейших — ге­неральная и выборочная совокупности.

Совокупность, из которой отбираются варианты для совмест­ного изучения, называется генеральной, а отобранная из генераль­ной совокупности часть ее членов носит название выборки, или выборочной совокупности. Объем генеральной совокупности обо­значается символом N, а объем выборочной совокупности — п. Обычно эти символы размещают в заголовке таблице, которая

получилась у социолога после анализа данных, либо в подлежа­щем³ таблицы.

Генеральной совокупностью считают все население или ту его часть, которую социолог намерен изучить, совокупность людей, обладающих одним или несколькими свойствами, подлежащими изучению. Часто генеральная совокупность (еще называемая по­пуляцией) настолько крупная, что опрос каждого представителя чрезвычайно обременителен и дорогостоящ. Это те, на кого на­правлен теоретический интерес социолога (в том смысле, что уз­нать о каждом представителе генеральной совокупности ученый может только косвенно — на основе информации о выборочной совокупности).

В англоязычной литературе дословного аналога термину «реп­резентативность» не существует. Вместо него используется другой — «популяция» (population), который, как и русское слово «генераль­ная совокупность», имеет два значения. Первое — генеральная со­вокупность, т.е. все люди, на которых мы хотим распространить полученные в своем исследовании выводы и на которых направ­лен наш теоретический интерес. В англоязычных источниках так и пишут: «population of interest»⁴.

Второе значение — список людей, на основании которого со­ставляется позже выборочная совокупность. Их называют едини­цами наблюдения. Они считаются элементами генеральной сово­купности. Список единиц наблюдения, который нумеруется с использованием таблицы случайных чисел, в отечественной ли­тературе специального названия не имеет, как не имеет он тако­вого и в англоязычной социологии.

Выборкой называется совокупность элементов объекта социо­логического исследования, подлежащая непосредственному изу­чению. Понятие выборки в статистике и социологии рассматри­вается в двух значениях.

♦ Выборка (как результат действия) — представительная часть генеральной совокупности, в которой закон распределения при­знака соответствует закону распределения этого признака в гене­ральной совокупности.

♦ Выборка (как способ или процесс действия) — способ отбора объектов генеральной совокупности в выборочную.

Выборка должна наилучшим образом репрезентировать объект исследования (генеральную совокупность).

Выборочная совокупность — уменьшенная модель генеральной совокупности. Иначе говоря, это множество людей, которых со­циолог опрашивает. В выборку, или выборочную совокупность, входят только те, кого социолог намеревается непосредственно оп­росить. Представим, что предметом его исследования, т.е. темой, выступает экономическая активность пенсионеров. Все пенсионе­ры — пожилые люди в возрасте старше 55 (женщины) и 60 (муж­чины) лет — будут составлять генеральную совокупность. По спе­циальным формулам социолог рассчитал, что ему достаточно опросить 2,5 тыс. пенсионеров. Это и станет его выборочной со­вокупностью.

Основное правило ее составления гласит: каждый элемент ге­неральной совокупности должен иметь одинаковые шансы попасть в выборку. Но как этого добиться? Прежде всего надо узнать как можно больше свойств, или параметров генеральной совокупно­сти, например разброс в возрасте, доходах, национальности, мес­тах проживания респондентов. Разброс в возрасте респондентов называется вариацией, конкретные величины возраста — значени­ями, а совокупность всех значений образует переменную.

Таким образом, переменная «возраст» имеет значения от 0 до 70 (средняя продолжительность жизни) и более лет. Значения группируются в интервалы: 0—5, 6—10, 11—15 лет и т.д. Их мож­но группировать иначе, все зависит от задач исследования. Ин­тервалы значений переменной «возраст» в случае с пенсионерами начинаются с 55 и 60 лет.

Все население, целая нация или очень большая социальная группа редко выступают генеральной совокупностью. В большин­стве эмпирических исследований социолога интересует частная проблема, например рост числа разводов среди молодых семей в крупных городах или интерес к инвестиционной деятельности среди представителей среднего класса столичного города. Разво­ды и инвестиционная деятельность — это те темы, которые инте­ресуют конкретного исследователя в данный период времени. Соответственно все люди, втянутые в этот процесс или участву­ющие в данном событии, будут называться группой интереса⁵. Их могут быть тысячи или десятки тысяч человек. Они составляют исходную популяцию или генеральную совокупность, из которой социолог строит выборочную совокупность и опрашивает ее.

Итак, совокупность людей, на которую вы распространяете свои выводы, называется генеральной совокупностью, популяци-

ей, группой интереса (такое название происходит от направлен­ности теоретического интереса ученого).

Кого именно относить к генеральной совокупности, определя­ют цели исследования, а кого включать в выборочную совокуп­ность, решают математические методы. Если социолог намерева­ется взглянуть на Афганскую войну глазами ее участников, в ге­неральную совокупность войдут все воины-афганцы, но опрашивать придется небольшую часть — выборочную совокуп­ность. Для того чтобы выборка точно отражала генеральную со­вокупность, социолог придерживается правила: любой воин-аф­ганец, независимо от места жительства, места работы, состояния здоровья и других обстоятельств, возможно, затрудняющих его поиск, должен иметь одинаковую вероятность попасть в выбороч­ную совокупность.

Сущность выборочного метода заключается в том, чтобы по свойствам части (выборки) судить о численных характеристиках целого (генеральной совокупности), по отдельным группам эле­ментов — об их общей совокупности, которая иногда мыслится как совокупность неограниченно большого объема. Основу выбороч­ного метода составляет та внутренняя связь, которая существует в популяциях между единичным и общим, частью и целым.

Репрезентативной выборкой в социологии считается такая вы­борочная совокупность, основные характеристики которой полно­стью совпадают (представлены в той же пропорции или с той же частотой) с такими же характеристиками генеральной совокупно­сти. Только для этого типа выборки результаты обследования час­ти единиц (объектов) можно распространять на всю генеральную совокупность. Необходимое условие для построения репрезентатив- ной выборки — наличие информации о генеральной совокупности, т.е. либо полный список единиц (субъектов) генеральной совокупности, либо информация о структуре по характеристикам, существенно влияющим на отношение к предмету исследования.

Под репрезентативностью в социологии понимают такие свой-ства выборки, которые позволяют ей выступать на момент опро- са моделью, представителем⁶ генеральной совокупности. Иными словами, репрезентативная выборка представляет собой микро-косм, меньшую по размеру, но точную модель генеральной сово-купности, которую она должна отражать (по значимым для иссле-дования параметрам). В той степени, в какой выборка является репрезентативной, выводы, основанные на изучении этой выбор-

ки, можно без всяких опасений считать применимыми к исход­ной совокупности. Такое распространение результатов в зарубеж­ной литературе называют генерализуемостью⁷.

Репрезентативным считается такое исследование, при котором отклонение в выборочной совокупности по контрольным призна­кам не превышает 5%. Практика работы социологов позволяет с достаточной надежностью проводить репрезентативные опросы, руководствуясь элементарными правилами. При пилотажном оп­росе небольшой генеральной совокупности (например, в рамках факультета численностью до 100—250 чел.) репрезентативным бу­дет сплошное анкетирование. В масштабах вуза достаточно будет опросить 25% от общего числа студентов.

Как только социолог определился с тем, кого он хочет опро­сить, он определил основу выборки. После чего решается вопрос о типе выборки.

Типами выборки называются основные разновидности статисти­ческой выборки: случайная (вероятностная) и неслучайная (неве­роятностная). Вместо термина «тип выборки» часто употребляют слова «вид» и «разновидность», что также правильно. Тип выборки говорит о том, как люди попадают в выборочную совокупность, объем выборки сообщает о том, какое их количество туда попало.

Методом выборки будем называть способ построения того типа выборки, название которого этот метод носит, например метод вероятностной выборки. В социологии методом называют основ­ной способ сбора, обработки или анализа данных; правила и про­цедуры, с помощью которых устанавливается связь между факта­ми, гипотезами и теориями.

Для каждого типа выборки разработаны свои математические аппараты и процедуры. Так, в простой случайной выборке все элементы из списка людей, составляющих основу выборки, про­нумеровываются и с помощью таблицы случайных чисел из них отбирается искомая совокупность.

Для обеспечения репрезентативности требуется полный и точ­ный перечень единиц выборочной совокупности. Этот перечень образует основу выборки. Элементы, предназначенные для отбора, называются единицами отбора. Элемент генеральной совокупно­сти, с которого непосредственно ведется сбор информации, на­зывается единицей наблюдения. Обычно единица наблюдения — это отдельный человек. Отбор из списка лучше всего производить, нумеруя единицы и используя таблицу случайных чисел, хотя ча-

сто применяется квазислучайный метод, когда из перечня просто­го берется каждый w-й элемент.

Если основа выборки включает список единиц отбора, то структура выборки подразумевает их группировку, отражающую процентное распределение генеральной совокупности по каким-то важным признакам, например распределение индивидов по профессии, квалификации, полу или возрасту.

Структура выборки— процентные пропорции признаков объекта, на основании которых составляется выборочная совокуп­ность.

Если в генеральной совокупности, например, 30% молодежи, 50% людей среднего возраста и 20% пожилых, то и в выборочной совокупности должны соблюдаться те же самые процентные про­порции трех возрастов. К возрастам могут добавиться классы, пол, национальности и т.д. Для каждого признака устанавливаются процентные пропорции в генеральной и выборочной совокупно­стях. Расхождение структуры двух совокупностей ведет к ошибке репрезентативности. Таким образом, структура выборки — процент­ные пропорции признаков объекта, на основании которых состав­ляется выборочная совокупность.

Если тип выборки говорит о том, как попадают люди в выбо­рочную совокупность, то объем выборки сообщает о том, какое их количество попало сюда.

В программе эмпирического исследования тщательно описыва­ется проект выборки, который в последующем может уточняться. В проекте выборки указываются принципы выделения из объекта той совокупности людей (либо иных источников информации), которые впоследствии будут охвачены опросом; обосновывается техника проведения опроса; указываются подходы к определению достоверности полученной информации (это необходимо для того, чтобы удостовериться в степени правомерности распространения полученных выводов на весь объект исследования).

Составление выборки — процесс выбора единиц (людей, орга­низаций и т.п.) из интересующей социолога генеральной совокуп­ности с таким условием, чтобы, проведя свое исследование, уче­ный мог обобщить полученные результаты снова на всю генераль­ную совокупность, из которой осуществлялась выборка.

Составление выборки — очень сложная процедура, включаю­щая множество действий и этапов, на каждом из которых социо­лог может допустить ошибку. Ранняя ошибка порождает после­дующие, нарастает снежный ком искаженной информации, кото­рый способен парализовать исследование или свести его ценность к нулю. Цепочка ошибок, сделанных самим ученым, либо одна из

них называется систематической ошибкой. Например, даже если вы четко определились с генеральной совокупностью, очень слож­но установить, сколько именно человек ее составляют. Или пред­положим, социолог установил общую численность генеральной совокупности, но он никак не может составить список лиц, пред­ставляющих собой основу выборочной совокупности. Если и эта трудность устранена, возникает новая: из списка подлежащих оп­росу лиц далеко не все доступны опросу. Если все респонденты готовы подвергнуться испытанию, то и в этом случае никто не даст гарантии, что они в последний момент не откажутся, дадут истин­ные сведения, что на их мнение никто не повлияет и т.п. Таким образом, социологический опрос превращается в рисковый биз­нес, где ученого подстерегает множество трудностей, неожидан­ностей и неприятностей. И все надо уметь преодолевать.

Высшей пробой профессионально выполненной работы служит то обстоятельство, что социолог из одной и той же генеральной совокупности может сделать две или три выборки, которые, бу­дучи разными по составу респондентов, дают одинаковые стати­стические распределения ответов. Если в первой выборке от 60 до 70% респондентов не удовлетворены трудом, то и в трех других процент неудовлетворенных должен быть таким же. Если это так, то вы сделали правильную выборку.

В практике эмпирических исследований широко употребляет­ся понятие целевой выборки. Целевые выборки — группы физичес­ких или юридических лиц, отвечающие одному или нескольким определенным критериям, устанавливаемым ученым при органи­зации исследования. Респонденты в целевую группу отбираются на основании фильтрующих вопросов, которые и позволяют оп­ределить соответствие этим критериям. Например, при исследо­ваниях среди населения критерием отбора в целевую выборку может являться уровень доходов свыше 5 тыс. руб., использова­ние компьютера не реже трех раз в неделю, наличие дома быто­вой техники определенной марки. Критерии отбора зависят от задач исследования.

Выборка в количественном и качественном исследованиях стро­ится на противоположных принципах. В первом случае она явля­ется статистической и основана на поиске гомогенной группы респондентов, совпадающих по главным признакам (например, возраст, пол, класс). Во втором случае стремятся найти непохо­жих людей, сделать группу респондентов гетерогенной; выбор нового респондента, объекта или ситуации происходит по прин­ципу их противоположности и вариативности. Избегая однород­ности (гомогенности) выборочной совокупности, ученые таким 92

способом стараются отразить как можно больше аспектов изучае­мого явления, осветить его с разных сторон, добиваясь комплек­сного и всестороннего изучения. Выборка в качественном иссле­довании называется теоретической.

Численность выборочной совокупности варьируется здесь в диапазоне от 20 до 50 единиц. Строгих количественных парамет­ров не существует — они зависят от задач исследования. Правда, негласно социологи используют определенный верхний предел — порог насыщения, который достигается, когда каждое последую­щее интервью не привносит в изучаемое явление никакого раз­нообразия, но лишь повторяет данные предыдущих интервью.

Это не только порог насыщения, но и точка расхождения двух стратегий. Представители количественной методологии радуют­ся тому моменту, когда каждое последующее интервью начинает повторять предыдущее. С этой точки открываются захватывающие перспективы, как вид из окна, — социолог предчувствует появле­ние тенденции, а возможно, и статистической закономерности. А вот его сопернику тенденции и статистика не нужны. Он ищет несхожесть, разнообразие, неповторяемость.

2.3. Типы и методы выборки

К сожалению, в социологической литературе, причем не толь­ко в отечественной, но и в зарубежной, не наведен порядок в от­ношении четкой классификации типов выборки и методов ее по­лучения. Можно встретить самые разные названия для одного и того же типа выборки. Нет единого взгляда на то, как разделяются выборки на главные и второстепенные типы, что куда относится. Кратко охарактеризуем точку зрения группы известных социологов.

В ставшей уже классическим учебником книге «Социологичес­кое исследование» В.А. Ядов не дает четкой схемы распределения типов выборки по группам и видам. Однако из контекста ясно, что автор выделяет: 1) репрезентативную статистическую выбор­ку и 2) целевую аналитическую выборку⁸. При небольших по чис­ленности генеральных совокупностях применяют одну из разно­видностей первого типа — случайную бесповторную выборку, при больших генеральных совокупностях используют многоступенча­тый отбор по районам.

Г.Г. Соколова⁹ различает следующие способы формирования выборочной совокупности: а) метод типичных отдельных случа­ев, называемый также монографическим; б) статистические вы­борочные методы. Последние можно разделить на две основные группы: выбор по усмотрению (неслучайный) и случайный (ве­роятностный) выбор. Выбор по усмотрению подразделяется на целенаправленный и выбор по квотам. Квотная выборка строит­ся как модель, воспроизводящая структуру генеральной совокуп­ности в виде квот (пропорций) распределения изучаемых призна­ков. При целенаправленной выборке из генеральной совокупно­сти выбираются типичные элементы с тем, чтобы таким образом получить уменьшенную модель генеральной совокупности. Слу­чайный (вероятностный) выбор подразделяется на: чисто случай­ный, выбор слоями (районирование), выбор гнездами (серийный).

Н.Н. Чурилов предлагает типологию выборки, которую с не­которыми оговорками можно считать наиболее распространенной в отечественной социологии или, скажем так, популярной. К слу­чайным выборкам он относит: 1) вероятностную, 2) систематичес­кую, 3) районированную (стратифицированную), 4) гнездовую, а к неслучайным — 1) «стихийную», 2) квотную, 3) метод «основ­ного массива»¹⁰. Сюда же следует добавить метод «снежного кома».

Известный специалист по тендерной социологии Г.Г. Силласте¹' предлагает иную классификацию. У нее выборка подразделяется на вероятную (случайную) и целенаправленную. К первой относятся че­тыре метода: 1) собственно случайный отбор (для генсовокупности не более 800 единиц), который подразделяется на а) случайно-бесповтор­ный и б) случайно-повторный методы; 2) механическая выборка; 3) серийная выборка; 4) гнездовая выборка. Во вторую включены: 1) репрезентативная, 2) квотная и 3) стихийная выборки (рис. 2.1).

В статистической науке в зависимости от способа отбора раз­личают выборки следующих типов:

1) случайная выборка с возвратом;

2) случайная выборка без возврата;

3) механическая;

4) типическая;

5) серийная

В маркетинге, по мнению Е.П. Голубкова, при формировании выборки используются вероятностные (случайные) и невероятно­стные (неслучайные) методы. Если все единицы выборки имеют известный шанс (вероятность) быть включенными в выборку, то выборка называется вероятностной. Если эта вероятность неизве­стна, то выборка называется невероятностной. Вероятностные ме­тоды включают: простой случайный отбор, систематический от­бор, кластерный отбор и стратифицированный отбор. Простой случайный отбор может осуществляться с помощью следующих методов: формирование выборки вслепую и с помощью таблицы случайных чисел¹².

Обобщив разнообразные точки зрения, можно заключить, что во всех случаях типы выборки делятся на вероятностные (случай­ные) и невероятностные (неслучайные, целевые, целенаправлен­ные). Ярких представителей каждого типа немного, например, случайная безвозвратная выборка явно принадлежит первому 95

типу, а квотная наилучшим образом характеризует достоинства и недостатки второго, невероятностного типа. Гораздо больше та­ких видов и методов выборки, которые можно отнести к смешан­ным. Их можно включить и в первый и во второй типы, а можно отнести лишь к одному из них. Ошибки не будет и в том случае, если придумать некий третий тип, назвать его, допустим, комби­национным и занести туда смешанные виды. Их особенность со­стоит в том, что вероятностные приемы отбора в них присутству­ют частично — на одном из этапов, в нарушенном виде (смещен­ная выборка), в одном из элементов или приемов отбора. Их недостаток заключается в том, что репрезентативность получае­мой информации находится под вопросом. Хотя это вовсе не оз­начает, что смешанные типы выборки всегда нерепрезентативны. Они могут быть репрезентативными, а могут и не быть, поэтому объявлять такие типы выборки нерепрезентативными нельзя. В них сложно установить репрезентативность, используя класси­ческие статистические приемы. Но кто говорит, что в будущем на­ука не шагнет дальше, прибавив к традиционным какие-либо не­традиционные способы определения репрезентативности данных? Описав кратко проблему типологии выборочных методов, пе­рейдем к характеристике наиболее распространенных.

2.4. Методы вероятностной (случайной) выборки

Случайная (вероятностная) выборка — это выборка, для ко­торой каждый элемент генеральной совокупности имеет опре­деленную, заранее заданную вероятность быть отобранным. Это позволяет исследователю рассчитать, насколько правильно вы­борка отражает генеральную совокупность, из которой она вы­делена (спроектирована). Такую выборку иногда называют еще случайной.

Вероятностные методы включают:

♦ простой случайный отбор,

♦ систематический отбор,

♦ кластерный отбор,

♦ стратифицированный отбор.

Реализовать случайную выборку можно двумя приемами: ло­терейным методом и с помощью таблицы случайных чисел. С по­мощью случайной выборки строится подавляющее большинство телефонных опросов и опросов на основе избирательных списков. Для построения такой выборки необходимо иметь полный спи­сок всех элементов генеральной совокупности.

2.4.1. Простой случайный отбор

Простой случайный отбор предполагает, что вероятность быть включенным в выборку известна и является одинаковой для всех единиц совокупности. Он реализуется двумя методами:

♦ отбор вслепую (другое название — метод лотереи или жребия),

♦ отбор не вслепую (происходит с помощью таблицы случай­ных чисел).

Итак, в одном случае вы осуществляете свой выбор не глядя, в другом — все осознавая, но для того, чтобы самому не вмешать­ся и ничего не испортить, обращаетесь к специальным таблицам.

Кроме того, простой случайный отбор подразделяется на две разновидности уже по другому критерию, а именно — возвраще­нию или невозвращению лотерейного шара (вместо него может быть фамилия респондента) обратно в корзину. В этом случае выделяют:

♦ случайный повторный (с возвращением) отбор,

♦ случайный бесповторный (без возвращения) отбор.

В чем сходство и различие двух классификаций? В первом слу­чае — вслепую/не вслепую — ученый мог смотреть на то, как осу­ществляется отбор, хотя никак не мог ему помешать (если отбор проводился вслепую), или выбор осуществляли не его руки, вы­нимающие из корзины шар, а таблица случайных чисел. Во вто­ром случае — повторный/бесповторный — дело заключается не в исследователе (если отбор проводился не вслепую), а в лотерей­ном шаре: его либо возвращают для нового выбора, либо не воз­вращают и продолжают процесс без него.

Соединив оба членения простого случайного метода в декар-тову систему координат, получим четыре модальности (рис. 2.2).

Сразу оговоримся, что получившаяся схема не является в стро­гом смысле изображением логического квадрата, с помощью кото­рого принято показывать отношения совместимости, эквивалент­ности, противоположности (контрарности), частичной совместимо­сти (субконтрарности), подчинения и противоречивости суждений. В нашей схеме лишь некоторые квадраты дают новый тип случай­ного отбора или свидетельствуют о том, что данная комбинация действий осуществима. При использовании метода выборки всле­пую единицы генеральной совокупности (фамилии, названия или просто номера из списка) можно вносить в карточки, а карточки в перемешанном виде поместить в какую-то непрозрачную емкость (ящик, коробку). Из этой емкости кто-то случайным образом вы-тягивает число карточек, определяемое объемом выборки. После каждого вытягивания и регистрации карточки ее можно возвра-97

щать, а можно не возвращать назад. В первом случае говорят о по­вторном, во втором — о бесповторном отборе. Их комбинация дает два квадрата, имеющих реальное содержание: можно вслепую вы­бирать из корзины шары и возвращать их для нового выбора, а можно их откладывать в сторону. Однако выборка не вслепую пред­полагает использование таблицы случайных чисел. Возвращать в нее выбранный номер невозможно, стало быть, образуемые вдоль этой оси квадраты не являются реальными.

Предлагаемая схема выполняет скорее мнемоническую функ­цию, помогая лучше запомнить материал. Можно также считать, что она имеет демонстративный смысл, но никак не логический. Она придумана для того, чтобы внести какую-то ясность в типо­логию разновидностей простого случайного отбора.

Вероятностную выборку целесообразно применять только при наличии соответствующих условий. Первое условие осуществления вероятностной выборки — наличие полного списка всех элементов генеральной совокупности (отсутствие или недоступность которо­го чаще всего и препятствует ее реализации) от 1 до N, где N— общее число всех элементов. Если же он имеется, то производится нумерация, после чего можно использовать вышеописанные мето­дики. При использовании лотерейного метода (или метода жребия) жетоны с номерами всех элементов помещают в урну, тщательно перемешивают и извлекают последовательно п жетонов, где п — число элементов выборочной совокупности. Элементы генеральной совокупности, имеющие номера, оказавшиеся на извлеченных же­тонах, будут составлять выборочную совокупность. Это довольно

рудоемкая и продолжительная (при больших размерах выборки) операция, к тому же достаточно трудоемкая, поскольку «для обес­печения равного шанса выбора требуется тщательное перемешива­ние жетонов»¹³ после каждой выемки очередного номера.

Второе условие вероятностной выборки —хорошая перемешан-ность элементов генеральной совокупности. Если выборка элемен­тов производится из ящика, то его содержимое следует тщатель­но перемешать и уже после этого брать карточки случайным об­разом. Только при таких условиях все они имеют одинаковую вероятность попасть в выборку. Часто для образования случайной выборки элементы генеральной совокупности предварительно нумеруются, а каждый номер записывается на отдельной карточ­ке. В результате получается пачка карточек, число которых совпа­дает с объемом генеральной совокупности. После тщательного перемешивания из этой пачки берут по одной карточке. Объект (респондент), имеющий одинаковый номер с карточкой, счита­ется попавшим в выборку. При этом возможны два принципиаль­но различных способа образования выборочной совокупности.

Первый— вынутая карточка после фиксации ее номера возвра­щается в пачку, после чего карточки снова тщательно перемеши­ваются. Повторяя такие выборки по одной карточке, можно об­разовать выборочную совокупность любого объема. Выборочная совокупность, образованная по такой схеме, получила название случайной возвратной выборки.

Второй— каждая вынутая карточка после ее записи обратно не возвращается. Повторяя по такой схеме выборки по одной карточ-ке, можно получить выборочную совокупность любого заданного объема. Выборочную совокупность, образованную по данной схе-ме называют случайной безвозвратной выборкой. Она возможна лишь в том случае, если из тщательно перемешанной пачки сразу берут нужное число карточек.

Заметим, что различие между случайными выборками с возвра-том и без возврата стирается, если они составляют незначитель-ную часть большой генеральной совокупности.

Однако при большом объеме генеральной совокупности этот метод оказывается очень трудоемким, и поэтому гораздо удобнее пользоваться таблицей случайных чисел. Она доказала свою эф-фективность при формировании равновероятностной выборки из больших совокупностей. Фрагмент такой таблицы случайных чи-сел приведен в табл. 2.1.

			Фрагмент таблицы случайных чисел		Таблица	2.1

В таблицах случайных чисел все числа включены в таблицу слу­чайным образом. Единицам совокупности присваивают порядковые номера. В таблице выбирают любую начальную точку и, двигаясь в произвольном направлении и произвольно меняя направление дви­жения, выбирают необходимое количество номеров из числа присво­енных, равное заранее установленному объему выборки.

Если мы имеем, скажем, популяцию (т.е. генеральную сово­купность) из 1507 элементов и хотим спроектировать выборку из 150, мы можем выбирать любые четыре смежных столбца в таб­лице случайных чисел. Каждый раз, когда будет появляться чис­ло от 0001 до 1507, мы будем считать, что оно обозначает номер отбираемого элемента. Если число появляется более чем один раз, этот номер игнорируется после первого раза. Если мы начнем с первых четырех столбцов в табл. 2.1, спускаясь по столбцам, то в выборку будут включены элементы под номерами 0799,1016,0084, 480 и 1306. Поскольку мы не стремимся умышленно отыскать определенное число, мы можем начать с любого места таблицы и использовать любую систему для движения по таблице.

Сегодня таблицу случайных чисел могут заменить машинные устройства, например компьютер, снабженный специальной про­граммой. Их называют генераторами случайных чисел. При теле­фонном интервьюировании компьютер, имеющий генератор слу­чайных чисел, может подавать на экран случайным образом ото­бранные телефонные номера.

2.4.2. Систематический отбор

Систематический отбор является вторым по научной значимо­сти, но первым по популярности употребления видом простого случайного отбора. Его называют еще механическим отбором и считают упрощенным вариантом простого случайного отбора.

100

Примером служат разного рода квартирные выборки: выби­раются улицы, на которых интервьюер проводит квартирный оп­рос. Квартиры выбираются по определенной схеме (крайняя квартира справа от лестницы на последнем этаже первого подъез­да и т.д.).

Если под рукой таблицы случайных чисел нет, а генсовокупность относительно невелика¹⁴, то можно воспользоваться алфавитным списком, например, персонала предприятия (картотека всегда есть в отделе кадров) или избирательного участка (при опросе по месту жительства). Процедура систематического отбора проста: количе­ство единиц генеральной совокупности, предположим 2000 работ­ников предприятия, делится на количество анкет, скажем 200, и определяется шаг выборки. Он предполагает, что, начиная с любо­го номера из списка, опрашивается каждый десятый (2000:200 = 10). В формализованном виде данная процедура выглядит так. Из про­нумерованного списка через равные интервалы £ отбирается задан­ное число респондентов. При этом шаг выборки к рассчитывается по простой формуле:

 

 

где N— численность генеральной совокупности, п — численность выборочной совокупности.

Таким образом, шаг выборки, а его еще называют «интервалом скачка» или просто «интервалом», — это математический показа-тель, рассчитанный как отношение объема генеральной совокуп-ности к объему выборки. Он показывает, сколько номеров в спис-ке фамилий людей, вошедших в генеральную совокупность, надо пропустить (через сколько перешагнуть), чтобы в итоге получить список выборочной совокупности. Буквально шаг выборки озна-я чает расстояние между соседними фамилиями респондентов, из меренное количеством отбракованных фамилий из списка гене-ральной совокупности (рис. 2.3).

Другой пример. Предположим, что нам нужно спроектировать выборку численностью 100 из списка 5000 студентов какого-то вуза. Если мы намерены использовать систематическую выборку, то должны вначале рассчитать интервал выборки делением числа элементов в списке на размер выборки. В данном случае, разде­лив 5000 имен на требуемый размер выборки 100 ед., мы получим интервал (шаг) выборки 50. Так что мы будем систематически двигаться по списку и отбирать каждого пятидесятого студента (отобрав таким образом 100 имен). Определение того места в спис­ке, с которого мы начнем, проводится случайным образом, по таблице случайных чисел (это называется случайным стартом). Таким образом, если случайно выбрана точка старта под номером 31, то в выборку будут включены студенты, стоящие под номера­ми 31, 81, 131, 181 и т.д.

Итак, в основу систематической выборки положены не веро­ятностные процедуры, а алфавитные списки, картотеки, схемы, которые обеспечивают равновероятное попадание в выборку всех единиц генеральной совокупности.

Несмотря на свои преимущества, систематическая выборка мо­жет иногда иметь своим результатом предубежденную выборку. Такая ситуация возникает, например, когда элементы размещены в списке, ранжированном по каким-то характеристикам. В этой ситуации определение места начала случайного отбора будет вли­ять на средние характеристики всей выборки. Например, если сту­денты расставлены в списке в соответствии со средним оценоч­ным баллом от высшего к низшему, систематическая выборка, включающая студентов, стоящих в списке под номерами 1,51,101, будет иметь более низкий средний балл, чем выборка, включаю-Щая студентов под номерами 50, 100 и 150. Каждая новая выбор­ка будет давать другой средний балл, который представляет собой предубежденную картину студенческой популяции.