В данной задаче линейного программирования какая точка отвечает max, если вектор градиенты имеет координаты (1;1)
Вопросы контрольного тестирования блока СД (Специальных дисциплин) для специальности: 230105 Программное обеспечение вычислительной техники и автоматизированных систем
СД.01. Математические методы
1. Область допустимых решений задачи линейного программирования имеет вид:
Тогда максимальное значение функции 1. 11 2. 13 3. 10 4. 14
2. Дана транспортная задача:
При каком значении Z транспортная задача будет закрытой 1. 130 2. 185 3. 220 4. 210 3. Вектор градиента при решении задачи линейного программирования геометрическим методом имеет вид:
1. (3; -1) 2. (2; 5) 3. (-1; 3) 4. (1; -1) Для задачи линейного программирования
Двойственная задача имеет целевую функцию вида: 1. 2. 3. 4.
Длина критического пути сетевого графика, указанного на рисунке, равна.
1. 21 2. 17 3. 22 4. 23
6. В какой форме записана задача 1. канонической 2. общей 3. векторно-матричной 4. основной
7. Какая из следующих задач не является задачей линейного программирования: 1)
2)
3)
4)
В данной задаче линейного программирования какая точка отвечает max, если вектор градиенты имеет координаты (1;1)
1. E 2. G 3. F 4. C 9.Алгоритм пошагового решения присущ задаче: 1. линейного программирования 2. нелинейного программирования 3. динамического программирования 4. целочисленного программирования
Телевизионная компания планирует подключение к кабельной сети пяти новых районов. Структура планируемой сети и расстояния между пунктами (в км) заданы на рисунке.
1. 16 2. 13 3. 9 4. 25
11. В каких задачах целевая функция ограниченна на области допустимых значений? Вектор
12. Критический путь на сетевом графике содержит: 1. наиболее длительные работы 2. работы с нулевым резервом времени 3. все работы 4. начальное и конечное события
|


 равно:
равно:



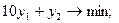








 - вектор градиент целевой функции.
- вектор градиент целевой функции.






