Додаток V
Значення коефіцієнтів a і b для розрахунку плит, обпертих по контуру
при рівномірно розподіленому навантаженні
| Спів-відношення сторін
| Схема 1
| Схема 2
| Схема 3
| Схема 4
| 
| aк1
| aд1
| aк2
| aд2
| bк2
| aк3
| aд3
| bд3
| aк4
| aд4
| bк4
| |
| 0,0365
| 0,0365
| 0,0334
| 0,0273
| 0,0892
| 0,0273
| 0,0334
| 0,0893
| 0,0267
| 0,018
| 0,0694
| | 1,1
| 0,0399
| 0,033
| 0,0349
| 0,0231
| 0,0892
| 0,0313
| 0,0313
| 0,0867
| 0,0266
| 0,0146
| 0,0667
| | 1,2
| 0,0428
| 0,0298
| 0,0357
| 0,0196
| 0,0872
| 0,0348
| 0,0292
| 0,082
| 0,0261
| 0,0118
| 0,0633
| | 1,3
| 0,0452
| 0,0268
| 0,0359
| 0,0165
| 0,0843
| 0,0378
| 0,0269
| 0,0760
| 0,0254
| 0,0097
| 0,0599
| | 1,4
| 0,0469
| 0,024
| 0,0357
| 0,014
| 0,0808
| 0,0401
| 0,0248
| 0,0688
| 0,0245
| 0,008
| 0,0565
| | 1,5
| 0,048
| 0,0214
| 0,035
| 0,0119
| 0,0772
| 0,042
| 0,0228
| 0,062
| 0,0235
| 0,0066
| 0,0534
| | 1,6
| 0,0485
| 0,0189
| 0,0341
| 0,0101
| 0,0735
| 0,0433
| 0,0208
| 0,0553
| 0,0226
| 0,0056
| 0,0506
| | 1,8
| 0,0485
| 0,0148
| 0,0326
| 0,0075
| 0,0668
| 0,0444
| 0,0172
| 0,0432
| 0,0208
| 0,004
| 0,0454
| |
| 0,0473
| 0,0118
| 0,0303
| 0,0056
| 0,061
| 0,0443
| 0,0142
| 0,0338
| 0,0193
| 0,003
| 0,0412
|
Продовження додатку V
|
Спів-відношення сторін
| Схема 5
| Схема 6
| Схема 7
| |
| aк5
| aд5
| bд5
| aк6
| aд6
| bк6
| bд6
| aк7
| aд7
| bк7
| bд7
| |
| 0,018
| 0,0267
| 0,0694
| 0,0269
| 0,0269
| 0,0625
| 0,0625
| 0,0266
| 0,0198
| 0,0556
| 0,0417
| | 1,1
| 0,0218
| 0,0262
| 0,0708
| 0,0292
| 0,0242
| 0,0675
| 0,0558
| 0,0234
| 0,0160
| 0,0565
| 0,035
| | 1,2
| 0,0254
| 0,0254
| 0,0707
| 0,0309
| 0,0214
| 0,0703
| 0,0488
| 0,0236
| 0,0142
| 0,056
| 0,0292
| | 1,3
| 0,0287
| 0,0242
| 0,0689
| 0,0319
| 0,0188
| 0,0711
| 0,0421
| 0,0235
| 0,012
| 0,0545
| 0,0242
| | 1,4
| 0,0316
| 0,0229
| 0,066
| 0,0323
| 0,0165
| 0,0709
| 0,0361
| 0,023
| 0,0102
| 0,0526
| 0,0202
| | 1,5
| 0,0341
| 0,0214
| 0,0621
| 0,0324
| 0,0144
| 0,0695
| 0,031
| 0,0225
| 0,0086
| 0,0506
| 0,0169
| | 1,6
| 0,0362
| 0,02
| 0,0577
| 0,0321
| 0,0125
| 0,0678
| 0,0265
| 0,0218
| 0,0073
| 0,0484
| 0,0142
| | 1,8
| 0,0388
| 0,0172
| 0,0484
| 0,0308
| 0,0096
| 0,0635
| 0,0196
| 0,0203
| 0,0054
| 0,0442
| 0,0102
| |
| 0,04
| 0,0146
| 0,0397
| 0,0294
| 0,0074
| 0,0588
| 0,0147
| 0,0189
| 0,004
| 0,0404
| 0,0076
|
Продовження додатку V
|
Спів-відношення сторін
| Схема 8
| Схема 9
| |
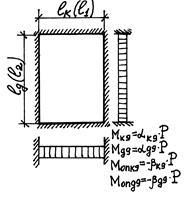
| aк8
| aд8
| bк8
| bд8
| aк9
| aд9
| bк9
| bд9
| |
| 0,0198
| 0,0226
| 0,0417
| 0,0556
| 0,0179
| 0,0179
| 0,0417
| 0,0417
| | 1,1
| 0,0226
| 0,0212
| 0,481
| 0,053
| 0,0134
| 0,0161
| 0,045
| 0,0372
| | 1,2
| 0,0249
| 0,0198
| 0,053
| 0,0491
| 0,0204
| 0,0142
| 0,0468
| 0,0325
| | 1,3
| 0,0266
| 0,0181
| 0,0565
| 0,0447
| 0,0208
| 0,0123
| 0,0475
| 0,0281
| | 1,4
| 0,0279
| 0,0162
| 0,0588
| 0,04
| 0,021
| 0,0107
| 0,0473
| 0,024
| | 1,5
| 0,0285
| 0,0146
| 0,0597
| 0,0354
| 0,0208
| 0,0093
| 0,0464
| 0,0206
| | 1,6
| 0,0289
| 0,013
| 0,0599
| 0,0312
| 0,0205
| 0,008
| 0,0452
| 0,0177
| | 1,8
| 0,0288
| 0,0103
| 0,0583
| 0,024
| 0,0195
| 0,006
| 0,0423
| 0,0131
| |
| 0,028
| 0,0081
| 0,0555
| 0,0187
| 0,0183
| 0,0046
| 0,0392
| 0,0098
|
Додаток VI
Формули для розрахунку двогілкових і ступінчатих колон
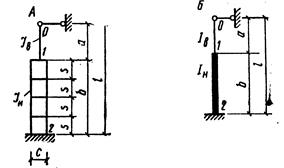
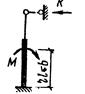
| Схема завантаження
| Опорна реакція R
| Схема завантаження
| Опорна реакція R
|
|
|
|
|
|
|
|
| 
|
| 
|
| 
|
| 
|
|
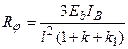
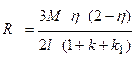
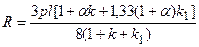
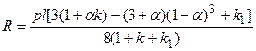
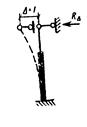
Позначення:  ;  ;  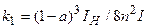;  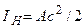(для двогілкових колон);  – площа перерізу гілки;  – кількість панелей двогілкової колони. Інші позначення на рис.А. У розрахунку ступінчатих колон (рис.Б) при визначенні реакції  для суцільних ступінчатих колон треба у формулах, наведених вище для двогілкових колон, прийняти  , а момент інерції  нижньої підкранової частини колони визначати як для суцільного прямокутного перерізу,  – момент інерції прямокутної гілки
Шрифт зодчего Шрифт зодчего состоит из прописных (заглавных), строчных букв и цифр...
|
Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|
Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|
Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|
Способы тактических действий при проведении специальных операций Специальные операции проводятся с применением следующих основных тактических способов действий: охрана...
Искусство подбора персонала. Как оценить человека за час Искусство подбора персонала. Как оценить человека за час...
Этапы творческого процесса в изобразительной деятельности По мнению многих авторов, возникновение творческого начала в детской художественной практике носит такой же поэтапный характер, как и процесс творчества у мастеров искусства...
|
Основные симптомы при заболеваниях органов кровообращения При болезнях органов кровообращения больные могут предъявлять различные жалобы: боли в области сердца и за грудиной, одышка, сердцебиение, перебои в сердце, удушье, отеки, цианоз головная боль, увеличение печени, слабость...
Вопрос 1. Коллективные средства защиты: вентиляция, освещение, защита от шума и вибрации Коллективные средства защиты: вентиляция, освещение, защита от шума и вибрации
К коллективным средствам защиты относятся: вентиляция, отопление, освещение, защита от шума и вибрации...
Задержки и неисправности пистолета Макарова 1.Что может произойти при стрельбе из пистолета, если загрязнятся пазы на рамке...
|
|
