Порядок выполнения работы и обработка результатов измерений
Для измерения линейных размеров тел сравнительно небольшой величины служат штангельциркуль и микрометр. После ознакомления с указанными приборами приступают к измерению. Упражнение 1. Измерение объема прямоугольного параллелепипеда. Определение плотности материала параллелепипеда. При помощи штангельциркуля измеряют длину а, ширину b и высоту с тела, имеющего форму прямоугольного параллелепипеда (рис. 1).
Из результатов трех измерений каждой величины вычисляют ее среднее значение. Таким путем получают средние значения линейных размеров тела:
Таблица №1
Если при измерении какой-либо величины все три результата получились одинаковыми, то абсолютная ошибка равна половине точности штангельциркуля. Если, например, точность штангельциркуля 0,1 мм, то абсолютная ошибка измерения равна 0,05мм. Затем вычисляют объем тела
Взвешиванием на простых (технических) весах определяют массу тела m с точностью до Вычисляют плотность вещества тела
Относительная ошибка при определении плотности параллелепипеда равна
Абсолютная ошибка равна
Окончательный результат определения плотности выражают в виде
Упражнение 2. Измерение объема цилиндра. Определение плотности материала цилиндра. При помощи микрометра измеряют диаметр цилиндра d три раза: около оснований цилиндра и в его средней части (рис. 2). Определяют средний диаметр Таблица №2
Высоту цилиндра h измеряют при помощи штангельциркуля один раз. Абсолютную ошибку Вычислить объем цилиндра:
Взвешиванием на весах определяют массу цилиндра m с точностью до Вычисляют плотность вещества цилиндра:
Абсолютная ошибка равна: Окончательный результат определения плотности вещества цилиндра записывают в виде:
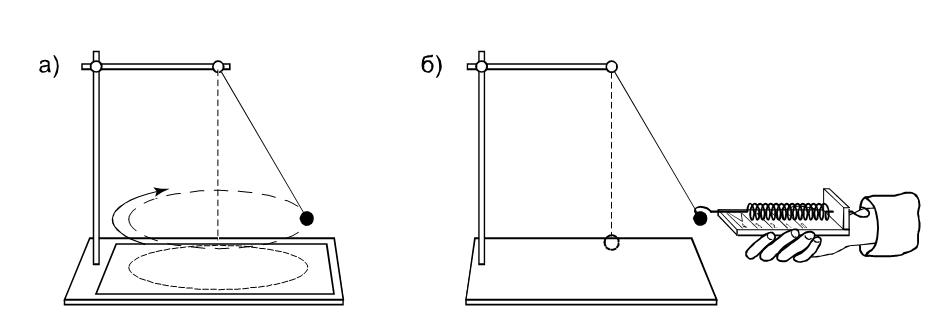
Вопросы для самоконтроля 1. Какие измерения называют прямыми, а какие – косвенными? 2. Чем отличаются методики расчёта ошибок для прямых и косвенных измерений? 3. В чём состоит принцип равной точности измерений и выполнен ли он в упражнениях 1 и 2? 4. Составьте формулу для расчёта относительной ошибки по предложенной преподавателем расчётной формуле некоторой косвенно определяемой физической величины. 5. Справедливо ли утверждение “Точность прямых измерений пропорциональна числу измерений”? Ответ обоснуйте. 6. Сформулируйте правило определения числа прямых измерений. Примените это правило к результатам ваших измерений. 7. Какая величина является асимптотой для средней абсолютной ошибки при увеличении числа измерений? 8. Чем определяется число значащих цифр при записи результатов расчётов среднего значения физ. величины и его средней абсолютной ошибки? 9. С какой точностью надо взять число при расчёте объёма цилиндра? 10. Как следует выбирать масштаб значений физических величин, откладываемых на осях графиков? 11. Каким образом на графиках отражают точность измерений и расчётов значений физических величин? 12. Какой линией, ломаной или плавной кривой, изображают на графиках зависимости значений функциональных физических величин от значений независимых физических величин? Ответ обоснуйте. ЛАБОРАТОРНОЙ РАБОТЫ № 2 Цель работы: определение центростремительного ускорения шарика при его равномерном движении по окружности. Теоретическая часть работы. Эксперименты проводятся с коническим маятником. Небольшой шарик движется по окружности радиуса R. При этом нить АВ, к которой прикреплен шарик, описывает поверхность прямого кругового конуса. На шарик действуют две силы: сила тяжести
Для определения ускорения надо измерить радиус окружности и период обращения шарика по окружности. Центростремительное (нормальное) ускорение можно определить также, используя законы динамики. Согласно второму закону Ньютона
Направление координатных осей выберем так, как показано на рисунке б. В проекциях на ось О1у уравнение движения шарика примет вид: 0 = F2 — mg. Отсюда F2 = mg: составляющая Запишем второй закон Ньютона в проекциях на ось О1х: man = F1. Отсюда
Отсюда Во-вторых, модуль составляющей F1 можно непосредственно измерить динамометром. Для этого оттягиваем горизонтально расположенным динамометром шарик на расстояние, равное радиусу R окружности (рис. в), и определяем показание динамометра. При этом сила упругости пружины уравновешивает составляющую Сопоставим все три выражения для аn:
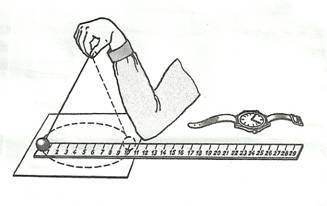
и убедимся, что они близки между собой. В этой работе с наибольшей тщательностью следует измерять время. Для этого полезно отсчитывать возможно большее число оборотов маятника, уменьшая тем самым относительную погрешность. Взвешивать шарик с точностью, которую могут дать лабораторные весы, нет необходимости. Вполне достаточно взвешивать с точностью до 1 г. Высоту конуса и радиус окружности достаточно измерить с точностью до 1 см. При такой точности измерений относительные погрешности величин будут одного порядка. Оборудование: штатив с муфтой и лапкой, лента измерительная, циркуль, динамометр лабораторный, весы с разновесами, шарик на нити, кусочек пробки с отверстием, лист бумаги, линейка. Указания к работе. 1. Определяем массу шарика на весах с точностью до 1 г. 2. Нить продеваем сквозь отверстие и зажимаем пробку в лапке штатива (рис. в). 3. Вычерчиваем на листе бумаги окружность, радиус которой около 20 см. Измеряем радиус с точностью до 1 см. 4. Штатив с маятником располагаем так, чтобы продолжение шнура проходило через центр окружности. 5. Взяв нить пальцами у точки подвеса, вращаем маятник так, чтобы шарик описывал окружность, равную начерченной на бумаге. 6. Отсчитываем время, за которое маятник совершает, к примеру, N = 50 оборотов. 7. Определяем высоту конического маятника. Для этого измеряем расстояние по вертикали от центра шарик; до точки подвеса. 8. Находим модуль центростремительного ускорение по формулам:
9. Оттягиваем горизонтально расположенным динамо метром шарик на расстояние, равное радиусу окружности, и измеряем модуль составляющей 10. Результаты измерений заносим в таблицу.
Сравнивая полученные три значения модуля центростремительного ускорения, сделать вывод:
|

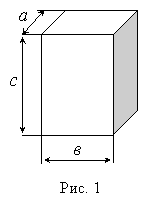 Каждую из величин а, b, с измеряют три раза: около граней тела и в его средней части. Результаты измерений записывают в таблицу.
Каждую из величин а, b, с измеряют три раза: около граней тела и в его средней части. Результаты измерений записывают в таблицу. и
и 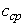 . После этого вычисляют абсолютные ошибки для каждого измерения
. После этого вычисляют абсолютные ошибки для каждого измерения  и находят их средние величины. Все полученные результаты заносят в таблицу.
и находят их средние величины. Все полученные результаты заносят в таблицу.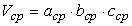
 = 0,1 г.
= 0,1 г.
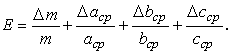
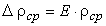
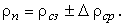
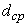 , абсолютные ошибки для каждого измерения и среднюю абсолютную ошибку
, абсолютные ошибки для каждого измерения и среднюю абсолютную ошибку 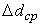 . Все результаты заносят в таблицу
. Все результаты заносят в таблицу 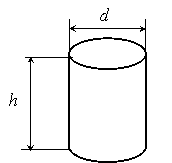 .
.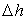 взять равной половине точности штангельциркуля
взять равной половине точности штангельциркуля 
 . Относительная ошибка при определении плотности цилиндра равна:
. Относительная ошибка при определении плотности цилиндра равна: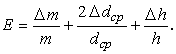
 (7)
(7)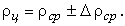
 и натяжение нити
и натяжение нити 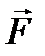 (рис. а). Они создают центростремительное ускорение
(рис. а). Они создают центростремительное ускорение  , направленное по радиусу к центру окружности. Модуль ускорения можно определить кинематически. Он равен:
, направленное по радиусу к центру окружности. Модуль ускорения можно определить кинематически. Он равен:
 . Разложим силу
. Разложим силу 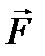 на составляющие
на составляющие 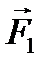 и
и 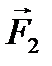 , направленные по радиусу к центру окружности и по вертикали вверх.
, направленные по радиусу к центру окружности и по вертикали вверх. Тогда второй закон Ньютона запишется следующим образом:
Тогда второй закон Ньютона запишется следующим образом:
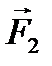 уравновешивает силу тяжести
уравновешивает силу тяжести  , действующую на шарик.
, действующую на шарик.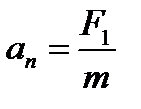
 Модуль составляющей F1 можно определить различными способами. Во-первых, это можно сделать из подобия треугольников ОАВ и FBF1:
Модуль составляющей F1 можно определить различными способами. Во-первых, это можно сделать из подобия треугольников ОАВ и FBF1:
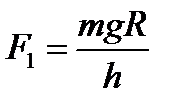 и
и 
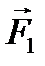 .
.
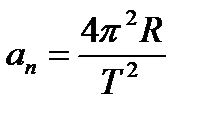 ,
, 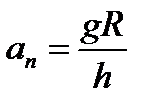 ,
, 


