Замечание.
При вычислении десятичного значения р -ичной дроби по развернутой форме с использованием калькулятора также целесообразно пользоваться схемой Горнера, что минимизирует количество арифметических действий и исключает возведение в степень. Пример 4. а) Перевести
Ответ: б) Перевести
Ответ: в) Перевести
Ответ: При переводе неправильной конечной р -ичной дроби в десятичную систему счисления необходимо перевести как целую, так и дробную части с помощью развернутой формы представления чисел. Пример 5. Перевести
Ответ: Замечание. Конечную р -ичную дробь не всегда можно представить в виде конечной десятичной дроби. Если нахождение значения десятичной дроби с помощью развернутой формы представления числа будет затруднено, то исходную дробь следует представить в виде обыкновенной дроби, в числителе которой будет развернутая форма числа, стоящего после точки (запятой), а знаменателем – р в соответствующей степени. Пример 6. а) Перевести
Ответ: б) Перевести
Ответ: Перевод правильной бесконечной периодической p -ичной дроби в десятичную систему счисления заключается в представлении исходной дроби в виде обыкновенной дроби, в числители которой будет записан период в развернутой форме, а знаменатель – р в соответствующей степени, уменьшенный на единицу. Пример 7. a) Перевести
Ответ: б) Перевести
Ответ: в) Перевести
Ответ: Перевод целого числа из десятичной системы счисления в p -ичную осуществляется последовательным целочисленным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе счисления записывается в виде остатков от деления в обратном порядке, начиная с последнего частного от деления. Пример 8. а) Перевести
Ответ: б) Перевести
Результат Перевод правильной конечной дроби из десятичной системы счисления в p -ичную осуществляетсяпоследовательным умножением на основание той системы, в которую она переводится до тех пор, пока дробная часть произведения не станет равной нулю, или не выделится период. При этом умножаются только дробные части. Дробь в новой системе счисления записывается в виде последовательности целых частей произведений, начиная с первого. Пример 9. а) Перевести
Ответ: б)Перевести
Ответ: При переводе неправильной конечной десятичной дроби в р -ичную систему счисления необходимо отдельно перевести целую часть и отдельно дробную, а затем их соединить. Пример 10. Перевести 1) Переведем целую часть:
2) Переведем дробную часть:
Таким образом Ответ: Необходимо отметить, что целые числа остаются целыми, а правильные дроби – правильными в любой системе счисления. Перевод бесконечной периодической десятичной дроби в р -ичную состоит в том, что периодическую дробь представляем в виде обыкновенной (числителем будет являться период, а знаменателем – 10 в степени, соответствующей количеству цифр периода, уменьшенным на единицу), затем целочисленные числитель и знаменатель переводим в р -ичную систему, далее делим числитель на знаменатель и получаем р -ичную дробь. Пример 11. a) Перевести
Ответ: б) Перевести
Ответ: Замечание. Конечной или бесконечной периодической десятичной дроби всегда соответствует или конечная, или бесконечная периодическая дробь в р -ичной системе счисления. Перевод бесконечной непериодической дроби (иррационального числа) возможно лишь с определенной степенью точности. Для перевода восьмеричного или шестнадцатеричного числа в двоичную систему счисления достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) или четырехразрядным двоичным числом (тетрадой) (таб. 1) и отбросить незначащие нули в старших и младших разрядах. Пример 12. а) Перевести
Ответ: б) Перевести
Ответ: Для перевода из двоичной в восьмеричную или шестнадцатеричную систему счисления поступают следующим образом: двигаясь от точки разделения целой и дробной части числа влево и вправо, разбивают двоичное число на группы по три или четыре разряда, дополняют при необходимости нулями крайние левую и правую группы. Затем триаду или тетраду заменяют соответствующей восьмеричной или шестнадцатеричной цифрой. Пример 13. а) Перевести
Ответ: б) Перевести
Ответ: Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад. Пример 14. Перевести
Ответ:
|

 .
.

 .
. .
.
 .
. .
.
 .
. .
.

 .
. .
.
 .
. .
.
 .
. .
.
 .
.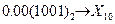 .
.
 .
. .
.
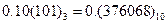 .
. .
.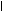



 .
. .
. 128
128
 .
.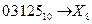 .
.
 8
8
 .
.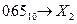 .
.
 .
.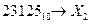 .
.

 ;
; 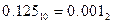 .
. .
. .
.
 .
. .
.
 .
.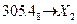 .
.
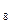 =
= 
 .
. .
.
 =
= 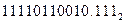 .
. .
. .
.


 .
.

 .
. .
.





 .
.


