Суммой событий А и В называется событие, которое происходит тогда и только тогда, когда происходит или А, или В или А и В одновременно, т.е. хотя бы одно из этих событий.
Суммой событий А и В называется событие, которое происходит тогда и только тогда, когда происходит или А, или В или А и В одновременно, т.е. хотя бы одно из этих событий. Произведением событий А и В называется событие АВ, которое происходит тогда и только тогда, когда происходят события А и В одновременно. Противоположным к событию А называется событие, которое происходит тогда и только тогда, когда событие А не происходит.
3. Полной группой называется такая группа событий, если в результате данного эксперимента обязательно произойдет хотя бы одно из этих событий. События называются несовместными, если они не могут произойти одновременно в результате данного эксперимента. События называются независимыми, если происхождение или непросхождение одного из них не изменяет вероятности происхождения второго.
4. Вероятность случайного события это численная мера объективной возможности происхождения случайного события.
5. Вероятность события невозможного равна 0: Вероятность события достоверного равна: Вероятность события противоположного к А равна: Р(А) = 1- Р( Вероятность случайного события может принимать значения от 0 до 1: 0
6. Число сочетаний без повторений из n по k – это число способов, сколькими можно из n различных элементов выбрать k штук без учета порядка. Формула для нахождения числа сочетаний без повторений имеет вид:
Свойства: 1) 3) 5)
7. Если количество элементарных исходов эксперимента конечное число и исходы равновозможны, то вероятность события А может быть найдена с помощью классического определения вероятности:
8. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий за вычетом вероятности их совместного происхождения, т. е.:
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т. е.:
Для трех совместных событий формула имеет вид:
Для трех несовместных событий формула имеет вид:
Вероятность произведения двух зависимых событий равна произведению вероятности первого события на вероятность второго, найденную при условии, что первое событие уже произошло т. е.:
Вероятность произведениядвух независимых событий равна произведению вероятностей этих событий, т. е.:
Для трех зависимых событий формула имеет вид:
Для трех несовместных событий формула имеет вид:
9. Если событие А не может произойти само по себе, а только после того, как произошло одно из событий
События
10. Если событие А уже произошло, то можно переоценить первоначальные вероятности гипотез
11. Пусть производится n независимых испытаний. В каждом из них может произойти событие А – успех, и Пусть число успехов, которые могут произойти в n испытаниях обозначено за k. Причем k = 0, 1, 2, …, n. Тогда вероятность того, что в n испытаниях будет ровно kуспехов –
12. Если число испытаний
13. Если число испытаний
где
14. Если число испытаний
где а
|

 Æ) = 0.
Æ) = 0. .
. ).
). 1.
1. .
. ; 2)
; 2)  ;
; ; 4)
; 4)  .
. ; 6)
; 6)  .
.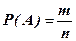 , где n – общее число исходов эксперимента, m – числоисходов,благоприятствующих для события А.
, где n – общее число исходов эксперимента, m – числоисходов,благоприятствующих для события А.
 .
.

 .
. .
. .
.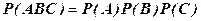 .
. , то вероятность события А находится по формуле полной вероятности:
, то вероятность события А находится по формуле полной вероятности: .
. .
.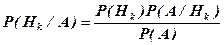 , k =1, 2, …, n
, k =1, 2, …, n – вероятность неудачи. Причем p + q = 1; p и q – const, т.е. не изменяются от испытания к испытанию.
– вероятность неудачи. Причем p + q = 1; p и q – const, т.е. не изменяются от испытания к испытанию. найдется по формуле Бернулли:
найдется по формуле Бернулли: .
.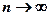 , а вероятность успеха
, а вероятность успеха 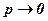 , то вероятность того, что в n испытаниях будет ровно kуспехов –
, то вероятность того, что в n испытаниях будет ровно kуспехов – 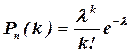 , где
, где  .
. (т. е. не стремится ни к 0, ни к 1), то вероятность того, что в n испытаниях будет ровно kуспехов –
(т. е. не стремится ни к 0, ни к 1), то вероятность того, что в n испытаниях будет ровно kуспехов – 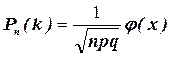 ,
, , а
, а  – локальная функция Лапласа.
– локальная функция Лапласа. до
до  –
– 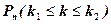 найдется с помощью интегральной теоремы Лапласа:
найдется с помощью интегральной теоремы Лапласа: ,
, ;
;  ,
,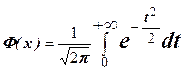 – интегральная функция Лапласа.
– интегральная функция Лапласа.


