In which the Wooden Midshipman gets into Trouble

Дата добавления: 2015-08-17; просмотров: 594

1. Изучить принципы работы генератора Г3-33 и электронного частотомера Ч3-34.

2. Измерить частоту электрического сигнала подаваемого с генератора (измерения проводить не менее 30 раз с интервалом 10 с).

3. Результаты занести в таблицу.

4. Выявить грубые погрешности для первых 10 измерений с использованием критерия Романовского. Для этого определить среднее значение и среднеквадратическое отклонение S по формулам:

;

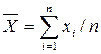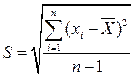
Результаты занести в таблицу 1.

Таблица 1. Результаты измерений и вычислений исследуемой величины

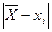
№ п/п	Значение величины xi	Отклонение от среднего	Квадрат отклонения
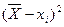
без учета хmax	без учета xmin	без учета xmax	без учета xmin
…
σх

Для наибольшего отклонения от среднего 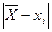- вычислить значение критерия Романовского по формуле (5). Если (K_P)_Э ≥ (K_P)_T, то соответствующий результат при доверительной вероятности P = 0,95 и числе измерений n =10 считается промахом и исключается из выборки. В этом случае необходимо проверить следующий, менее отличающийся от среднего результат по аналогичной методике.

5. Найти грубые погрешности для 30 измерений с применением критерия «трех сигм». Расчет проводить по методике аналогичной приведенной для критерия Романовского. Если K_3σ > 3, то соответствующий результат считается промахом и исключается из выборки.

6. Определить наличие грубых погрешностей с использованием критерия Шовене. Расчет проводить по методике приведенной выше.

7. Сформулировать общие выводы по работе, т.е. установить наличие или отсутствие в выборке грубых погрешностей.

Контрольные вопросы:

1. Что называют случайной погрешностью?

2. Что называется систематической погрешностью?

3. Какую составляющую итоговой погрешности возможно исключить из результата измерения?

3. Как можно исключить систематические погрешности измерений?

4. Что является грубыми погрешностями и какие причины приводят к их возникновению?

5. Как применяется критерий Романовского для исключения грубых погрешностей выборки?

6. Расскажите об использовании вариационного критерия Диксона для нахождения промахов.

7. Как применяется критерий Шовене для исключения грубых погрешностей выборки?

8.Как применяется критерий "3σ" для исключения грубых погрешностей выборки?

Литература:

1 Сытько В.В. Теоретическая метрология. 1. Физические величины и их

измерение. Мн., - 1998.

2 Сергеев А.Г., Крохин В.В. Метрология: Учебное пособие для вузов. - М.:

Логос, 2001.

3 Маркин Н.С. Введение в метрологию. - М.: Издательство стандартов, 1991.

4 Тойберг П. Оценка точности результатов измерений. - М.: Энергоатомиздат,

1988.

5 Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений.

- М.: Энергоатомиздат, 1990.

Лабораторная работа № 6

Приближение многочленами таблично заданных функций в Mathcad (метод наименьших квадратов)

Цели работы:

· научиться интерполировать функции в Mathcad, используя вычислительный алгоритм метода наименьших квадратов;

· научиться рассчитывать и анализировать величину среднеквадратичного отклонения;

· освоить приемы иллюстрации решения графиками.

Задача наименьших квадратов возникает при обработке экспериментальных данных. Простейшая задача, приводящая к приближению (аппроксимации) функций, заключается в следующем. На некотором отрезке 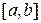заданы n+1 точки 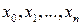и приближенные значения некоторой функции 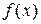в этих точках

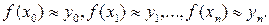
Требуется построить функцию 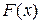(аппроксимирующая функция), принимающая в заданных точках 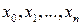значения, близкие к 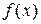. В такой общей постановке задача может иметь бесчисленное множество решений или совсем не иметь решений. Задача становится однозначной, если вместо произвольной функции 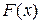искать полином степени не выше m. Необходим критерий выбора полинома , являющегося лучшим приближением к 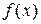. При решении поставленной задачи методом наименьших квадратов критерием приближения является требование минимизации среднеквадратического уклонения.

Используя аппроксимирующую функцию (найденный степенной многочлен), обычно находят промежуточные значения заданной табличной функции. Такая операция называется интерполированиемфункции 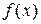. Если же необходимо найти значение функции 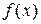в точке 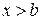, такая операция называется экстраполяцией. Рассмотрим, как это делается методом наименьших квадратов.