Стаття 165. Майно виробничого кооперативу

Дата добавления: 2015-10-15; просмотров: 673

Решение систем линейных уравнений

Пример: решить систему линейных уравнений

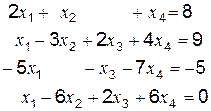
Решение возможно одним из способов (s₁, s₂, s₃ или s₄ – см. приведенную ниже программу).

--> a=[2, 1, 0, 1; 1, -3, 2, 4; -5, 0, -1, -7; 1, -6, 2, 6]; b=[8 9 -5 0];

--> s1=b/a', s2=a\b', s3=b*a'^(-1), s4=b*inv(a')

s1 =

8.1481481 - 1.5185185 11.703704 - 6.7777778

s2 =

8.1481481

- 1.5185185

11.703704

- 6.7777778

s3 =

8.1481481 - 1.5185185 11.703704 - 6.7777778

s4 =

8.1481481 - 1.5185185 11.703704 - 6.7777778

Решить систему линейных уравнений вида 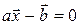можно с помощью функции linsolve : linsolve(a,b). В нашем примере:

a=[2, 1, 0, 1; 1, -3, 2, 4; -5, 0, -1, -7; 1, -6, 2, 6]; b=[8; 9 ;-5 ;0]; x=linsolve(a,-b)

x =

8.1481481

- 1.5185185

11.703704

- 6.7777778

Если система уравнений имеет бесчисленное множество решений, то выводится одно из них:

a=[2, 1; 4, 2]; b=[-7; -14 ];x=linsolve(a,b)

x =

2.8

1.4

Если система не имеет решений:

a=[2, 1; 4, 2]; b=[-7; -13 ];x=linsolve(a,b)

WARNING:Conflicting linear constraints!

x =

[]

Вопрос №9

Вычисление корней полинома

Функция roots(c) возвращает вектор-столбец из корней полинома с.

Пример: решить уравнение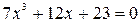

--> x=[7, 0, 12, 23]; d=roots(x)

d =

0.5564046 + 1.6257442i

0.5564046 - 1.6257442i

- 1.1128093

Примечание: Коэффициенты полинома следует вводить в порядке убывания степеней переменной x. Если в уравнении отсутствует слагаемое, содержащее, например, x², то в векторе коэффициентов на соответствующем месте надо ввести 0.

Вопрос №10

Решение нелинейных уравнений вида f(x)=0

Уравнения бывают алгебраическими и трансцендентными. Алгебраическим называют уравнение вида 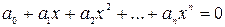. Если уравнение нельзя свести к алгебраическому заменой переменных, то его называют трансцендентным. Пример: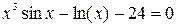

Для решения уравнений, в том числе трансцендентных, в Scilab применяют функцию fsolve(x0,f)

где x0 - начальное приближение, f - функция, описывающая левую часть уравнения f(x)=0.

Пример: решить уравнение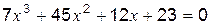

Набираем в окне редактора файл:

function y=f(x)

y=7*x.^3+45*x.^2+12*x+23;

endfunction

и сохраняем его под именем f.sci.Загружаем его в Scilab(Execute/Load into Scilab).

Для нахождения отрезка [a, b], на котором отделен корень данного уравнения, построим график функции .

-->x=-8:0.1:-5; plot(x, f(x)); xgrid()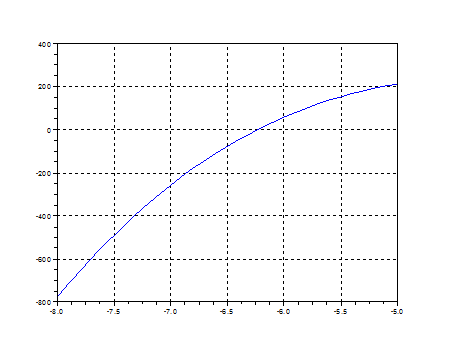

Из графика видно, что корень отделен на отрезке [-6.5 , -6]. Найдем его, используя функциюfsolve:

-->x0=-6.5;x1= fsolve(x0,f)

Получаем:

x1 =

- 6.2381997

Систему нелинейных уравнений также можно решить, используя функцию fsolve.

clc

function [y]=ff(x)

y(1)=x(1)^2+x(2)^2-1;

y(2)=x(1)^3-x(2);

endfunction

t=fsolve([-.5,-.5],ff)

t =

- 0.8260314 - 0.5636242