
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Стаття 854. Порядок оплати роботи
Дата добавления: 2015-10-15; просмотров: 705
|
|
2. Выполните матричные вычисления задание 1.
2.1.Выполните сложения, вычитания и умножения (скалярные) матриц А и В.
2.2.Транспонировать матрицы А і В.
2.3.Вычислить скалярный и векторный произведения векторов матриц А і В (для вычиления выбрать произвольные три вектора матрицы А и три – матрицы В).
2.4.Найдите обратные матрицы А і В.
3. Задание 2: Решить систему линейных уравнений Ах=b тремя способами: методом обратной матрицы, методом Гаусса и методом Крамера.
Метод обратной матрицы.
3.1.введите матрицу коэффициентов A(n,m), где n количество строк, m –количество столбцов,
3.2.введите столбец свободных членов b(n) (обратите внимание, столбец правых частей вводится именно как столбец, а не строка),
3.3.рассчитайте по формуле x=A-1b (результат вектор значений х),
3.4.проверьте результат, с этой целью исходную матрицу коэффициентов A системы умножим на найденное решение (вектор x) и получим, как и должны были, правый столбец b. Для того, чтобы он был выведен в виде строки, воспользуйтесь операцией транспонирования.
4. Метод Крамера.
4.1.введите матрицу коэффициентов A,
4.2.введите столбец свободных членов b,
4.3.присвойте матрице А1 значения матрицы А,
4.4.в матрице А1 замените 1 столбец на столбец b,
4.5.найдите определитель пеобразованной матрицы А1, присвойте полученное значение элементу массива d(1),
4.6.повторите пункты 4.3 – 4.5 и определите А2, d(2) … ,
4.7. найдите вектор х = d/определитель исходной матрицы А.
Метод Гаусса.
5.1. получите новую матрицу С путем преобразования исходной матрицы и столбца свободных членов с помощью функции rref(A,b), (получите справку по этой функции, узнайте ее действия)
5.2. вектор х последний столбец матрицы С.
Сравните результаты трех методов решения системы линейных уравнений.
Сохраните расчеты во встроенном редакторе SciNotes в трех файлах. Запустите какой-нибудь из файлов на выполнение.
8. Задание 3. Матрицы и вектор заполняются случайными числами от –10 до и 10 округляются до десятых (размерность матриц и соответственно вектора одинаковые). Выполите задание согласно варианта.
Сохраните вычисления.
Варианты заданий 1
| № | Матриці | № | Матриці |
А 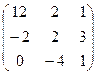 В В 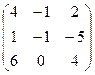
| А 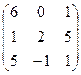 В В 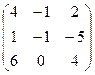
| ||
А 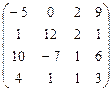 В В 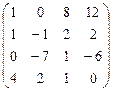
| А 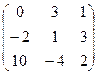 В В 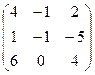
| ||
А  В В 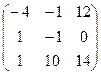
|
А 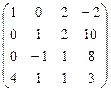 В В 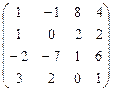
| ||
А 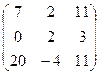 В В 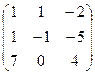
|
А 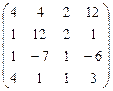 В В 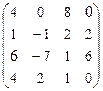
| ||
А 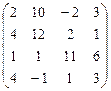 В В 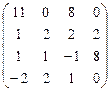
| А 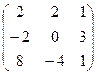 В В 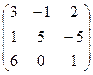
| ||
А 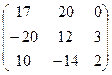 В В 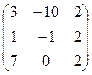
| А 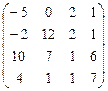 В В 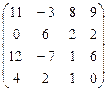
| ||
А 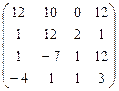 В В 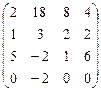
| А 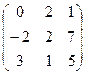 В В 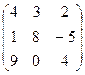
| ||
А 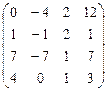 В В 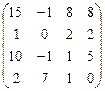
| А 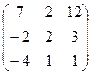 В В 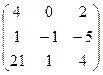
| ||
А 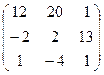 В В 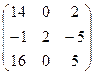
|
А 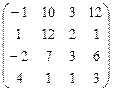 В В 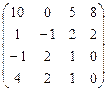
| ||
А  В В 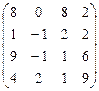
| А 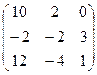 В В 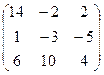
|
Варианты заданий 2
| № | Система лінійних рівнянь |
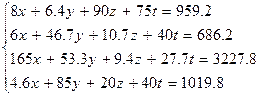
| |
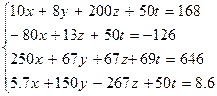
| |
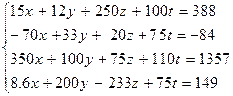
| |
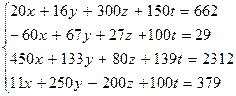
| |
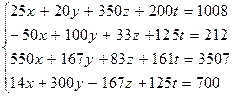
| |
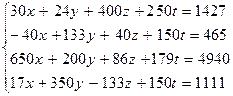
| |
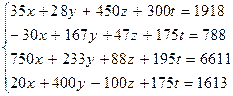
| |
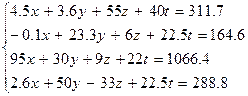
| |
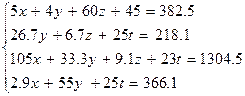
| |
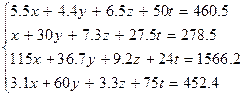
| |
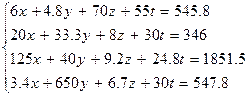
| |
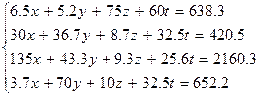
| |
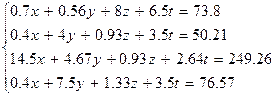
| |
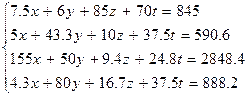
| |
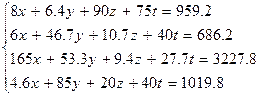
| |
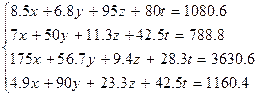
| |
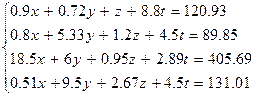
| |
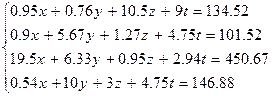
| |
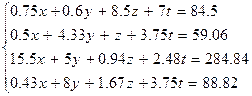
| |
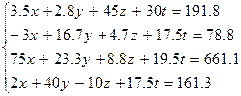
|
Варианты заданиий 3
1. Уведіть довільну матрицю розміром (4*6). Відшукайте суму найбільших елементів її рядків.
2. Уведіть квадратну матрицю (5*5) із єдиним найменшим елементом. Відшукайте суму елементів рядка, у якому розміщений елемент із найменшим значенням.
3. Уведіть матрицю (6*9), у якій є єдині найбільший і найменший елементи і вони розташовані у різних рядках. Поміняйте місцями рядки з найбільшим і найменшим елементами.
4. Уведіть матрицю (5*6) із різними значеннями елементів. У кожному рядку виберіть найменший елемент, з отриманих чисел виберіть найбільше. Знайдіть індекси отриманого елемента.
5. Уведіть матрицю (5*6). Побудуйте вектор, елементами якого є найбільші елементи відповідних рядків матриці.
6. Уведіть матрицю (5*6). Побудуйте вектор, елементами якого є суми найбільшого й найменшого елементів відповідних рядків матриці.
7. Уведіть матрицю (5*6). Побудуйте вектор, елементами якого є середні значення елементів відповідних рядків матриці.
8. Уведіть матрицю (5*6). Побудуйте вектор, елементами якого є середньоквадратичні відхилення елементів відповідних рядків матриці від їхнього середнього значення.
9. Уведіть матрицю (5*6). Побудуйте вектор, елементами якого є середні арифметичні значення найбільшого й найменшого елементів відповідних рядків матриці.
10.Уведіть матрицю (6*5). Побудуйте вектор, елементами якого є суми квадратів елементів відповідних стовпців матриці.
11. Уведіть матрицю (5*5). Побудуйте вектор, елементами якого є суми квадратів елементів відповідних стовпців матриці.
12. Уведіть матрицю (5*6). Відшукайте середнє арифметичне найбільшого й найменшого її елементів.
13. Уведіть матрицю (5*5). Побудуйте вектор, елементами якого є елементи головної діагоналі матриці. Відшукайте слід матриці.
14. Уведіть дві матриці (4*4). Побудуйте нову матрицю розміром (4*8), включаючи у перші 4 стовпчика рядки першої матриці, а в інші – рядки другої матриці.
15. Відшукайте суму усіх елементів матриці розміром (4*3).
| <== предыдущая лекция | | | следующая лекция ==> |
| Стаття 835. Припинення договору позички | | | Стаття 919. Строк доставки вантажу, пасажира, багажу, пошти |