Черкаси 2009 2 страница· методи апроксимації функції, які передбачають заміну початкової функції більш простою, та проведення обчислень з використанням спрощеного опису функції (метод хорд, метод Ньютона), дані методи швидше сходяться до розв‘язку. Швидкість збіжності метода характеризує відношення
2.1. Етап 1: відокремлення коренів
Рис. 2.1. Графічний спосіб відокремлення коренів.
Побудову графіка вдається значно спростити, якщо замінити рівняння (2.1) рівносильним йому рівнянням F1(х)= F2(х). В цьому випадку будують графіки функцій F1(х) та F2(х), потім на вісі OX відмічають відрізки, що вміщують абсциси точок перетину цих Рис. 2.2. Варіанти розв’язання рівняння при заміні функції рівносильними функціями F1(х) та F2(х) на визначеному проміжку.
Рис.2.3. Реальна функція F1(і) та її наближений аналог-функція F2(і).
При написанні програми, яка виконує відокремлення коренів графічний спосіб не є зручним, тому застосовують найпростіший алгоритм відокремлення коренів: проміжок, на якому відшукуються розв’язки, ділять рівномірно на невеликі відрізки, на кінцях кожного відрізку розраховують значення функції, якщо функція на кінцях відрізку змінює знак – відрізок містить корінь (значення початку і кінця відрізку записується для подальшої обробки), інакше – кореня на відрізку немає і відрізок ігнорується. Величина відрізків поділу залежить від коефіцієнта гладкості функції. Для визначення відрізку, що вміщує один корінь, можемо скористатися наступною теоремою [5]. Теорема 2.1. Якщо функція у = F(х) неперервна на інтервалі [a, b] і якщо F(а) та F(b) мають протилежні знаки, тобто F(а)× F(b) < 0, то F(х) має хоча б один дійсний корінь на інтервалі [a, b]. Якщо при цьому F(х) має першу похідну, що не змінює знак на інтервалі [a, b], то корінь єдиний.
2.2. Етап 2: уточнення коренів 2.2.1. Метод половинного ділення Припустимо, що рівняння
Рис. 2.4. Знаходження кореня рівняння методом половинного ділення.
Ітераційний процес продовжуємо, поки довжина відрізка не стане менше заданої точності
При оцінюванні похибки методу, можемо помітити, що вибираючи в якості розв‘язку ліву (a) чи праву (b) границю остаточно розрахованого проміжку, допускаємо, що розв‘язок може знаходитись на відстані, що не перевищує розмір проміжку, тобто меншій чи рівній Метод половинного ділення є абсолютно збіжним до розв‘язку, оскільки його алгоритм не залежить від виду функції
2.2.2. Метод хорд Даний метод ґрунтується на лінійній інтерполяції функції F(x)=0 по двох точках, що мають протилежні знаки у значеннях функції F(a) та F(b) (рис. 2.5). Метод хорд швидше попереднього збігається до розв‘язку навіть при досить малих значеннях e.
Рис. 2.5. Знаходження кореня за методом хорд.
Наприклад, потрібно знайти корінь рівняння F(x)=0 на проміжку [a; b], і відомо, що F(x) неперервна на [a; b] та F(a)∙ F(b) < 0. Крім того, перша F'(x) і друга F''(x) похідні функції F(x) зберігають на проміжку [a; b] свій знак. Замінимо функцію F(x) лінійною функцією, яка проходить через вузлові точки (a, F(a)) і (b, F(b)):
Лінійна функція P(x) на кінцях відрізку [a; b] приймає такі ж значення, як і функція F(x)=0. В якості першого наближення при знаходженні кореня функції F(x)=0 візьмемо точне значення кореня функції P(x)=0, тобто х1, яке розрахуємо з рівняння:
При подальшому дослідженні відрізків [a; х1] та [х1; b], виберемо той, на якому функція змінює знак. На рисунку 2.5 бачимо, що таким відрізком є [a; х1] Для вибраного відрізка побудуємо лінійне наближення функції за формулою 2.7, виконаємо розрахунки кореня для лінійного наближення за формулою 2.8, в результаті розрахунків отримуємо координати точки х2. Ітераційний процес продовжуємо до отримання істинності нерівності: Метод хорд має високу збіжність до розв‘язку навіть для таких функцій F(x)=0, які мають низькі показники гладкості, але в окремих випадках швидкість збіжності може знижатись, наприклад, на тих ділянках, де значення функції змінюється дуже повільно.
2.2.3. Метод січних Метод січних подібний до методу хорд, тільки точки з координатами (х0, F(х0)) та (х1, F(х1)) взяті з одного боку від кореня рівняння F(x)=0. Геометрична інтерпретація методу представлена на рис. 2.6. В якості початкового наближення обираємо точки (х0, f(x0)) та (х1, f(x1)). Через точки (х0, f(x0)) та (х1, f(x1)) проводимо січну до графіку функції, яка перетинає вісь х в точці (х2, 0). Перевіряємо виконання умови
Рис. 2.6. Знаходження кореня за методом січних.
Для математичного опису методу січних отримаємо формулу прямої, що проходить через дві точки (хn-1, f(xn-1)) та (хn, f(xn)):
Враховуючи, що f (xn+1) = 0 отримаємо загальну формулу для методу січних:
Метод січних має досить високу збіжність до розв‘язку у випадку, коли F(x)=0 гладка функція, але в процесі розв’язання деяких рівнянь швидкість збіжності може знижатись, наприклад, на ділянках функції, близьких до функції х = const.
2.2.4. Метод дотичних (Ньютона) Метод дотичних базується на заміні функції F(x)=0 у точці початкового наближення х0 дотичною, яка при перетині з віссю х в точці (х1, 0) дає перше наближення. У цьому методі Ньютон замість інтерполяції використав екстраполяцію, що знаходиться за допомогою дотичної у визначеній точці. Геометрична інтерпретація методу дотичних (Ньютона) показана на рисунку 2.7. В якості початкового наближення обираємо абсцису х0 = b. У точці (х0, f(x0)) проводимо дотичну до графіку функції, яка перетинає вісь х в точці (х1, 0). Перевіряємо виконання умови
Ітераційний процес продовжуємо до виконання умови виходу, тобто 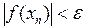 . .
Рис. 2.7. Знаходження кореня за методом дотичних.
Для математичного опису методу дотичних отримаємо формулу дотичної, що проведена в точці (х0, f(x0)) і має кутовий коефіцієнт
У точці перетину цієї дотичної з віссю х (точка (х1, 0)) y = 0, тому формулу 2.11 можемо записати у вигляді:
Для будь якого кроку ітераційного процесу формулу Ньютона можемо записати у вигляді:
Метод дотичних (Ньютона) має високу збіжність до розв‘язку, але час виконання ітерації дещо збільшується за рахунок необхідності обчислення похідної
2.2.5. Метод простої ітерації Замінимо рівняння
Припустимо w – корінь рівняння, а x0 – отримане будь-яким способом нульове наближення до кореня w. Підставимо x0 в праву частину рівняння (2.14), отримаємо ітераційну послідовність: Теорема 2. Ітераційна послідовність буде збіжною при будь-якому початковому значенні з інтервалу x0Î [a; b], якщо для рівняння x=f(x), що має єдиний розв’язок на проміжку [a, b], виконуються умови: 1) f(x) визначена для всіх xÎ [a, b]; 2) f(x) диференційована на відрізку [a, b]; 3) існує таке дійсне q, яке задовольняє нерівності Умови теореми є достатніми, але не являються необхідними, тому при їх невиконанні, іноді, ітераційна послідовність може виявитися збіжною до розв‘язку. Швидкість збіжності характеризується нерівністю:
де Умовою припинення ітерацій є нерівність (умова Ліпшиця):
Для забезпечення умови збіжності ітераційного процесу проведемо перетворення рівняння
З умов виконання третього пункту теореми 2 припустимо, що
Достатньо підібрати значення m так, щоб для всіх
Контрольні питання 1. Назвіть види функціональних рівнянь з однією змінною. 2. Що значить розв‘язати задачу в теорії чисельних методів? 3. З яких етапів складається розв‘язання задачі знаходження коренів функціонального рівняння з однією змінною? 4. Які методи реалізації другого етапу розв‘язання функціональних рівнянь мають абсолютну збіжність до розв‘язку? 5. В чому полягає суть алгоритму реалізації методу відокремлення коренів? 6. Сутність методу половинного ділення. Особливості обрання остаточного розв‘язку. 7. Сутність методу хорд. Умова виходу з ітераційного процесу. 8. Сутність методу січних. Від яких факторів і чому залежить швидкість збіжності методу? 9. Сутність методу дотичних (Ньютона). З чим пов‘язана швидкість обчислень за алгоритмом методу дотичних? 10. Сутність методу простої ітерації. Які умови повинні виконуватися для забезпечення збіжності методу? 11. Як потрібно перетворити рівняння за умовою збіжності методу простої ітерації? Розділ 3. Прямі та непрямі методи розв’язання систем лінійних алгебраїчних рівнянь. Методи Гауса та LU-розкладу
3.1. Основні поняття Математичні моделі багатьох технічних задач представлені системами лінійних рівнянь. Багато методів розв’язання нелінійних задач також зводяться до розв’язання деякої послідовності систем лінійних алгебраїчних рівнянь (СЛАР). Для багатьох методів розроблений математичний апарат, що дозволяє оцінити точність отриманого розв’язку. Чисельні методи розв’язку СЛАР поділяються на прямі (точні) та непрямі (ітераційні, наближені). Прямі (точні) методи дозволяють розв’язати систему рівнянь за скінчене число арифметичних операцій. Якщо всі операції виконуються точно (без помилок округлення), то розв’язок заданої системи також отримуємо точним. До прямих методів належать: метод послідовного виключення невідомих (метод Гауса та його модифікації: метод головного елемента, метод квадратного кореня, метод відображень та ін.), метод ортогоналізації, метод LU-розкладу. Прямі методи застосовують на практиці для розв’язання СЛАР за допомогою обчислювальної техніки, як правило, з числами порядку не вище 103 [5]. Ітераційні методи є наближеними. Вони дозволяють знайти розв’язок системи, як межу послідовних наближень, що обчислюються по однаковому алгоритму. Для застосування ітераційних методів у початкових умовах необхідно задати точність обчислень Розглянемо систему m лінійних алгебраїчних рівнянь з n невідомими:
Коротко її можна записати в матричному вигляді:
де
Розв’язком системи ЛАР називається така впорядкована сукупність чисел х1= с1, х2 = с2, … хn = сn, яка перетворює всі рівняння системи у істинні рівняння. Система ЛАР називається сумісною, якщо вона має хоча б один розв’язок, і несумісною – якщо вона не має розв’язків. Сумісна система називається визначеною, якщо вона має один розв’язок, і невизначеною, якщо має більше одного розв’язку.
3.2 Прямі методи розв‘язання систем лінійних алгебраїчних рівнянь 3.2.1. Метод Гауса Розглянемо систему лінійних алгебраїчних рівнянь (СЛАР):
в якій матриця коефіцієнтів А = (аij) не вироджена. Метод Гауса полягає у послідовному виключенні невідомих, тобто його суть у перетворенні системи (3.3) в систему з верхньою трикутною матрицею, з якої послідовно (при зворотному розв‘язку, тобто від останнього рівняння до першого) отримують значення всіх невідомих. Алгоритм послідовного виключення невідомих може бути побудований за різними обчислювальними схемами. Побудуємо його по схемі єдиного ділення. Перетворимо систему (3.3): припустимо а11 ¹ 0, розділимо всі коефіцієнти першого рівняння на а11. Віднімемо від кожного наступного рівняння системи перше рівняння, що помножене на коефіцієнт при х1. Не змінюючи першого рівняння, зробимо аналогічні перетворення над всіма іншими рівняннями системи. На другому етапі перетворень припустимо а22 ¹ 0, розділимо коефіцієнти другого рівняння на а22. Віднімемо від кожного наступного рівняння системи друге рівняння, що помножене на коефіцієнт при х2. Не змінюючи другого рівняння, зробимо аналогічні перетворення над всіма іншими рівняннями системи. Такі перетворення будемо проводити, поки не отримаємо систему з трикутною матрицею:
Із системи рівнянь (3.4) послідовно знаходимо значення всіх невідомих хn, хn-1, …, х1. Таким чином процес розв‘язання системи (3.3) за методом Гауса можна розділити на два етапи: 1) перший етап полягає в послідовному виключенні невідомих (приведенні матриці коефіцієнтів А = (аij) до верхньої трикутної матриці). Його називають прямим ходом. 2) другий етап – безпосереднє отримання значень невідомих, як результату розв’язання низки рівнянь однією змінною – називають зворотнім ходом. Таку назву етап отримав, оскільки розв‘язання починають із n -го, тобто останнього рівняння, послідовно проводячи розрахунки з n-1, n-2, n-3…3, 2, 1 рівняннями. В ході виконання операцій ділення в методі Гауса виникає обчислювальна похибка, яка при збільшенні кількості операцій (≥ 40) може значно спотворювати результат. Для зменшення обчислювальної похибки застосовують перестановки рівнянь у системі в залежності від головного елементу. Головним елементом називають максимальний коефіцієнт рівняння. Сукупність рівнянь в системі потрібно переставити таким чином, щоб на головній діагоналі матриці коефіцієнтів стояли максимальні по модулю елементи. Метод Гауса у такій модифікації називається методом Гауса з вибором головного елементу. 3.2.2. Метод LU-розкладу При розв‘язанні системи лінійних алгебраїчних рівнянь даним методом матрицю коефіцієнтів А розкладають на добуток двох матриць (формула 3.5) нижньої трикутної матриці L, на головній діагоналі якої стоять одиниці, та верхньої трикутної матриці U, елементи головної діагоналі якої не дорівнюють нулю. У матричному вигляді при n = 4 це можна записати таким чином:
Для розкладання матриці коефіцієнтів А на трикутні матриці використаємо метод виключення Гауса. Отримаємо матрицю L з допомогою одиничної матриці. Для цього помножимо зліва матрицю А на одиничну матрицю. Наприклад:
Перший рядок матриці А використовуємо для обнуління елементів першого стовпчика цієї ж матриці. Помножимо перший рядок на –0, 5 і віднімемо від другого, помножимо перший рядок на 0, 25 і віднімемо від третього рядка. Використані коефіцієнти для перетворень запишемо на місця елементів одиничної матриці, що відповідають індексам обнулених елементів матриці А. В результаті отримаємо:
Другий рядок матриці А використовуємо для обнуління елементів другого стовпчика цієї ж матриці, що знаходяться нижче другого рядка (у матриці, що утворена з одиничної, запишемо використаний для обнулення коефіцієнт на місце елементу, що відповідає індексам обнуленого елементу матриці А):
В результаті отримаємо LU-розклад матриці А і розв’яжемо систему рівнянь у два етапи:
На першому етапі знаходимо проміжний вектор Y, використовуючи пряму підстановку, на другому етапі знаходимо безпосередньо вектор розв’язків Х, застосовуючи зворотну підстановку. Зокрема, приймаючи у наведеному прикладі
3.2.3. Зв‘язок методу Гауса з методом LU - розкладу Алгоритм методу Гауса можна записати у матричному вигляді. Він полягає у розкладанні матриці коефіцієнтів А на добуток більш простих матриць. Для наочності розглянемо систему лінійних алгебраїчних рівнянь, що складається з 3-х рівнянь:
Для виключення невідомої х1 з другого і третього рівнянь системи (3.10) виконаємо наступні операції: § ділення першого рівняння на а11 = 0, § віднімання перетвореного першого рівняння, помноженого на а21 та а31 відповідно від другого і третього рівнянь. Перша з цих операцій еквівалентна множенню системи рівнянь зліва на діагональну матрицю:
Друга операція еквівалентна множенню зліва на матрицю:
Таким чином, для виключення невідомої х1 з другого і третього рівнянь системи (3.10) потрібно виконати наступне перетворення:
В результаті отримаємо систему рівнянь:
Другий крок прямого ходу методу Гауса, який полягає у виключенні невідомої х2 з третього рівняння, можемо виконати, помноживши систему рівнянь на матрицю:
В результаті отримаємо наступну систему рівнянь:
Для останнього кроку прямого ходу методу Гауса помножимо рівняння з раніше виконаними перетвореннями
Таким чином, сукупність виконаних перетворень можемо записати у вигляді:
Їх результатом є верхня трикутна матриця U з одиничною головною діагоналлю:
|

 , яке менше одиниці. У відношенні
, яке менше одиниці. У відношенні  , де х – точне значення розв‘язку, хk – чергове наближення до кореня. Чим менша величина даного відношення, тим швидше метод збігається до розв‘язку.
, де х – точне значення розв‘язку, хk – чергове наближення до кореня. Чим менша величина даного відношення, тим швидше метод збігається до розв‘язку. Відокремлення коренів полягає у встановленні „тісних” проміжків, кожен з яких вміщує тільки один корінь. Найбільш наочно про демонструвати цей етап можливо графічно. Враховуючи, що дійсні корені рівняння (2.1) – це точки перетину графіка функції F(х) з віссю абсцис, достатньо побудувати графік F(х) (рис.2.1) і відмітити на осі OX відрізки, кожен з яких вміщує лише один корінь.
Відокремлення коренів полягає у встановленні „тісних” проміжків, кожен з яких вміщує тільки один корінь. Найбільш наочно про демонструвати цей етап можливо графічно. Враховуючи, що дійсні корені рівняння (2.1) – це точки перетину графіка функції F(х) з віссю абсцис, достатньо побудувати графік F(х) (рис.2.1) і відмітити на осі OX відрізки, кожен з яких вміщує лише один корінь. графіків (рис. 2.2.).
графіків (рис. 2.2.).
 має на відрізку [a, b] єдиний корінь. Функція F(x) на цьому відрізку неперервна. Поділимо відрізок [a, b] точкою
має на відрізку [a, b] єдиний корінь. Функція F(x) на цьому відрізку неперервна. Поділимо відрізок [a, b] точкою  навпіл (рис.2.4). Якщо F(c) = 0, то розв’язок рівняння
навпіл (рис.2.4). Якщо F(c) = 0, то розв’язок рівняння  . Якщо F(c) ¹ 0, то вибираємо відрізок [a, с] чи [с, b], на якому функція змінює знак, тобто F(а)× F(с) < 0 чи F(с)× F(b) < 0. Для подальших поділів використовуємо цей відрізок. На кожному кроці процесу половинного ділення відрізок зменшується вдвічі.
. Якщо F(c) ¹ 0, то вибираємо відрізок [a, с] чи [с, b], на якому функція змінює знак, тобто F(а)× F(с) < 0 чи F(с)× F(b) < 0. Для подальших поділів використовуємо цей відрізок. На кожному кроці процесу половинного ділення відрізок зменшується вдвічі.
 :
: (2.6)
(2.6) , тому в даному випадку при реалізації алгоритму для досягнення заданої точності
, тому в даному випадку при реалізації алгоритму для досягнення заданої точності  .
. .
.
 Þ
Þ  (2.7)
(2.7) Þ
Þ  (2.8)
(2.8) .
. , якщо вона не виконується, проводимо січну через точки (х1, f(x1)) та (х2, f(x2)), знаходимо точку перетину січної з віссю х (точка (х3, 0)) і перевіряємо виконання чергової умови
, якщо вона не виконується, проводимо січну через точки (х1, f(x1)) та (х2, f(x2)), знаходимо точку перетину січної з віссю х (точка (х3, 0)) і перевіряємо виконання чергової умови  . Ітерації продовжуємо до виконання умови виходу з ітераційного процесу, тобто
. Ітерації продовжуємо до виконання умови виходу з ітераційного процесу, тобто  .
.
 (2.9)
(2.9) (2.10)
(2.10) , якщо вона не виконується, проводимо дотичну в точці (х1, f(x1)), знаходимо точку перетину дотичної з віссю х (точка (х2, 0)) і перевіряємо виконання чергової умови
, якщо вона не виконується, проводимо дотичну в точці (х1, f(x1)), знаходимо точку перетину дотичної з віссю х (точка (х2, 0)) і перевіряємо виконання чергової умови  .
.
 :
: (2.11)
(2.11) Þ
Þ 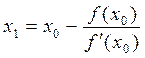 (2.12)
(2.12) (2.13)
(2.13) .
. рівносильним рівнянням:
рівносильним рівнянням: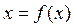 (2.14)
(2.14) . Таку числову послідовність називають послідовністю наближень. Послідовність наближень може бути збіжною чи розбіжною, і цей факт можемо визначити за наступною теоремою [6].
. Таку числову послідовність називають послідовністю наближень. Послідовність наближень може бути збіжною чи розбіжною, і цей факт можемо визначити за наступною теоремою [6]. для всіх
для всіх  .
. (2.15)
(2.15) – початкове значення змінної х;
– початкове значення змінної х;  – поточне значення змінної х, тобто значення на k -й ітерації;
– поточне значення змінної х, тобто значення на k -й ітерації;  – точний розв‘язок рівняння.
– точний розв‘язок рівняння. (2.16)
(2.16) до ітераційного вигляду:
до ітераційного вигляду: (2.17)
(2.17) , тоді отримаємо рівняння:
, тоді отримаємо рівняння: (2.18)
(2.18) , тобто при рівності правої і лівої частин
, тобто при рівності правої і лівої частин  для xÎ [a, b].
для xÎ [a, b]. (3.1)
(3.1) (3.2)
(3.2)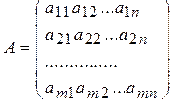 матриця m × n;
матриця m × n;  – вектор n -го порядку;
– вектор n -го порядку;  – вектор m -го порядку.
– вектор m -го порядку. (3.3)
(3.3) (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6)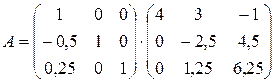 (3.7)
(3.7) (3.8)
(3.8) (3.9)
(3.9)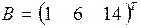 з проміжної системи LY = B матимемо
з проміжної системи LY = B матимемо  . Здійснюючи другий етап розв‘язання системи, тобто розв‘язуючи рівняння UX = Y, отримаємо
. Здійснюючи другий етап розв‘язання системи, тобто розв‘язуючи рівняння UX = Y, отримаємо  .
. (3.10)
(3.10)

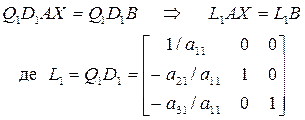 (3.11)
(3.11) (3.12)
(3.12)
 (3.13)
(3.13) на матрицю:
на матрицю:
 .
.



