Черкаси 2009 3 страницаСистема рівнянь (3.12) після перетворень матиме вигляд:
Оскільки
а нижня трикутна матриця Таким чином, отримані матриці
3.3 Непрямі методи розв‘язання систем лінійних алгебраїчних рівнянь
3.3.1. Забезпечення збіжності ітераційного процесу Непрямі (ітераційні, неточні) методи дозволяють наближено знайти розв’язок системи лінійних алгебраїчних рівнянь, як границю послідовних наближень, що обчислюються за певним алгоритмом. До ітераційних методів належать: метод Зейделя, метод простої ітерації, метод релаксації, градієнтні методи та їх модифікації. Застосовуються ітераційні методи для розв’язання СЛАР з коефіцієнтами порядку 106. Ознакою ітераційного методу розв‘язання системи ЛАР є наявність початкового наближення х0 чи (х01, х02, х03, …) і потрібної точності отримання розв‘язків e. Для успішного застосування ітераційних методів до початку ітерацій потрібно напевне знати, що ітераційний процес буде збігатися до конкретного розв‘язку. Для цього початкову систему приводять до нормалізованого вигляду таким чином:
Після заміни початкової системи лінійних рівнянь еквівалентною їй – нормалізованою системою – застосуємо ітераційні чисельні методи розв‘язання СЛАР, забезпечивши, таким чином, збіжність ітераціного процесу до розв‘язку.
3.3.2. Метод простої ітерації та метод Зейделя для розв‘язання систем лінійних алгебраїчних рівнянь
Першим необхідним корком при застосуванні методів простої ітерації та Зейделя є приведення системи лінійних алгебраїчних рівнянь до нормалізованого вигляду, представленого формулою 3.15. Для здійснення ітераційного процесу нормалізовану систему приводимо до ітераційного вигляду, тобто виражаємо з кожного і -го рівняння відповідну змінну хі:
Для початку ітерацій задаємо початкові значення всіх невідомих х1, х2, х3, … хn-1, хn. Метод простих ітерації полягає у підстановці значень вектору початкових наближень (х10, х20, х30, …, хn0) в праву частину системи (3.16) і отримання в лівій частині чергового вектора наближень (х11, х21, х31, …, хn1). Збіжність методу простих ітерацій досить повільна, для її підвищення Зейдель запропонував підстановку, яка дозволяє в (n-1) раз зменшити кількість кроків і, таким чином, підвищити збіжність методу. При здійсненні ітерацій підстановка Зейделя полягає в тому, що знайшовши з першого рівняння х11 по значеннях вектору початкових наближень інших змінних, ми використовуємо його при отриманні значення х21 у складі вектора чергових наближень (х11, х20, х30, …, хn0). Тобто всі попередньо знайдені значення поточної ітерації використовуються для знаходження наступних значень цієї ж ітерації. Ітераційний процес можна записати наступним чином:
Умовою припинення ітерацій є виконання нерівностей
3.3.3. Метод релаксації для розв‘язання систем лінійних алгебраїчних рівнянь
Даний метод є ітераційним і для його успішного застосування потрібно забезпечити збіжність ітераційного процесу до розв‘язку, для чого приведемо початкову систему лінійних алгебраїчних рівнянь до нормалізованого вигляду, представленого формулою 3.15. Перед початком першої ітерації перетворюємо нормалізовану систему до канонічного вигляду (формула 2.3). Для початку обчислень вибираємо початкове наближення (х10, х20, …, хn0 ) і точність обчислень e. На першому етапі обчислюємо, так звані, нев‘язки, тобто відхилення від нуля параметрів
які при канонічному представленні системи рівнянь повинні дорівнювати нулю. В системі знаходимо рівняння з максимальною по модулю нев‘язкою:
де і – номер рівняння з максимальною по модулю нев‘язкою. На наступному кроці підраховуємо нев‘язки за оновленим вектором наближень (х11, х20, …, хn0) і вибираємо рівняння з максимальною по модулю нев‘язкою
після чого розраховуємо
При знаходженні чергового значення Розрахунки продовжуємо до знаходження всіх значень Якщо умова не виконується розпочинаємо наступний цикл ітерацій, який проводиться так, як і попередній, але в якості початкових значень невідомих виступають значення, обчислені у попередньому циклі ітерацій, наприклад: (х31, х21, …, хn1). Цикли ітерацій продовжуємо до отримання необхідної точності e, яка визначається за простою умовою При реалізації методу релаксації рівняння намагаються вибирати в такому порядку, щоб за найменшу кількість кроків знайти розв‘язок із заданою точністю. Оскільки такий вибір є невизначеним даний метод називають нестаціонарним [7].
Контрольні питання 1. Якими методами розв‘язують системи лінійних алгебраїчних рівнянь? 2. В яких випадках варто застосовувати точні методи розв‘язку СЛАР? 3. В чому полягає сутність методу LU-розкладу? 4. В чому сутність зв‘язку методів Гауса і LU-розкладу? 5. Який обов‘язковий етап потрібно виконати перед розв‘язанням СЛАР неточними (ітераційними) методами? Для чого потрібен даний етап? 6. Сутність методу простої ітерації для розв‘язання СЛАР. 7. Чим метод Зейделя відрізняється від методу простої ітерації при розв‘язанні СЛАР? 8. Сутність методу релаксації для розв‘язання СЛАР. Як регулюється точність розв‘язків в даному методі? 9. Чому при розв‘язанні СЛАР методом релаксації виникають нев‘язки? 10. Чому метод релаксації є нестаціонарним? Розділ 4. Розв‘язання систем нелінійних рівнянь. Метод Ньютона
Не існує прямих методів розв‘язання нелінійних та трансцендентних рівнянь. Розв‘язання таких рівнянь складається з двох етапів: відокремлення коренів та їх уточнення. Процедура розв‘язання починається з вибору початкової точки х0 і обчислення нев‘язки рівняння f(х0 ). Якщо e < f(х0) вибирається алгоритм, за яким проводиться уточнення розв‘язків (при цьому використовується інформація про знак нев‘язки, її значення, або про швидкість її зміни f(х0 )/dx). Для розв‘язання нелінійних та трансцендентних рівнянь можуть застосовуватися звичайний ітераційний метод. Але при знаходженні розв‘язків збіжність ітераційного методу до конкретного розв‘язку залежить від початкових значень змінних [7]. Також складно вибрати функції fi, які б задовольняли умову збіжності Метод Ньютона оснований на знаходженні послідовності {[ x1k, x2k, …, xnk ]}, що збігається до розв‘язку (x1, x2, …, xn). Цей метод називають ітерацією нерухомої точки. Величина похідної в нерухомій точці визначає, чи буде ітераційний процес збіжним (теорема 4.1). Коли це правило застосовується для функції декількох змінних – похідні повинні бути частинними. Узагальненням похідної для системи функцій є матриця Якобі (Якобіан). Наприклад, для функцій трьох незалежних змінних f1(x, y, z), f2(x, y, z), f3(x, y, z) матриця Якобі має вигляд:
Для функцій декількох змінних диференціал використовується, щоб показати, як змінення незалежних змінних (
Допустимо, що значення цих функцій відомі в точці
де
Збіжність поблизу нерухомої точки. Ітерацію нерухомої точки визначаємо наступним чином [4]:
Теорема 4.1. Припустимо, що функції (4.2) та їх перші частинні похідні неперервні в області, в якій знаходиться нерухома точка
то ітерація збігається до нерухомої точки
Дана теорема визначає достатню умову збіжності, але вона не є необхідною. Так деякі системи нелінійних алгебраїчних рівнянь можуть сходитися до розв‘язку при невиконанні умови (4.6). Таку систему нелінійних рівнянь розглянемо у прикладі 4.1., що наведений нижче. Метод Ньютона виконується за наступними етапами: 1етап: для здійснення обчислень сформуємо функцію:
2 етап: обчислимо Якобіан:
3 етап: розв‘яжемо систему рівнянь:
Якщо матриця Якобі не вироджена, то розв‘язок системи запишемо у вигляді:
4 етап: обчислимо координати наступної точки – наступне наближення до розв‘язку має вигляд:
При графічному представленні процесу розв‘язання системи нелінійних алгебраїчних рівнянь методом Ньютона початкову точку розглядаємо в якості опорної, Якобіан визначає напрямок вектору до наступної точки розв‘язку, а значення функції, обчислене по даним початкової точки, – величину кроку у визначеному Якобіаном напрямку. Приклад 4.1. Розв‘яжемо систему нелінійних рівнянь:
Початкові значення для даної системи нелінійних рівнянь при розв‘язанні методом Ньютона: Сформуємо вектор-функцію і обчислимо матрицю Якобі:
В початковій точці вони приймуть значення:
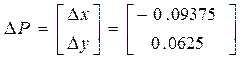
Обчислимо Dх, Dу з лінійної системи рівнянь:
Значення невідомих знаходять будь-яким, переважно точним, методом для розв‘язання систем лінійних рівнянь:
Розрахуємо значення координат наступної точки:
Аналогічно знайдемо два наступні розв‘язки:
Ітерації продовжуємо до досягнення заданої точності обчислень. В розглянутому прикладі точність обмежувалася чотирма десятковими знаками після коми, оскільки
Для розв‘язання систем нелінійних рівнянь можемо також застосовувати нелінійний ітераційний метод Зейделя [6], який передбачає незалежне розв‘язання кожного нелінійного рівняння системи відносно однієї (чергової) змінної, як це виконувалося і для систем лінійних алгебраїчних рівнянь (розділ 3, п. 3.3.2). Контрольні питання 1. В чому полягає суть методів розв‘язання систем нелінійних та трансцендентних рівнянь? 2. Розкрийте фізичний сенс Якобіана. 3. За яких умов ітерації в методі Ньютона збігаються до нерухомої точки? Чому дана умова є достатньою? 4. З яких етапів складається алгоритм методу Ньютона для розв‘язання нелінійних та трансцендентних систем рівнянь? 5. В чому полягає особливість програмної реалізації алгоритму методу Ньютона для розв‘язання нелінійних та трансцендентних систем рівнянь? 6. Яким чином застосовується метод Зейделя для розв‘язання систем нелінійних алгебраїчних рівнянь? Розділ 5. Інтерполяція функцій. Інтерполяційні поліноми Лагранжа. Сплайн-інтерполяція
На практиці часто приходиться розв‘язувати задачі, в яких складні функції простіше обчислити по їх наближеним аналогам [8]. Наприклад, для обчислення стандартних функцій sin(x), cos(x), ex в пакетах прикладних програм використовуються обчислювальні процедури, які ґрунтуються на заміні заданої функції наближеними функціями, побудованими на основі поліномів n–го порядку. Ще одним прикладом застосування поліномів є випадок, коли функція задана у вигляді таблиці вузлових точок. Для відображення поданих значень функцією і подальшому застосуванні цієї функції у розрахунках, будують поліноміальну криву y = P(x), що проходить через вузлові точки (для обчислення поліноміальної кривої повинен бути визначений проміжок, на якому будується наближення). За допомогою такої функції можливо знайти наближені значення в точках, що не є вузловими. Якщо така точка знаходиться у межах інтервалу наближення Припустимо, що функція f(x) задана таблицею значень f(x0), f(x1), f(x2), …, f(xn) для деякої кінцевої множини аргументів xi (вузлові точки) і при розв‘язуванні задачі потрібно використовувати значення функції f(x) у проміжних точках. Для апроксимації функції f(x) використовують функцію j(x), яку будують так, щоб у заданих точках x0, x1, x2, …, xn вона приймала значення, які збігаються зі значеннями f(x0), f(x1), f(x2), …, f(xn), а в інших точках відрізку [a, b] приблизно зображувала функцію f(x). Ступінь точності опису визначається в залежності від вибраного методу апроксимації. Найчастіше функцію j(x) будують у вигляді поліному. Теорема Веєрштрасса [8] стверджує, що функція f(x) може бути досить добре наближена за допомогою полінома деякого порядку m на множині точок x0, x1, x2, …, xn. Функцію j(x), яка наближує вихідну функцію f(x), у загальному випадку можна записати у вигляді:
де с0, с1, …, сm – деякі константи. Функція f(x) вважається наближено описана поліномом j(x), якщо f(x) і j(x) мають однакові значення у вузлових точках. Іноді, якщо функція і поліном диференційовані на проміжку наближення [a, b], вимагають збігу у вузлах похідних f(x) і j(x) визначених порядків. На практиці в якості базисних функцій { j(x) } обирають послідовність степеневих функцій відносно х: 1, x, x2, x3, …, xm, тобто j(x0)=1, j(x1)=х, j(x2)=х2, …, j(xm)=хm. В такому випадку поліном запишемо у вигляді:
Для знаходження коефіцієнтів сi використаємо умову j(xj) = f(xj), j = 0, 1, …, n і складемо систему рівнянь з (n+1) алгебраїчного рівняння.
Якщо m = n, система рівнянь (3) має єдиний розв‘язок за умови, що вектори Якщо m = n і в якості базисних функцій { j(x) } вибрати степеневі функції, то система рівнянь матиме вигляд:
Визначник цієї системи, який називають визначником Вандермонда [6]:
який не перетворюється в нуль, якщо серед сукупності вузлів немає повторень. У такому випадку матриця коефіцієнтів системи рівнянь є не виродженою і система має єдиний розв‘язок. В якості базисних функцій можемо вибрати також послідовність показникових функцій [9]:
де
5.1. Кусково-лінійна інтерполяція. Інтерполяційні поліноми вищих порядків. Інтерполяційний поліном Лагранжа
Найпростішим прикладом побудови інтерполяційного поліному є кусково-лінійна інтерполяція. При такому інтерполюванні будується відрізок прямої, яка проходить через дві сусідні вузлові точки (рис. 5.1). Рис. 5.1. Кусково-лінійна інтерполяція.
Тангенс кута нахилу між цими точками
При побудові інтерполяційної функції необхідно, щоб початкова функція
Інтерполяційний поліном Лагранжа. Французький математик Жозеф Луї Лагранж (1736-1813 р.р.) запропонував для побудови інтерполяційних поліномів наступний метод. Для двох вузлових точок
Відношення при
Інтерполяційний поліном Лагранжа має вигляд:
Він дозволяє досить просто побудувати наближення функції по відомим вузловим точкам у випадку невеликої кількості точок. Зі збільшенням числа точок
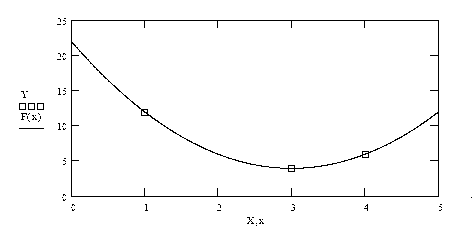
Наприклад: таблично задана функція:
Ступінь поліному n = 2. Складемо інтерполяційний поліном Лагранжа для функції з трьох вузлових точок:
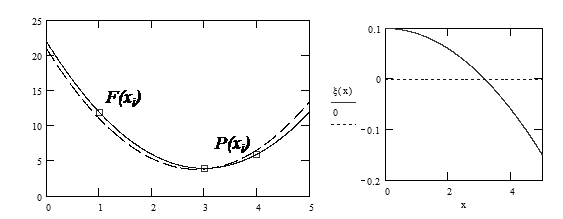
Графік, що відображає результати опису функції, представлений на рис. 5.2. Рис. 5.2. Результати апроксимації поліномом Лагранжа функції, що задана таблицею.
Рис. 5.3. Функція помилки апроксимації функції F(х) поліномом Р(х).
Похибку інтерполяційного поліному Лагранжа можна оцінити за формулою [4]:
При апроксимації складних функцій одним поліномом, такий поліном описує функцію з досить великими помилками:
|

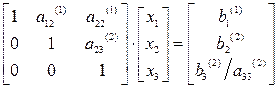 (3.14)
(3.14)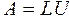 , то потрібно обчислити
, то потрібно обчислити  . Матрицю
. Матрицю 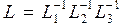 . Обернені матриці
. Обернені матриці 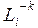 мають наступний вигляд:
мають наступний вигляд: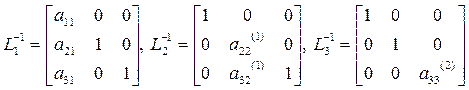
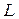 запишеться так:
запишеться так: 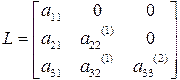 .
.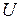 є дзеркальним відображенням одноіменних матриць, які використовувалися в класичному варіанті методу
є дзеркальним відображенням одноіменних матриць, які використовувалися в класичному варіанті методу 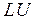 -розкладу (п.3.2.2). Отримані матриці
-розкладу (п.3.2.2). Отримані матриці 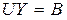 ; 2)
; 2) 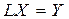 .
.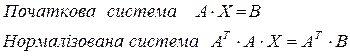 (3.15)
(3.15)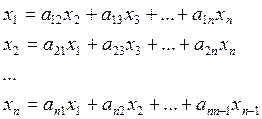 (3.16)
(3.16)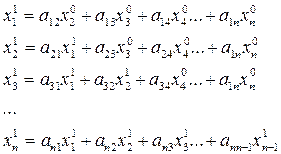 (3.17)
(3.17)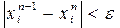 для всіх змінних хі. При виході з ітераційного процесу можемо констатувати, що розв‘язок знайдено з точністю e.
для всіх змінних хі. При виході з ітераційного процесу можемо констатувати, що розв‘язок знайдено з точністю e.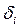 :
: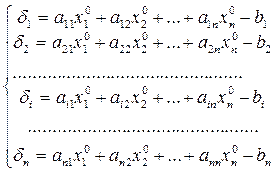 , (3.18)
, (3.18) , і, обнулюючи
, і, обнулюючи  за формулою:
за формулою: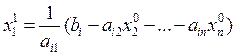 (3.19)
(3.19)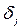 :
: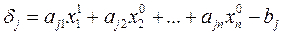 , (3.20)
, (3.20)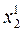 , що задовольняє рівності:
, що задовольняє рівності: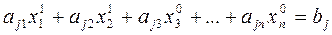 (3.21)
(3.21)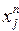 не забувайте обнулювати
не забувайте обнулювати 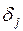 !
!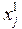 , після цього перевіряємо умову припинення ітерацій, яка записується у вигляді:
, після цього перевіряємо умову припинення ітерацій, яка записується у вигляді: 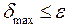 .
.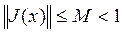 , де J - матриця Якобі, що визначається формулою 4.1. Тому для розв‘язання систем нелінійних і трансцендентних рівнянь застосовують узагальнений метод Ньютона (далі – метод Ньютона).
, де J - матриця Якобі, що визначається формулою 4.1. Тому для розв‘язання систем нелінійних і трансцендентних рівнянь застосовують узагальнений метод Ньютона (далі – метод Ньютона).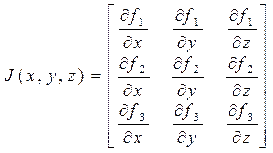 (4.1)
(4.1)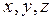 ) вплине на залежні змінні (
) вплине на залежні змінні (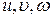 ). Наприклад, задані функції:
). Наприклад, задані функції: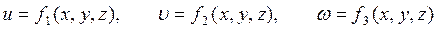 (4.2)
(4.2)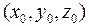 і необхідно визначити їх значення в точці
і необхідно визначити їх значення в точці 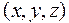 віддаленій на
віддаленій на 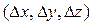 .
.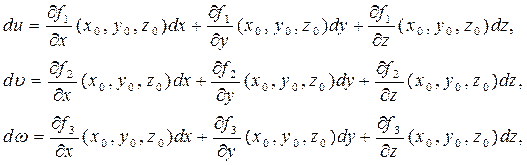 (4.3)
(4.3)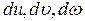 – диференціали залежних змінних,
– диференціали залежних змінних, 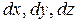 – диференціали незалежних змінних. Якщо змінення функції позначити dF, а змінення змінних dX, використовуючи векторне позначення можемо записати:
– диференціали незалежних змінних. Якщо змінення функції позначити dF, а змінення змінних dX, використовуючи векторне позначення можемо записати: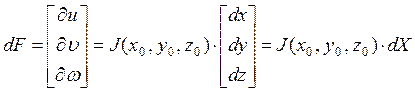 (4.4)
(4.4) (4.5)
(4.5) . Якщо початкова точка достатньо близько розташована до точки
. Якщо початкова точка достатньо близько розташована до точки  (4.6)
(4.6)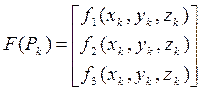 (4.7)
(4.7)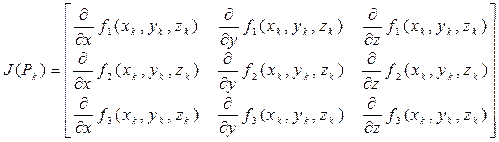 (4.8)
(4.8)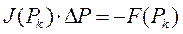
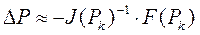
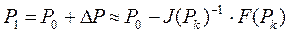 (4.9)
(4.9)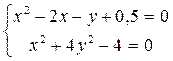
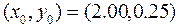 .
.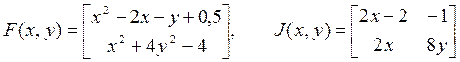 .
.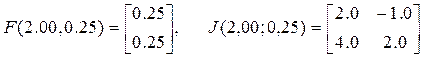 .
.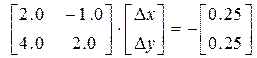
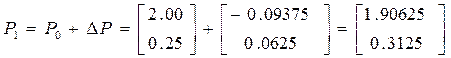

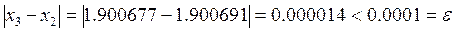 .
.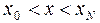 , її значення називають інтерполяційним, якщо за межами інтервалу
, її значення називають інтерполяційним, якщо за межами інтервалу 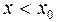 чи
чи 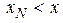 – екстраполяційними. Так побудова поліному для знаходження проміжних точок називається інтерполяцією, для знаходження значень за межами заданого інтервалу – екстраполяцією. Широке застосування наближуючі поліноми знаходять також у чисельному диференціюванні, чисельному інтегруванні, розв‘язанні нелінійних рівнянь та обробці графічних зображень. Наближення реальної функції деякою простішою функцією називається апроксимацією.
– екстраполяційними. Так побудова поліному для знаходження проміжних точок називається інтерполяцією, для знаходження значень за межами заданого інтервалу – екстраполяцією. Широке застосування наближуючі поліноми знаходять також у чисельному диференціюванні, чисельному інтегруванні, розв‘язанні нелінійних рівнянь та обробці графічних зображень. Наближення реальної функції деякою простішою функцією називається апроксимацією.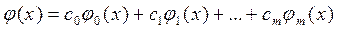 (5.1)
(5.1)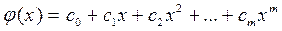 (5.2)
(5.2)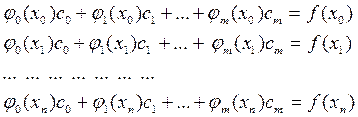 (5.3)
(5.3)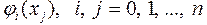 лінійно незалежні. Наведена вище задача називається задачею інтерполяції.
лінійно незалежні. Наведена вище задача називається задачею інтерполяції. (5.4)
(5.4)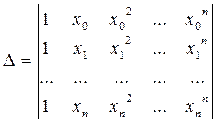 , (5.5)
, (5.5)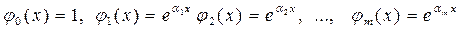 (5.6)
(5.6)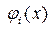 – деяка числова послідовність попарно різних дійсних чисел. У такому випадку інтерполяційний поліном запишемо у вигляді:
– деяка числова послідовність попарно різних дійсних чисел. У такому випадку інтерполяційний поліном запишемо у вигляді: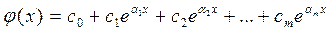 . (5.7)
. (5.7)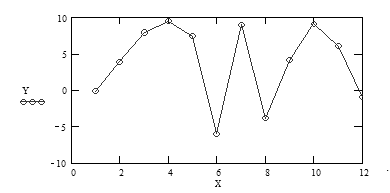
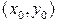 ,
, 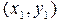 дорівнює
дорівнює 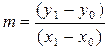 . Для точки у, що належить проміжку
. Для точки у, що належить проміжку 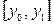 , можемо записати:
, можемо записати: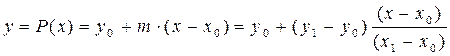 (5.8)
(5.8)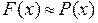 . При класичному розв‘язуванні задачі вимагається також строгий збіг значень
. При класичному розв‘язуванні задачі вимагається також строгий збіг значень 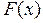 та
та  у вузлах інтерполяції
у вузлах інтерполяції 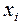 .
.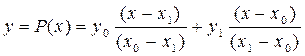 (5.9)
(5.9)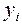 називаються коефіцієнтами Лагранжа. Побудуємо коефіцієнти Лагранжа для n точок. Особливість їх побудови полягає у виключенні з ряду різниць, що перемножуються у чисельнику і знаменнику, різниці зі значенням
називаються коефіцієнтами Лагранжа. Побудуємо коефіцієнти Лагранжа для n точок. Особливість їх побудови полягає у виключенні з ряду різниць, що перемножуються у чисельнику і знаменнику, різниці зі значенням 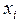 після знаку “–”. Для n точок коефіцієнт Лагранжа запишемо у загальному вигляді так:
після знаку “–”. Для n точок коефіцієнт Лагранжа запишемо у загальному вигляді так: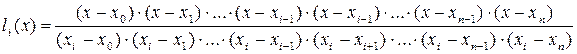 (5.10)
(5.10)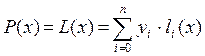 (5.11)
(5.11)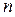 порядок поліному збільшується відповідно до ступеню (
порядок поліному збільшується відповідно до ступеню (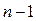 ).
).
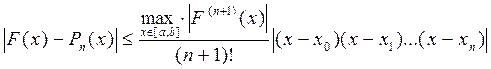 (5.12)
(5.12)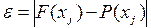 де j – номери точок, які не є вузловими. У вузлових точках функція помилки за визначенням має значення нуль
де j – номери точок, які не є вузловими. У вузлових точках функція помилки за визначенням має значення нуль 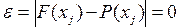 .
.


