ЧИСЛЕННЫЕ МЕТОДЫ
ЧИСЛЕННЫЕ МЕТОДЫ
Вычислительная математика – наука, которая изучает методы построения и исследования численных методов решения задач, моделирующих различные процессы, явления. Численные методы – методы приближенного решения задач, основанные на построении конечной последовательности действий над конечным множеством действий. Этапы построения задач на ЭВМ: 1) Постановка задачи. На этом этапе формулируются условие задачи, математические термины или предпосылки. Далее определяется, что нужно найти и в каком виде представляется результат. 2) Построение математической модели. Модель – упрощенное по сравнению с реальностью описание объекта, явления, процесса. При этом учитываются только существенные с точки зрения исследователя свойства этого процесса. Модели бывают: математические, химические, физические и т.д.. Математическая модель – модель, которая сформулирована математически. Требования к математической модели: – требование простоты; – адекватности; 3) Выбор полученной системы уравнений. 4) Разработка алгоритма решения полученной задачи (определение последовательности действий для достижения указанной цели). 5) написание алгоритма на языке какого-либо высокого уровня и отладка программы. Тестирование задачи – решение задачи, которое уже известно, с некоторым набором исходных данных. 6) Получение решения задачи. 7) Анализ полученного решения.
МЕТОДИКА ОЦЕНКИ ПОГРЕШНОСТИ Полная погрешность вычислительного процесса такова: Приближение числа. Погрешности. Приближенным значением числа a называется число, незначительно отличающееся от точного значения числа x и заменяющее последнее в вычислениях. Разница между двумя этими числами называется а бсолютной погрешностью числа и обозначается Например.
Найдем по графику функции если x=1, 5, то y По формуле если x=1, 5, то Найдем абсолютную погрешность:
Относительной погрешностью числа называется отношение абсолютной погрешности и его точного значения, но т.к. точное значение числа неизвестно, то его заменяют приближенным значением. Выражается в процентах.
Например. Округлим дробь 14, 7 до целых и найдем относительную погрешность приближенного значения:
Поскольку в расчетах оперирую только предельными значениями погрешностей, то принято называть их просто абсолютной и относительной погрешностями. Запись приближенных чисел. Принято записывать приближенные числа так, чтобы в записи числа были только верные (в строгом смысле) цифры. Все сомнительные цифры отбрасываются по правилам округления, тогда по форме записи числа можно судить о его погрешности. Различают цифры верные в широком и строгом смыслах. Верной цифрой в широком смысле приближенного значения называют цифру любого разряда, если абсолютная погрешность не превосходит единицы этого разряда, в котором находится данная цифра.
Проверим цифру 7. Единица ее разряда 10> 0, 05. Значит она верная. Цифра 3: 1> 0, 05 – тоже верная. Аналогично верными будут и цифры 6 и 4: 0, 1> 0, 05, 0, 01> 0, 05, а вот цифра 2 будет сомнительной. Действительно, для 2: 0, 001< 0, 05. Верной цифрой в строгом смысле приближенного значения называют цифру любого разряда, если абсолютная погрешность не превосходит половины разряда, в котором находится данная цифра.
Проверим цифру 7. Половина единицы ее разряда Оценка погрешности значений элементарных функций: – абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме абсолютных погрешностей этих чисел; – относительная погрешность произведения и частного нескольких приближенных чисел, отличных от нуля, равна сумме относительных погрешностей этих чисел. Основные приемы приближенных вычислений: – вычисления со строгим учетом погрешности (по правилам, описанным ранее); – вычисления без строгого учета погрешности. Вычисления производятся при сохранении в промежуточном результате на одну цифру больше, чем имеет их число с наименьшим количеством значащих цифр.В окончательном результате эта цифра отбрасывается. Значащими называются все цифры, начиная с первой (слева), отличной от нуля. Например.
Понятия устойчивости, корректности, сходимости Устойчивость – чувствительность задачи к исходным данным. Задача называется устойчивой по исходному параметру x, если решение непрерывно от него зависит. Задача называется поставленной корректно, если для любого значения исходных данных из некоторого класса ее решение существует, оно единственно и устойчиво по исходным данным. Сходимость – близость численного решения задачи к истинному. Различают сходимость итерационных методов и дискретных методов.
РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ Будем рассматривать уравнения вида f(x)=0 с изолированными корнями. Теорема о существовании корня (теорема Коши): если функция f(x) непрерывна и дифференцируема и имеет разные значения на концах этого отрезка, то внутри этого отрезка существует корень и он может быть не один. Теорема о существовании и единственности корня (теорема Коши): если функция f(x) непрерывна и дифференцируема и имеет разные значения на концах этого отрезка, а первая и вторая производные сохраняют знак на этом отрезке, то внутри этого отрезка существует корень и он единственный. Решение уравнения складывается из двух этапов: 1) отделение (изолирование) корней; 2) уточнение значения корней. Изолировать корни можно: – аналитически. Для этого табулируем функцию на некотором отрезке. Табулирование функции – это вычисление значений функции при изменении аргумента от некоторого начального значения до некоторого конечного значения с определённым шагом. Именно так составляются таблицы значений функций, отсюда и название – табулирование.
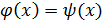 и строят графики функций y1= и строят графики функций y1=  и y2= и y2=  Абсциссы точек пересечения этих графиков дают приближенные значения искомых корней. Абсциссы точек пересечения этих графиков дают приближенные значения искомых корней.
Существуют разные методы уточнения приближенных значений корней, т.е. доведение их до заданной точности. Рассмотрим некоторые из них. Итерационные методы. Рассмотрим общие принципы решения уравнений итерационными методами. Дано уравнение f(x)=0 с изолированным корнем Различают следующие методы решения:
Итерационную последовательность продолжают до тех пор, пока результаты двух последних итераций не станут близкими, т.е. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ Рассмотрим произвольную систему m – линейных уравнений с n – неизвестными:
где Все методы решения систем линейных уравнений можно условно разбить на точные (прямые) и приближенные. К точным алгоритмам относят методы Крамера, Гаусса и т.д. Среди приближенных следует отметить прежде всего итерационные методы. Гауссовы преобразования. Рассмотрим два любых уравнения системы, выписав коэффициенты при неизвестных xp и xj в строках q и i: xp … xj q … aqp … aqj i … aip ... aij Преобразуем уравнение q так, чтобы коэффициент при xp был равен 1, тогда коэффициенты при остальных переменных в этой строке будут равны: a'qp Преобразование матриц по этим формулам называется гауссовым, aqp – разрешающим элементом, строка q – разрешающей строкой, столбец p – разрешающим столбцом. Из литературы широко известен метод Гаусса в различных модификациях: – метод Гаусса по схеме единственного деления. Его сущность заключается в том, что с помощью гауссовых преобразований исходную матрицу коэффициентов системы приводят к треугольному виду (прямой ход), а затем находят неизвестные (обратный ход метода). – метод Гаусса с выбором главного элемента. Его сущность заключается в том, что за разрешающий выбирают любой элемент, а затем с помощью гауссовых преобразований исходную матрицу коэффициентов системы приводят к единичному базису. При этом значения неизвестных – значения свободных членов матрицы. Нахождение обратной матрицы. Дана неособенная (невырожденная) матрица A =[ aij ]. Матрица называется невырожденной (неособенной), если ее определитель отличен от нуля. Требуется найти обратную матрицу A-1. Матрица A-1 =[ xij ] является обратной данной, если выполняется условие AA-1 = E, где E – единичная матрица. В результате перемножения матриц получим n систем n уравнений с n неизвестными: Метод квадратных корней. Применяется для систем, имеющих симметрические матрицы коэффициентов. Квадратная матрица называется симметрической, если
Подставим А = Т'Т в уравнение АХ=В, получим Т'Т Х=В. Обозначив Т Х через Y, Т' Y =В. получим Решение системы линейных уравнений АХ=В сводится к решению двух систем линейных уравнений: Т Х=Y и Т' Y =В. Из решения двух этих систем последовательно найдем:
Решение систем линейных уравнений методом итерации. Пусть дана система линейных уравнений АХ=В. Предполагая, что диагональные коэффициенты Достаточным условием итерационной последовательности является выполнение одного из условий: Метод Зейделя. Представляет собой некоторую модификацию метода итерации. Основная идея заключается в том, что при вычислении k-го порядка приближения неизвестной хi неизвестные х1, х2, …., хi-1. Обычно метод Зейделя дает лучшую сходимость, чем метод простой итерации. ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ ПОЛИНОМАМИ Рассмотрим некоторую функцию y=f(x) непрерывна на отрезке [a; b]. Эта функция может иметь сложный вид, что может затруднить обработку, либо она может быть задана своими значениями Постановка задачи. Требуется исходную функцию приближенно заменить (аппроксимировать) некоторой другой функцией Постановка задачи интерполирования. Дана функция y=f(x) на отрезке [a; b]. Пусть в точках Интерполирование – частный случай аппроксимации. Интерполяционный полином Лагранжа. Пусть функция y=f(x) задана на отрезке [a; b]. Разобьем отрезок точками
где
Например для случая линейной интерполяции
для случая квадратичной интерполяции
Оценка погрешности.
Интерполяционные полиномы Ньютона. Применяются при равномерном разбиении. Конечные разности. Пусть функция y=f(x) задана на отрезке [a; b]. Разобьем отрезок точками

…

…
и т.д. Конечные разности более высокого порядка можно выразить через функции. Например:
Порядок конечных разностей не превышает порядка исходного многочлена. Следствие. Чтобы определить порядок строящегося полинома необходимо построить таблицу конечных разностей и определить их наивысший порядок. Первая Интерполяционная формула Ньютона (формула Ньютона для интерполирования вперед). Постановка задачи. Пусть функция y=f(x) задана на отрезке [a; b]. Разобьем отрезок точками
…
Обозначим через
Например для случая линейной интерполяции
для случая квадратичной интерполяции
Оценка погрешности.
Вторая интерполяционная формула Ньютона (формула Ньютона для интерполирования назад). Постановка задачи. Пусть функция y=f(x) задана на отрезке [a; b]. Разобьем отрезок точками
вторая интерполяционная формула Ньютона (формула Ньютона для интерполирования назад). Оценка погрешности.
ОБРАТНОЕ ИНТЕРПОЛИРОВАНИЕ Задача обратного интерполирования заключается в том, чтобы по заданному значению функции f(x) определить соответствующее значение аргумента. Если известно, что f(x) определена, монотонна и непрерывна в заданном промежутке, то в соответствующем промежутке значений функции f(x) существует однозначная обратная функция x=g(y), также монотонная и непрерывная по теореме об обратной функции. Если допустимаинтерполяция по переменной y, то обратную функцию x=g(y) можно заменить интерполяционным многочленом
При равномерном разбиении отрезка применяют интерполяционный многочлен Ньютона:
отсюда
Решение уравнения f(x)=0 можно свести к задаче обратного интерполирования. Для этого нужно составить таблицу значений функции y=f(x) на отрезке [ a; b ], построить соответствующую таблицу конечных разностей и определить порядок старшего полинома Ньютона. Затем применить приемы обратного интерполирования, отыскивая значение x, соответствующее y=0.
ПРИБЛИЖЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ Пусть дана функция y=f(x) на отрезке [a; b], которая имеетсложный видили задана таблично. Дифференцировать функцию в этих случаях будет затруднительно. Поэтому ее заменяют некоторой другой функцией Разобьем отрезок [a; b] точками
Аналогично можно найти и производные более высоких порядков. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ Если функция f(x) непрерывна на отрезке [a; b] и известна первообразная F(x), то определенный интеграл от функции f(x) в заданных пределах может быть вычислен по формуле Ньютона-Лейбница:
Однако, во многих случаях первообразная F(x) не может быть представлена в виде элементарной функции. Кроме того, на практике функция f(x) часто задается таблично и тогда само понятие первообразной теряет смысл. В этих случаях используются методы численного интегрирования. Они основаны на аппроксимации функции f(x) некоторыми более простыми выражениями, например, многочленами. Метод трапеции. Пусть дана функция f(x) непрерывна на отрезке [a; b] и известна ее первообразная F(x). Требуется вычислить определенный интеграл функции f(x) в заданных пределах: Разобьем отрезок [a; b] точками Рассмотрим интеграл Аналогично находим Складывая полученные интегралы, получим:
Погрешность метода вычисляется по формуле:
Метод Симпсона. Пусть дана функция f(x) непрерывна на отрезке [a; b] и известна ее первообразная F(x). Требуется вычислить определенный интеграл функции f(x) в заданных пределах: Разобьем отрезок [a; b] на четное количество отрезков точками Рассмотрим интеграл Аналогично находим Складывая полученные интегралы, получим:
Погрешность метода вычисляется по формуле:
ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ Пусть некоторая функция получена в результате проведения эксперимента. Задача состоит в том, чтобы найти приближенную зависимость y=f(x), значения которой при x=xi мало отличаются от опытных данных yi. Полученная приближенная функциональная зависимость называется эмпирической формулой. Этапы построения эмпирической формулы: 1) подбор общего вида формулы; 2) определение параметров формулы. Способы подбора параметров эмпирической формулы могут быть разными, но наиболее широко используется метод наименьших квадратов. Метод наименьших квадратов. Параметры эмпирической формулы подбирают исходя из условия минимума суммы квадратов отклонений Обозначим через
где Решая системы уравнений, определим параметры эмпирической формулы.
|

 . Погрешность входных данных и математической модел и
. Погрешность входных данных и математической модел и  – это неустранимая погрешность, поскольку, во-первых, реально протекающие процессы достаточно трудно описать математически, во-вторых, это связано с неточностью задания исходных параметров. Погрешность метода
– это неустранимая погрешность, поскольку, во-первых, реально протекающие процессы достаточно трудно описать математически, во-вторых, это связано с неточностью задания исходных параметров. Погрешность метода  – это погрешность, в результате замены одного математического процесса другим. Это – регулируемая погрешность, т.к. можно выбрать боле или менее точный метод расчета. Погрешность округления
– это погрешность, в результате замены одного математического процесса другим. Это – регулируемая погрешность, т.к. можно выбрать боле или менее точный метод расчета. Погрешность округления  связана с округлением данных в процессе вычислений.
связана с округлением данных в процессе вычислений. .
.
 ее приближенное значение при x=1, 5:
ее приближенное значение при x=1, 5: 2, 3.
2, 3. .
.


 %.
%.
 Предельной абсолютной погрешностью называется всякое число, не меньшее абсолютной погрешности этого числа, т.е. предельная абсолютная погрешность показывает в каких границах изменяется точное значение числа:.
Предельной абсолютной погрешностью называется всякое число, не меньшее абсолютной погрешности этого числа, т.е. предельная абсолютная погрешность показывает в каких границах изменяется точное значение числа:. Предельной относительной погрешностью называется всякое число, не меньшее относительной погрешности этого числа
Предельной относительной погрешностью называется всякое число, не меньшее относительной погрешности этого числа Например.
Например.
 > 0, 05. Значит она верная. Цифра 3:
> 0, 05. Значит она верная. Цифра 3:  > 0, 05 – тоже верная. Аналогично верной будет и цифры 6:
> 0, 05 – тоже верная. Аналогично верной будет и цифры 6:  0, 05, а вот цифры 4 и 2 будут сомнительными. Действительно, для 4: 0, 005< 0, 05, 2: 0, 0005< 0, 05.
0, 05, а вот цифры 4 и 2 будут сомнительными. Действительно, для 4: 0, 005< 0, 05, 2: 0, 0005< 0, 05. – (3) значащие цифры;
– (3) значащие цифры; – (3) значащие цифры;
– (3) значащие цифры; – (4) значащие цифры.
– (4) значащие цифры. – корень уравнения, если после подстановки, мы получаем f(
– корень уравнения, если после подстановки, мы получаем f(  )=0. Корень
)=0. Корень  [a; b]. Преобразуем уравнение к виду
[a; b]. Преобразуем уравнение к виду  . Итерационный процесс состоит в последовательном уточнении начального приближении
. Итерационный процесс состоит в последовательном уточнении начального приближении  :
:  Каждый такой шаг называется итерацией. В результате итераций находим последовательность приближенных значений корня
Каждый такой шаг называется итерацией. В результате итераций находим последовательность приближенных значений корня 
 . Методы, основанные на построении итерационной последовательности, называются итерационными.
. Методы, основанные на построении итерационной последовательности, называются итерационными.


 ,
, 



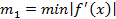


 координаты неподвижного конца отрезка
координаты неподвижного конца отрезка
 , где
, где  – заданная точность приближения.
– заданная точность приближения.
 – неизвестные переменные,
– неизвестные переменные,  – коэффициенты при неизвестных,
– коэффициенты при неизвестных,  – свободные члены системы.
– свободные члены системы. (
( , путем перестановки уравнений всегда можно добиться этого условия). Исключим xp из уравнения i, определив коэффициенты как a'ij
, путем перестановки уравнений всегда можно добиться этого условия). Исключим xp из уравнения i, определив коэффициенты как a'ij 
 , где
, где  символ Кронекера. Чтобы найти A-1 =[ xij ], необходимо решить эти системы уравнений. У всех этих систем одинаковые матрицы коэффициентов, разные только столбцы свободных членов. Это дает нам возможность решать все системы одновременно по схеме единственного деления.
символ Кронекера. Чтобы найти A-1 =[ xij ], необходимо решить эти системы уравнений. У всех этих систем одинаковые матрицы коэффициентов, разные только столбцы свободных членов. Это дает нам возможность решать все системы одновременно по схеме единственного деления. , то есть если равны элементы матрицы, симметричные относительно главной диагонали. Пусть дана линейная система уравнений АХ=В, где A =[ aij ] – симметрическая матрица. Тогда матрицу А можно представить в виде произведения двух транспонированных между собой треугольных матриц А = Т'Т, где Т' – нижняя треугольная матрица, Т – верхняя треугольная матрица. Матрица, в которой строки матрицы А являются столбцами называется транспонированной по отношению к матрице А. Отсюда найдем коэффициенты матрицы Т:
, то есть если равны элементы матрицы, симметричные относительно главной диагонали. Пусть дана линейная система уравнений АХ=В, где A =[ aij ] – симметрическая матрица. Тогда матрицу А можно представить в виде произведения двух транспонированных между собой треугольных матриц А = Т'Т, где Т' – нижняя треугольная матрица, Т – верхняя треугольная матрица. Матрица, в которой строки матрицы А являются столбцами называется транспонированной по отношению к матрице А. Отсюда найдем коэффициенты матрицы Т:



 , преобразуем систему к виду Х=В+АХ. Полученную систему будем решать методом последовательных приближений. За нулевое приближение примем столбец свободных членов
, преобразуем систему к виду Х=В+АХ. Полученную систему будем решать методом последовательных приближений. За нулевое приближение примем столбец свободных членов  . Подставляем значение неизвестного в правую часть уравнения
. Подставляем значение неизвестного в правую часть уравнения  Полученное значение неизвестного снова подставляем в правую часть уравнения
Полученное значение неизвестного снова подставляем в правую часть уравнения  и так далее продолжаем процесс
и так далее продолжаем процесс 

 , т.е. для успешного применения метода итерации модули диагональных коэффициентов системы должны быть велики по сравнению с модулями других коэффициентов.
, т.е. для успешного применения метода итерации модули диагональных коэффициентов системы должны быть велики по сравнению с модулями других коэффициентов. в точках
в точках  . В этом случае отсутствие аналитического выражения функции также не позволит использовать ее в расчетах.
. В этом случае отсутствие аналитического выражения функции также не позволит использовать ее в расчетах. так, чтобы отклонения между ними
так, чтобы отклонения между ними  в точках
в точках  было бы в некотором смысле наименьшим. Функцию
было бы в некотором смысле наименьшим. Функцию 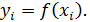 Требуется подобрать полином (многочлен)
Требуется подобрать полином (многочлен)  . Тогда функция
. Тогда функция  узлами интерполирования.
узлами интерполирования. Требуется подобрать полином
Требуется подобрать полином 
 многочлены
многочлены
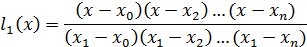


 нтерполяционный полином Лагранжа.
нтерполяционный полином Лагранжа.

 , где
, где  при
при 
 с постоянным шагом
с постоянным шагом  .
.



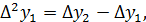

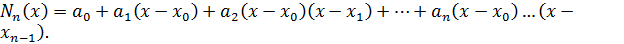

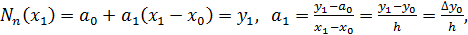

 ,
,

 , откуда
, откуда 
 первая Интерполяционная формула Ньютона (формула Ньютона для интерполирования вперед).
первая Интерполяционная формула Ньютона (формула Ньютона для интерполирования вперед).

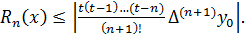
 Обозначим через
Обозначим через  , откуда
, откуда 


 , удовлетворяющим условиям:
, удовлетворяющим условиям:  При использовании интерполяционного полинома Лагранжа последний примет вид:
При использовании интерполяционного полинома Лагранжа последний примет вид:

 , где
, где
 нелинейное уравнение относительно переменной t, которое можно решить методом простой итерации. За начальное приближение примем:
нелинейное уравнение относительно переменной t, которое можно решить методом простой итерации. За начальное приближение примем:  Тогда, применяя метод итерации, получим
Тогда, применяя метод итерации, получим 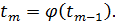 Зная, что
Зная, что 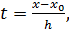 можно найти
можно найти  ,
,  т.д.
т.д.
 Преобразуем выражение, раскрыв скобки:
Преобразуем выражение, раскрыв скобки:  Тогда производная функции будет равна:
Тогда производная функции будет равна:  Откуда
Откуда 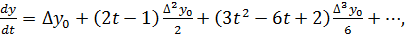
 Подставим полученные выражения, получим:
Подставим полученные выражения, получим:

 .
.

 . Заменим подынтегральную функцию линейным полиномом Ньютона:
. Заменим подынтегральную функцию линейным полиномом Ньютона:  Зная, что
Зная, что  Исходя из того, что
Исходя из того, что  , найдем
, найдем  Получим:
Получим: 


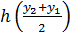 и т.д.
и т.д.
 .
.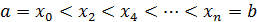 с постоянным шагом
с постоянным шагом 
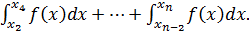
 . Заменим подынтегральную функцию квадратичным полиномом Ньютона:
. Заменим подынтегральную функцию квадратичным полиномом Ньютона:  Зная, что
Зная, что  Исходя из того, что
Исходя из того, что 
 и т.д.
и т.д.
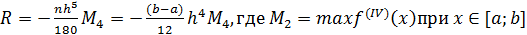 .
. , где
, где 
 . Чтобы определить параметры, необходимо найти частные производные от
. Чтобы определить параметры, необходимо найти частные производные от  по каждому параметру и приравнять их к нулю:
по каждому параметру и приравнять их к нулю:  В итоге получим систему m +1 уравнений:
В итоге получим систему m +1 уравнений:
 при
при 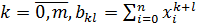 при
при 



