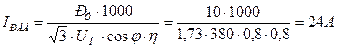Л ТЕЫЕОЙА ЪБДБЮЙ №7
йУИПДОЩНЙ ДБООЩНЙ ДМС ТБУЮЕФБ ЬМЕЛФТЙЮЕУЛЙИ ОБЗТХЪПЛ СЧМСАФУС ХУФБОПЧМЕООБС НПЭОПУФШ ЬМЕЛФТПРТЙЕНОЙЛПЧ Й ИБТБЛФЕТ ЙЪНЕОЕОЙС ОБЗТХЪЛЙ. ч ТЕЪХМШФБФЕ ТБУЮЕФБ ПРТЕДЕМСЕФУС БЛФЙЧОБС, ТЕБЛФЙЧОБС Й РПМОБС НПЭОПУФШ ЬМЕЛФТПРТЙЕНОЙЛПЧ, ЛПФПТБС УМХЦЙФ ПУОПЧПК ДМС ЧЩВПТБ УЕЮЕОЙС РЙФБАЭЙИ РТПЧПДПЧ Й ЛБВЕМЕК, РПФЕТЙ ОБРТСЦЕОЙС, ЧЩВПТБ НПЭОПУФЙ УЙМПЧПЗП ФТБОУЖПТНБФПТБ Й ЛПНРЕОУЙТХАЭЙИ ХУФТПКУФЧ. ъОБС ХУФБОПЧМЕООХА НПЭОПУФШ Й ЛПЬЖЖЙГЙЕОФ УРТПУБ ДБООПК ЗТХРРЩ РПФТЕВЙФЕМЕК, НПЦОП ПРТЕДЕМЙФШ ДМС ЛБЦДПЗП ЬМЕЛФТПРТЙЕНОЙЛБ ТБУЮЕФОХА БЛФЙЧОХА НПЭОПУФШ тт РП ЖПТНХМЕ
тт1 = тх1 . лу1 тт2 = тх2 . лу2љљ Й Ф.Д.
ъБФЕН ПРТЕДЕМСЕФУС УХННБТОБС ТБУЮЕФОБС НПЭОПУФШ ДМС ЧУЕИ ЬМЕЛФТПРТЙЕНОЙЛПЧ:
тт∑ = тт1 + тт2 + тт3 + …. [ЛчФ]
тБУЮЕФОБС ТЕБЛФЙЧОБС НПЭОПУФШ ДМС ЛБЦДПЗП ЬМЕЛФТПРТЙЕНОЙЛБ
QP = PP . tgφ, љљ ЗДЕ
љtgφ – ОБИПДЙФУС РП ЪБДБООПК ЧЕМЙЮЙОЕ cosφ, ЗДЕ љљљљљљ cosφ – ЬФП ЛПЬЖЖЙГЙЕОФ НПЭОПУФЙ, ЛПФПТБС РПЛБЪЩЧБЕФ, ЛБЛХА ЮБУФШ ПФ РПМОПК НПЭОПУФЙ УПУФБЧМСЕФ БЛФЙЧОБС НПЭОПУФШ
φ – ХЗПМ УДЧЙЗБ ЖБЪ НЕЦДХ ФПЛПН Й ОБРТСЦЕОЙЕН Ч ГЕРСИ φ ЪБЧЙУЙФ ПФ ИБТБЛФЕТБ ОБЗТХЪЛЙ (ЙОДХЛФЙЧОБС, ЕНЛПУФОБС, БЛФЙЧОБС, УНЕЫБООБС) ъОБЮЕОЙЕ tgφ љ ПРТЕДЕМСЕФУС ЙМЙ РП ФБВМЙГЕ вТБДЙУБ, ЙМЙ ТБУЮЕФОЩН РХФЕН У РПНПЭША ЛБМШЛХМСФПТБ, ЪОБС ЧЕМЙЮЙОХ cosφ. ъБФЕН ОБИПДСФ УХННБТОХА ТЕБЛФЙЧОХА ТБУЮЕФОХА НПЭОПУФШ ЧУЕИ ЬМЕЛФТПРТЙЕНОЙЛПЧ.
Qт∑ љ= QP1 + QP2 + OP3 + … [ЛчбТ]
рПМОБС ТБУЮЕФОБС НПЭОПУФШ УЙМПЧПК ОБЗТХЪЛЙ
рПФТЕВМСЕНЩК ТБУЮЕФОЩК ФПЛ
тБУЮЕФ УЕЮЕОЙС РЙФБАЭЕЗП ЛБВЕМС чЩВПТ УЕЮЕОЙС РТПЧПДОЙЛБ (РТПЧПДБ, ЛБВЕМС) РТПЙЪЧПДЙФУС РП ДПРХУФЙНЩН ФПЛПЧЩН ОБЗТХЪЛБН, Ф.Е. РП ДПРХУФЙНПНХ ФПЛХ Iдпр. Iдпр – ЬФП ФПЛ, ЛПФПТЩК ЧЩДЕТЦЙЧБЕФ РТПЧПД ЙМЙ ЛБВЕМШ ПРТЕДЕМЕООПЗП УЕЮЕОЙС ДМЙФЕМШОПЕ ЧТЕНС, ОЕ РЕТЕЗТЕЧБСУШ. уПУФБЧМЕОЩ ФБВМЙГЩ, Ч ЛПФПТЩИ ХЛБЪБОЩ ЪОБЮЕОЙС ДПРХУФЙНЩИ ФПЛПЧ ДМС ТБЪМЙЮОЩИ НБТПЛ РТПЧПДПЧ Й ЛБВЕМЕК ТБЪМЙЮОЩИ УФБОДБТФОЩИ УЕЮЕОЙК. чЩВПТ УЕЮЕОЙС РТПЧПДОЙЛБ РП ОБЗТЕЧХ УЧПДЙФУС Л УТБЧОЕОЙА ТБУЮЕФОПЗП ФПЛБ IP У ДПРХУФЙНЩН ФБВМЙЮОЩН ЪОБЮЕОЙЕН Iдпр; РТЙ ЧЩВПТЕ ДПМЦОП УПВМАДБФШУС ХУМПЧЙЕ Iдпрљ > IP љљљљљљ рПМШЪХКФЕУШ ФБВМЙГБНЙ № 12, 13, 14, 15 ъОБЮЕОЙЕ ТБУЮЕФОПЗП ФПЛБ ДМС МЙОЙЙ, РЙФБАЭЕК ПФДЕМШОЩК ФТЕИЖБЪОЩК ЬМЕЛФТПДЧЙЗБФЕМШ УФТПЙФЕМШОПЗП НЕИБОЙЪНБ, ПРТЕДЕМСЕФУС РП ЖПТНХМЕ
ЗДЕ то = тх (ЛчФ) л3 – ЛПЬЖЖЙГЙЕОФ ЪБЗТХЪЛЙ, РТЙОСФШ л3 = 0, 9 η д – л.р.д. ДЧЙЗБФЕМС. cosφ – ЕЗП ЛПЬЖЖЙГЙЕОФ НПЭОПУФЙ Uопн – ОПНЙОБМШОПЕ ОБРТСЦЕОЙЕ. тБУЮЕФОБС УЙМБ ФПЛБ ДМС МЙОЙЙ, РЙФБАЭЕК ЬМЕЛФТПРТЙЧПД УФТПЙФЕМШОПК НБЫЙОЩ У НОПЗПДЧЙЗБФЕМШОЩН ЬМЕЛФТПРТЙЧПДПН ОБ РЕТЕНЕООПН ФПЛЕ (УФТПЙФЕМШОЩЕ ЛТБОЩ, ЬЛУЛБЧБФПТЩ Й Ф.Д.) РТЙВМЙЦЕООП ПРТЕДЕМЕОП РП ЖПТНХМЕ
ЗДЕ тх – УХННБТОБС ХУФБОПЧМЕООБС НПЭОПУФШ НОПЗПДЧЙЗБФЕМШОПЗП УФТПЙФЕМШОПЗП НЕИБОЙЪНБ, ЛчФ лу – ЛПЬЖЖЙГЙЕОФ УРТПУБ. еУМЙ НЕИБОЙЪН ЙНЕЕФ: 2-3 ДЧЙЗБФЕМС, ФП лу =0, 9 4 ДЧЙЗБФЕМС, ФП лу =0, 8 5-6 ДЧЙЗБФЕМЕК, ФП лу =0, 7 лу – ХЮЙФЩЧБЕФ ОЕПДОПЧТЕНЕООПУФШ ТБВПФЩ ДЧЙЗБФЕМЕК Й ЙИ ОЕРПМОХА ЪБЗТХЪЛХ. ъБФЕН РП ФБВМЙГЕ ДПРХУФЙНЩИ ФПЛПЧЩИ ОБЗТХЪПЛ ЧЩВТБФШ ФТЕВХЕНХА НБТЛХ Й УЕЮЕОЙЕ ЛБВЕМС ЙМЙ РТПЧПДБ. хУМПЧЙС ЧЩВПТБ: Iдпр > IP.љљљ рПМШЪХКФЕУШ ФБВМЙГБНЙ № 12, 13, 14, 15
рТПЧЕТЛБ ЛБВЕМС (РТПЧПДБ) РП ДПРХУФЙНПК РПФЕТЕ ОБРТСЦЕОЙС пРТЕДЕМСЕФУС ЖБЛФЙЮЕУЛБС РПФЕТС ОБРТСЦЕОЙС
L – ДМЙОБ ЛБВЕМС, Н; SK – УЕЮЕОЙЕ ЛБВЕМС, НН2; γ – ХДЕМШОБС РТПЧПДЙНПУФШ ФПЛПЧЕДХЭЙИ ЦЙМ; љљљљ НЕДШ U – ОБРТСЦЕОЙЕ УЕФЙ. рПФЕТЙ ОБРТСЦЕОЙС Δ U УТБЧОЙЧБЕФУС У ЧЕМЙЮЙОПК ДПРХУФЙНПК РПФЕТЙ ОБРТСЦЕОЙС Δ Uдпр Δ Uдпр > Δ U еУМЙ ХУМПЧЙЕ ОЕ ЧЩРПМОСЕФУС, ФП ЧЩВТБФШ ЛБВЕМШ (РТПЧПД) ВПМШЫЕЗП УЕЮЕОЙС (УФБОДБТФОПЗП) Й РПЧФПТЙФШ РТПЧЕТЛХ.
рТЙНЕТ ТЕЫЕОЙС ЪБДБЮЙ № 7. йУИПДОЩЕ ДБООЩЕ ПВПТХДПЧБОЙС УФТПЙФЕМШОПЗП ПВЯЕЛФБ фБВМЙГБ 7.1
1. пРТЕДЕМЙФШ БЛФЙЧОХА, ТЕБЛФЙЧОХА Й РПМОХА НПЭОПУФШ УФТПЙФЕМШОПЗП ПВЯЕЛФБ НЕФПДПН ЛПЬЖЖЙГЙЕОФБ УРТПУБ РП РЕТЕЮОА, ХЛБЪБООПНХ Ч ФБВМЙГЕ. 2. пРТЕДЕМЙФШ ТБУЮЕФОЩК ФПЛ, РПФТЕВМСЕНЩК ЬМЕЛФТППВПТХДПЧБОЙЕН УФТПКЛЙ. 3. пРТЕДЕМЙФШ УЕЮЕОЙЕ ЫМБОЗПЧПЗП ЛБВЕМС ДМС РЙФБОЙС УФТПЙФЕМШОПЗП НЕИБОЙЪНБ, ПФНЕЮЕООПЗП Ч ФБВМЙГЕ ЙУИПДОЩИ ДБООЩИ ЪЧЕЪДПЮЛПК (*). чЩВПТ РТПЙЪЧЕУФЙ РП ДПРХУФЙНПНХ ФПЛХ. 4. рТПЧЕТЙФШ ЧЩВТБООЩК ЛБВЕМШ РП ДПРХУФЙНПК РПФЕТЕ ОБРТСЦЕОЙС. Δ Uдпр РТЙОСФШ 5% ПФ U опн = 380 ч.
рПТСДПЛ ТБУЮЕФБ 1. пРТЕДЕМСЕФУС ТБУЮЕФОБС БЛФЙЧОБС НПЭОПУФШ РПФТЕВЙФЕМЕК вБЫЕООЩК ЛТБО: љљљљљљљљљљљљљљљљљљљљљ тт1 = тх . лу = 40 . 0, 7 = 28 ЛчФ ыФХЛБФХТОБС УФБОГЙС: љљљљљљљљљљ тт2 = тх . лу = 10 . 0, 85 = 8, 5 ЛчФ нБМСТОБС УФБОГЙС: љљљљљљљљљљљљљљљљ тт3 = тх . лу = 40 . 0, 85 = 34, 0 ЛчФ ьМЕЛФТПРПЗТХЪЮЙЛ ЛЙТРЙЮБ: љ тт4 = тх . лу = 5, 6 . 0, 85 = 4, 8 ЛчФ ыРБЛМЕЧПЮОЩК БЗТЕЗБФ: љљљљљљљ тт5 = тх . лу = 1, 2 . 0, 1 = 0, 12 ЛчФ пУЧЕЭЕОЙЕ ПВЯЕЛФБ: љљљљљљљљљљљљљљ тт6 = тх . лу = 5 . 1 = 5 ЛчФ 2. уХННБТОБС ТБУЮЕФОБС БЛФЙЧОБС НПЭОПУФШ ЧУЕИ ЬМЕЛФТПРТЙЕНОЙЛПЧ тт = тт1 + тт2 + тт3 + тт5 + тт6 = 28 + 8, 5 + 34 + 4, 80, 12 + 5 = 80, 4 ЛчФ 3. пРТЕДЕМСЕФУС ТЕБЛФЙЧОБС ТБУЮЕФОБС НПЭОПУФШ ЬМЕЛФТПРТЙЕНОЙЛПЧ вБЫЕООЩК ЛТБО: љљљљљљљљљљљљљљљљљљљљљ QP1 = PP1 . tgφ = 28 . 1, 02 = 28, 56 ЛчбТ ыФХЛБФХТОБС УФБОГЙС: љљљљљљљљљљ QP2 = PP2 . tgφ = 8, 5 . 0, 75 = 6, 4 ЛчбТ нБМСТОБС УФБОГЙС: љљљљљљљљљљљљљљљљ QP3 = PP3 . tgφ = 34 . 0, 75 = 25, 5 ЛчбТ ьМЕЛФТПРПЗТХЪЮЙЛ ЛЙТРЙЮБ: љ QP4 = PP4 . tgφ = 4, 8 . 0, 48 = 2, 3 ЛчбТ ыРБЛМЕЧПЮОЩК БЗТЕЗБФ: љљљљљљљљ QP5 = тт5 . tgφ = 0, 12 . 1, 02 = 0, 122 ЛчбТ пУЧЕЭЕОЙЕ ПВЯЕЛФБ: љљљљљљљљљљљљљљ QP6 = PP6 . tgφ = 0 ЛчбТ ъОБЮЕОЙЕ tgφ ПРТЕДЕМЙФШ УБНПУФПСФЕМШОП Й ЪБОЕУФЙ Ч ФБВМЙГХ. 4. пРТЕДЕМСЕФУС УХННБТОБС ТЕБЛФЙЧОБС НПЭОПУФШ ЧУЕИ ЬМЕЛФТПРТЙЕНОЙЛПЧ QP = QP1 + QP2 + QP3 + QP4 + QP5 + QP6 = 28, 56 + 6, 4 + 25, 5 + 2, 3 + 0, 122 = 63 ЛчбТ 5.пРТЕДЕМСЕФУС ТБУЮЕФОБС РПМОБС НПЭОПУФШ ЧУЕИ ЬМЕЛФТПРТЙЕНОЙЛПЧ УФТПЙФЕМШОПЗП ПВЯЕЛФБ
6. пРТЕДЕМСЕФУС ТБУЮЕФОЩК ФПЛ РПФТЕВМСЕНЩК ЬМЕЛФТППВПТХДПЧБОЙЕН УФТПЙФЕМШОПК РМПЭБДЛЙ
тЕЪХМШФБФЩ ТБУЮЕФБ ЪБОЕУФЙ Ч ФБВМЙГХ 7.1 7.пРТЕДЕМСЕФУС УЕЮЕОЙЕ ЛБВЕМС ДМС РПДБЮЙ ОБРТСЦЕОЙС Л УФТПЙФЕМШОПНХ НЕИБОЙЪНХ вБЫЕООЩК ЛТБО; УЙМБ ФПЛБ Ч ЛБВЕМЕ, РЙФБАЭЕН ВБЫЕООЩК ЛТБО:
η – л.р.д. рТЙОСФШ Ч РТЕДЕМБИ 0, 7џ0, 8. рП ФБВМЙГЕ № 12, 13, 14, 15љ ЧЩВЙТБЕН ЫМБОЗПЧЩК ЛБВЕМШ НБТЛЙ лтрф (ЙМЙ зты, ЙМЙ ытру) 3-И ЦЙМШОЩК, НЕДОЩК, УЕЮЕОЙЕН SK = 25 НН2, ДМС ЛПФПТПЗП ДПРХУФЙНЩК ФПЛ Iдпр = 105б; 105б > 81б – ХУМПЧЙЕ РП ДПРХУФЙНПНХ ФПЛХ ЧЩРПМОЕОП. 8. рТПЧЕТЛБ ОБ љРПФЕТА ОБРТСЦЕОЙС. пРТЕДЕМСЕФУС ЖБЛФЙЮЕУЛБС РПФЕТС ОБРТСЦЕОЙС Ч ЛБВЕМЕ
ыФХЛБФХТОБС УФБОГЙС
рП ФБВМЙГЕ ЧЩВЙТБЕН УЕЮЕОЙЕ 3-И ЦЙМШОПЗП НЕДОПЗП ЫМБОЗПЧПЗП ЛБВЕМС НБТЛЙ лтрф (ЙМЙ ДТХЗПЗП ЛБВЕМС) Sл = 2, 5 НН2, ДМС ЛПФПТПЗП Iдпр = 28б 28б > 24б – ХУМПЧЙЕ ЧЩРПМОЕОП. пРТЕДЕМСЕФУС ЖБЛФЙЮЕУЛБС РПФЕТС ОБРТСЦЕОЙС Ч ЛБВЕМЕ:
Δ Uж < Δ Uдпр.љљљљљљ Δ Uдпр = 5% бОБМПЗЙЮОП ЧЕУФЙ ТБУЮЕФ ДМС ПУФБМШОЩИ НЕИБОЙЪНПЧ.
фБВМЙГБ 9
|

 : љ
: љ љљљљ [лчб]
љљљљ [лчб] љ [б]
љ [б] љљ [A]
љљ [A]
 љ [%] – ДМС ПДОПДЧЙЗБФЕМШОПЗП НЕИБОЙЪНБ
љ [%] – ДМС ПДОПДЧЙЗБФЕМШОПЗП НЕИБОЙЪНБ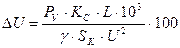 љ[%] – ДМС НОПЗПДЧЙЗБФЕМШОПЗП НЕИБОЙЪНБ
љ[%] – ДМС НОПЗПДЧЙЗБФЕМШОПЗП НЕИБОЙЪНБ ; БМАНЙОЙК
; БМАНЙОЙК 


 љљ
љљ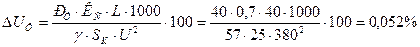 , ЮФП НЕОШЫЕ, ЮЕН 5%. рПФЕТЙ ОБРТСЦЕОЙС НЙОЙНБМШОБС.
, ЮФП НЕОШЫЕ, ЮЕН 5%. рПФЕТЙ ОБРТСЦЕОЙС НЙОЙНБМШОБС.