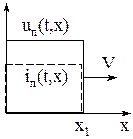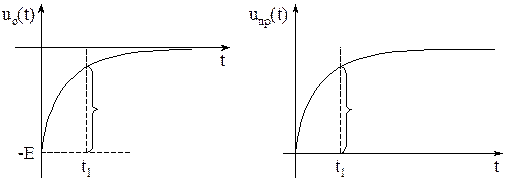Расчет переходных процессов в длинной линии с помощью схемы замещения с сосредоточенными параметрами

 

Расчет переходных процессов в длинной линии с помощью схемы замещения с сосредоточенными параметрами.

 

Процессы в длинной линии.

Решение уравнений линий без потерь: напряжение и ток в длинной линии являются функцией двух переменных t и x.

Решение этой системы в общем случае затруднительно. Для линии без потерь задача решается.

- фазовая скорость

- (*) уравнение колебаний среды.

Решение уравнения (*) в общем случае:

Возникают волны в местах коммутации и неоднородности линии. Форма волны может быть различна.

 

Падающие волны.

Рассмотрим падающие волны при подключении линии к источнику постоянной ЭДС.

 

 

Поскольку линия не имеет потерь и ЭДС постоянна, то при движении падающей волны вдоль линии ее форма не изменится.

Начальный участок волны первым движущийся вдоль линии называется фронтом волны.

 

Пространственно временное распределение падающей волны в линии для данного примера можно записать в виде:

Каков бы ни был закон изменения напряжения в начале линии, по тому же закону будет изменяться напряжение в любой точке х в линии, но с запозданием во времен равном х/v(обусловленным конечной скоростью распространения волн вдоль линии).

Общее правило: если известно аналитическое выражение для тока и напряжения в той точке линии откуда волна начинает свое перемещение, то для получения закона изменения этих величин функции t и x в исходном выражении заменить t→ (t-x/v) и координату х отсчитывать в сторону направления движения волны. Результаты необходимо умножить на единичную ступенчатую функцию 1(t-x/v).

 

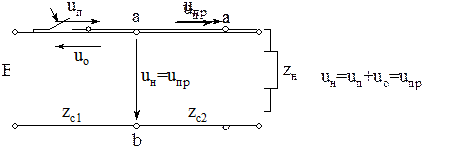
Отраженные и преломленные волны.

Если на пути волны встречается неоднородность, то происходит отражение волны. В зависимости от характера неоднородности отражение может быть полным или частичным. В случае частичного отражения наряду с отраженной волной возникает преломленная волна, распространенная с места нарушения однородности. В случае полного отражения преломленная волна отсутствует. Полное отражение имеет место в конце линии, частичное – в местах стыка линии.

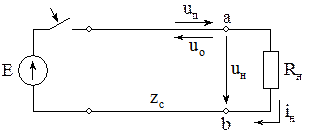
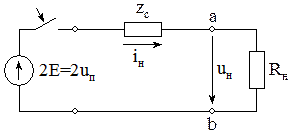
Расчет отраженных и преломленных волн с помощью СЗ с распределенными параметрами.

 

Переходный процесс полученной цепи рассчитывается известными методами. В результате расчета необходимо определить U_н(t).

 

Пространственно-временное распределение отраженной волны с учетом вышеизложенного правила

1.В какой точке возникает отраженная волна (от нагрузки).

2.Спустя какое время от момента замыкания ключа возникает отраженная волна. Отраженная волна в данном примере возникает в линии через интервал ∆ t от момента замыкания ключа.

 

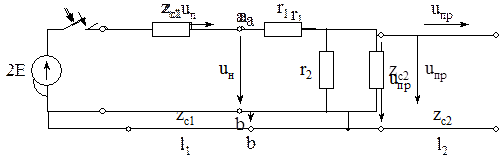
Случай частного отражения

 

 

На рисунке графики напряжений отраженной и прямой волн в месте стыка линий.

 

Графики распределения напряжения вдоль линий для некоторого промежуточного момента времени t₁.

 

Закон пространственно- временного распределения напряжения отраженной и прямой волн.

 

Расчет отраженных и преломленных волн с помощью коэффициента отражения.

 

 

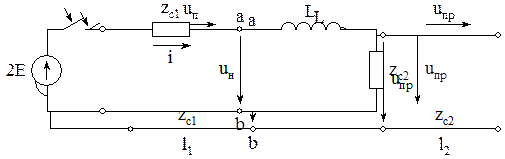
При наличии в схеме реактивных элементов расчет может быть произведен с помощью операторного коэффициента отражения.

 

Нарисуем графики U₀(t) и U_пр(t) в месте стыка линий для емкостного случая:

 

Нарисуем распределение напряжения в линии для момента времени t₁.

Закон пространственно-временного распределения напряжения в линии:

 

Диаграмма движения волн.

Позволяет оценить количество волн в линии в заданный момент времени.

К моменту t₁ в линии имеют место падающие волны напряжения и тока

U_п1и i_п1, и отраженные от нагрузки волны U_о1и i_о1. Фронт отраженной волны подошел к точке (а).

Результирующие напряжение и ток в линии.

Когда обратные волны подойдут к источнику ЭДС возникают вторичные падающие волны в результате отражения от источника. Т.к. внутренне сопротивление идеального источника ЭДС равно нулю, то коэффициент отражения от источника

В момент t₂ фронт вторичных падающих волн находится в точке (в), а напряжение и ток в линии.