Повторитель напряжения на основе ОУ
Схема повторителя (рис. 10.4) легко может быть получена из схемы неинвертирующего усилителя при R1 →
Рис. 10.4. Повторитель напряжения на основе ОУ
Сумматор напряжения (инвертирующий сумматор) Рассмотрим схему сумматора, приведенную на рис. 10.5.
Рис. 10.5. Сумматор напряжения (инвертирующий сумматор) Предположим, что операционный усилитель работает в режиме усиления, тогда uдиф
Для уменьшения влияния входных токов ОУ в цепь неинвертирующего входа включают резистор с сопротивлением Rэ = R1 // R2 //… // Rn // Rос .
Вычитающий усилитель (усилитель с дифференциальным входом) В вычитающем усилителе (рис. 10.6) один входной сигнал подается на инвертирующий вход, а второй – на неинвертирующий.
Рис. 10.6. Вычислительный усилитель с дифференциальным входом
Предположим, что ОУ работает в линейном режиме. Тогда все устройство можно считать линейным и для анализа принцип суперпозиции (наложения). Если uвх2 = 0, тогда соответствующее выходное напряжение u'вых будет определяться выражением, соответствующим инвертирующему усилителю:
Если uвх1 = 0, определим напряжение на выходе u''вых. Для оценки воздействия напряжения uвх2 целесообразно на основе теоремы об эквивалентном генераторе преобразование цепи, подключенной к неинвертирующему входу (рис. 10.7). Как следует из теоремы,
Рис. 10.7 В соответствии с принципом суперпозиции, общее напряжение на выходе uвых определяется из выражения
при R1 = R2 = R3 = R4
|

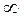 , R2 → 0. Здесь предполагается, что операционный усилитель работает в режиме усиления (uдиф
, R2 → 0. Здесь предполагается, что операционный усилитель работает в режиме усиления (uдиф  0). Используя второй закон Кирхгофа, получаем uвых = uвх.
0). Используя второй закон Кирхгофа, получаем uвых = uвх.

 . При uдиф
. При uдиф  .
.
 .
. ,
, 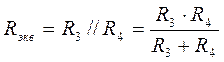 .
.
 ,
, .
.


