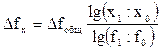Методы измерения влияния факторов в детерминированном анализе

В основе методов, используемых при измерении влиянии факторов в детерминированном анализе, лежит элиминирование.

Элиминирование – есть приём, при котором последовательно выделяется влияние одного фактора и исключается действия всех остальных.

В детерминированном факторном анализе используются следующие методы:

1. Метод цепной подстановки – позволяет определить влияние отдельных факторов на изменение величины результативного показателя путём постепенной замены базисной величины каждого факторного показателя в объёме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, 3-х и последующих факторов, допуская, что остальные не меняются.

Рассмотри этот метод на примере модели, отражающей сумму, получаемых процентов по облигациям:

П=К*Р*СП,

где К – количество облигаций, Р – стоимость облигации, СП – уровень процентной ставки.

П₀=К₀*Р₀*СП₀ – базовый вариант;

П_усл1= К₁*Р₀*СП₀

П_усл2=К₁*Р₁*СП₀

П₁= К₁*Р₁*СП₁

∆ П_к=П_УСЛ1-П₀

∆ П_Р=П_УСЛ2-П_УСЛ1

∆ П_СП=П₁-П_УСЛ2

∆ П_ОБЩ=Пк+Пр+Псп=П₁-П₀

2. Метод абсолютных разниц, заключается в том, что величина влияния факторов рассчитывается умножение абсолютного прироста значения, исследуемого фактора, на базовой уровень факторов, который находится справа от него, и на текущий уровень факторов, расположенный слева от него в модели:

Δ Пк=Δ К*По*СПо

Δ Пр=К₁*Δ Р*СПо

Δ Псп=К₁*П₁*Δ СП

3. Метод относительных разниц, заключается в том, что для расчета влияния первого фактора, необходимо базовую величину результативного показателя умножить на относительный прирост 1-го фактора, выраженном в виде десятичной дроби. Чтобы рассчитать влияние 2-го фактора, нужно к базовой величине результативного показателя прибавить изменение его за счёт 1-го фактора и затем полученную сумму умножить на относительный прирост 2-го фактора и т.д.

∆ Пк=П₀*(∆ К/К₀)

∆ Пр=(П₀+∆ Пк)*(∆ Р/Р₀)

∆ Псп=(П₀+∆ Пк+∆ Пр)* (∆ СП/СП₀).

 

4. Метод пропорционального деления рассмотрим на примере следующей модели:

Y=a+b+c

∆ Ya=(∆ Yобщ/(∆ a+∆ b+∆ c))*∆ a

∆ Yb=(∆ Yобщ/(∆ a+∆ b+∆ c))*∆ b

∆ Yc=(∆ Yобщ/(∆ a+∆ b+∆ c))*∆ c

5. Интегральный метод:

f=x*y

∆ fx=∆ x*y₀+1/2∆ x*∆ y=1/2*∆ x(y₀+y₁)

∆ fy=∆ y*x₀+1/2*∆ x*∆ y=1/2*∆ y*(x₀+x₁)

6. Метод логарифмирования – общий прирост результативного показателя распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму индекса результативного показателя:

f=xyz

Сфера применения методов детерминированного факторного анализа к решению моделей разного типа в систематизированном виде можно представит в виде следующей матрицы:

Метод	Модели
мультипликативная	аддитивная	кратная	Смешанная
Цепной подстановки	+	+	+	+
Абсолютных разниц	+	-	-	Y=a(b-c)
Относительных разниц	+	-	-	-
Пропорционального деления	-	+	-
Интегральный	+	-	+
Логарифмический	+	-	-

Следует иметь в виду, что при факторном анализе аддитивных моделей, используется метод прямого счёта. Например, изменение ресурсов банка за счёт каждого фактора тождественно изменению самого фактора. Математически это можно представить следующим образом.

∆ РБ_деп= ∆ ДБ – изменение депозитов банка

∆ РБ_КР=∆ КБ – изменение полученных кредитов

∆ РБ_ПР=∆ ПС – изменение привлечённых средств

∆ РБ_СС=∆ СС – изменение собственных средств