В этом параграфе мы используем обозначения, введенные в § 3.1, частности, мы считаем, что эллипс, гипербола и парабола заданы в прямоугольной системе координат каноническими уравнениями соответственно (1), (3) и (6) из § 3.1.
Определение 3.3.1. Директрисами эллипса и гиперболы называются две прямые  и
и  с уравнениями соответственно
с уравнениями соответственно  и
и  . Директрисой параболы называется прямая
. Директрисой параболы называется прямая  с уравнением
с уравнением 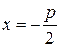 (рис. 7).
(рис. 7).
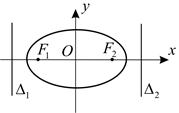


Рис. 7
Будем говорить, что в случаях эллипса и гиперболы фокус  и директриса
и директриса  соответствуют друг другу. Первое общее свойство трех упомянутых фигур выражается следующим утверждением.
соответствуют друг другу. Первое общее свойство трех упомянутых фигур выражается следующим утверждением.
Утверждение 3.3.1. Для любой точки эллипса, гиперболы или параболы отношение ее расстояний до фокуса и соответствующей директрисы постоянно и равно эксцентриситету.
Доказательство. Пусть  – произвольная точкаэллипса,
– произвольная точкаэллипса,  – расстояние от
– расстояние от  до левого фокуса
до левого фокуса  (см. § 3.1),
(см. § 3.1),  – расстояние от
– расстояние от  до левой директрисы
до левой директрисы  . Тогда
. Тогда  . Для правых фокуса и директрисы доказательство аналогично.
. Для правых фокуса и директрисы доказательство аналогично.
Пусть  – произвольная точкагиперболы,
– произвольная точкагиперболы,  – расстояние от
– расстояние от  до правого фокуса
до правого фокуса  (см. § 3.1),
(см. § 3.1), 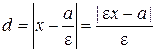 – расстояние от
– расстояние от  до правой директрисы
до правой директрисы  . Тогда
. Тогда  . Для левых фокуса и директрисы доказательство аналогично.
. Для левых фокуса и директрисы доказательство аналогично.
Пусть  – произвольная точкапараболы, тогда
– произвольная точкапараболы, тогда 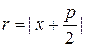 – расстояние от
– расстояние от  до фокуса
до фокуса  (см. § 3.1),
(см. § 3.1),  – расстояние от
– расстояние от  до директрисы
до директрисы  . Тогда
. Тогда 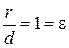 .
.
Доказанное свойство является характеристическим для трех фигур.
Утверждение 3.3.2. Пусть  – прямая на плоскости
– прямая на плоскости  ,
,  – точка плоскости, не лежащая на
– точка плоскости, не лежащая на  ,
,  – положительное число.
– положительное число.
Тогда фигура  , состоящая из всех точек плоскости, для которых отношение расстояний до точки
, состоящая из всех точек плоскости, для которых отношение расстояний до точки  и до прямой
и до прямой  постоянно и равно
постоянно и равно  , суть: эллипс, если
, суть: эллипс, если 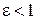 ; гипербола, если
; гипербола, если 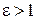 ; парабола, если
; парабола, если  .
.
Коротко заключение утверждения можно записать следующим образом:
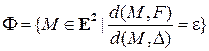 –
– 
Доказательство. Выберем прямоугольную систему координат  на плоскости
на плоскости  так, что ось
так, что ось 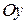 совпадает с прямой
совпадает с прямой  , а ось
, а ось 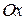 проходит через точку
проходит через точку  перпендикулярно
перпендикулярно  . Тогда координаты заданной точки:
. Тогда координаты заданной точки:  , где
, где  – расстояние от
– расстояние от  до
до  . Если
. Если  – произвольная точка плоскости, то уравнение фигуры
– произвольная точка плоскости, то уравнение фигуры  имеет вид:
имеет вид:
 или
или 
Преобразовывая уравнение далее, получим:
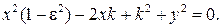 (1)
(1)
Пусть  . Вынесем множитель
. Вынесем множитель  из слагаемых, содержащих
из слагаемых, содержащих  , и дополним оставшиеся члены до полного квадрата:
, и дополним оставшиеся члены до полного квадрата:
 или
или
 .
.
Введем обозначение 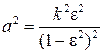 и разделим обе части последнего уравнения на
и разделим обе части последнего уравнения на  . Получим в итоге следующее уравнение фигуры
. Получим в итоге следующее уравнение фигуры  :
:
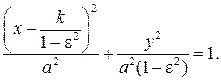 (2)
(2)
Очевидно, что (2) является уравнением эллипса, если 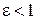 , и уравнением гиперболы, если
, и уравнением гиперболы, если 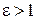 .
.
Если  в уравнении (1), то его можно переписать в виде
в уравнении (1), то его можно переписать в виде  . Последнее уравнение, очевидно, задает параболу.
. Последнее уравнение, очевидно, задает параболу.
Читателю предлагается в качестве упражнения убедиться в том, что  и
и  являются для фигуры
являются для фигуры  соответствующими друг другу фокусом и директрисой.
соответствующими друг другу фокусом и директрисой.
Второе общее свойство эллипса, гиперболы и параболы, которое мы отметим, заключается в том, что при подходящем выборе полярной системы координат все три фигуры можно задать одним уравнением.
Пусть  – эллипс, гипербола или парабола,
– эллипс, гипербола или парабола,  и
и  соответствующие друг другу фокус и директриса. Зададим полярную систему координат следующим образом. Полюс поместим в точку
соответствующие друг другу фокус и директриса. Зададим полярную систему координат следующим образом. Полюс поместим в точку  , полярный луч выберем перпендикулярным прямой
, полярный луч выберем перпендикулярным прямой  , но не пересекающим ее (рис. 8).
, но не пересекающим ее (рис. 8).
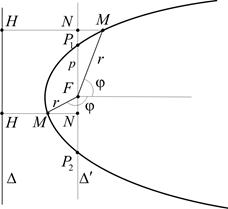
Рис. 8
Прямая 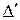 , проходящая через точку
, проходящая через точку  перпендикулярно полярному лучу, пересекает фигуру
перпендикулярно полярному лучу, пересекает фигуру  в двух симметричных относительно
в двух симметричных относительно  точках
точках  и
и  . Пусть
. Пусть  – одна из них. Число
– одна из них. Число  называется фокальным параметром фигуры
называется фокальным параметром фигуры  . В силу утверждения 3.3.1, для каждой из трех фигур
. В силу утверждения 3.3.1, для каждой из трех фигур  где
где  – эксцентриситет фигуры
– эксцентриситет фигуры  ,
,  – расстояние от
– расстояние от  до
до  (или, что то же самое, расстояние между параллельными прямыми
(или, что то же самое, расстояние между параллельными прямыми  и
и 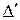 ). Несложные вычисления показывают, что для параболы
). Несложные вычисления показывают, что для параболы  совпадает с числом
совпадает с числом  в ее каноническом уравнении, а для эллипса и гиперболы
в ее каноническом уравнении, а для эллипса и гиперболы  где
где  и
и  – полуоси. Пусть
– полуоси. Пусть  – произвольная точка эллипса, параболы или той ветви гиперболы, которая лежит между
– произвольная точка эллипса, параболы или той ветви гиперболы, которая лежит между  и
и  , заданная своими полярными координатами,
, заданная своими полярными координатами,  – точка пересечения прямой
– точка пересечения прямой 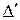 и перпендикуляра
и перпендикуляра  к прямой
к прямой  , проведенного из точки
, проведенного из точки  . Если точка
. Если точка  не совпадает с
не совпадает с  или
или  , то
, то 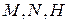 три попарно различные точки одной прямой и возможны два варианта их взаимного расположения: либо
три попарно различные точки одной прямой и возможны два варианта их взаимного расположения: либо  лежит между
лежит между  и
и  (рис. 8, верхняя часть), либо
(рис. 8, верхняя часть), либо  лежит между
лежит между  и
и  (рис. 8, нижняя часть). Расстояние от точки
(рис. 8, нижняя часть). Расстояние от точки  до директрисы
до директрисы  равно
равно  в первом случае и
в первом случае и 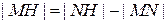 во втором случае. В обоих случаях
во втором случае. В обоих случаях  =
= 
 в первом случае и
в первом случае и 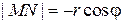 во втором случае. В итоге, в обоих случаях имеем:
во втором случае. В итоге, в обоих случаях имеем:  В силу утверждения 3.3.1,
В силу утверждения 3.3.1,  , или
, или  Выражая из последнего равенства
Выражая из последнего равенства  через
через  , получаем окончательно полярное уравнение
, получаем окончательно полярное уравнение
 , (3)
, (3)
которое задает эллипс, параболу или одну ветвь гиперболы.
Далее мы найдем уравнения касательных прямых к эллипсу, гиперболе, параболе.
Если ограничиться первой координатной четвертью, то дуга эллипса, лежащая в этой четверти, является графиком функции

Из школьного курса математики известно, что уравнение касательной к графику функции  в точке
в точке  имеет вид:
имеет вид:
 .
.
В рассматриваемом случае
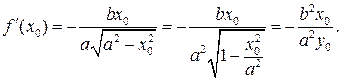
Следовательно, уравнение касательной:
 или
или  .
.
Так как  , получаем окончательно уравнение касательной к эллипсу в точке
, получаем окончательно уравнение касательной к эллипсу в точке  :
:
 . (4)
. (4)
Учитывая, что эллипс симметричен относительно координатных осей, нетрудно убедиться, что по формуле (4) задается касательная к эллипсу в его произвольной точке.
Аналогично получаются уравнения касательных к гиперболе:
 (5)
(5)
и параболе:
 (6)
(6)
Теперь можно установить так называемые «оптические» свойства эллипса, гиперболы и параболы.
Утверждение 3.3.3. Касательная в любой точке эллипса или гиперболы составляют равные углы с фокальными радиусами этой точки (рис. 9).

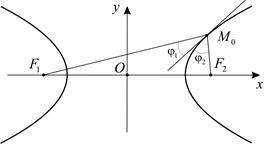
Рис. 9
Доказательство. Пусть  – точка эллипса. Рассмотрим векторы
– точка эллипса. Рассмотрим векторы  и
и  , а также направляющий вектор
, а также направляющий вектор  касательной. Пусть
касательной. Пусть  и
и  – величины углов соответственно между
– величины углов соответственно между  и
и  , и между
, и между 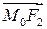 и
и  .Тогда:
.Тогда:

 Таким образом,
Таким образом, 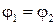 . Доказательство в случае гиперболы проводится аналогично.
. Доказательство в случае гиперболы проводится аналогично.
Физическая (оптическая) интерпретация доказанных свойств следующая:
луч, выпущенный из одного фокуса эллипса, отразившись от эллипса, попадает в другой фокус;
луч, выпущенный из одного фокуса, отразившись от гиперболы, идет по прямой, проходящей через второй фокус и точку отражения.
Утверждение 3.3.4. Касательная в любой точке параболы составляют равные углы с фокальным радиусом этой точки и осью параболы (рис. 10).

Рис. 10
Доказательство. Пусть  – точка параболы. Рассмотрим вектор
– точка параболы. Рассмотрим вектор  и направляющий вектор
и направляющий вектор  касательной. Пусть
касательной. Пусть  и
и  – величины углов соответственно между
– величины углов соответственно между  и
и  , и между
, и между  и осью параболы. Поскольку в рассматриваемом случае ось параболы совпадает с координатной осью
и осью параболы. Поскольку в рассматриваемом случае ось параболы совпадает с координатной осью 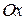 , то
, то  – величина угла между
– величина угла между  и базисным вектором
и базисным вектором  системы координат. Тогда:
системы координат. Тогда:

 Таким образом,
Таким образом, 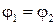 .
.
Физическая (оптическая) интерпретация доказанного свойства параболы следующая: луч, выпущенный из фокуса, отразившись от параболы, идет по прямой, параллельной оси параболы. На этом свойстве основаны конструкции прожекторов, фар, передающих и принимающих антенн, в том числе параболических телевизионных.

 и
и  с уравнениями соответственно
с уравнениями соответственно  и
и  . Директрисой параболы называется прямая
. Директрисой параболы называется прямая  с уравнением
с уравнением 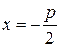 (рис. 7).
(рис. 7).


 и директриса
и директриса  соответствуют друг другу. Первое общее свойство трех упомянутых фигур выражается следующим утверждением.
соответствуют друг другу. Первое общее свойство трех упомянутых фигур выражается следующим утверждением. – произвольная точкаэллипса,
– произвольная точкаэллипса,  – расстояние от
– расстояние от  до левого фокуса
до левого фокуса  (см. § 3.1),
(см. § 3.1),  – расстояние от
– расстояние от  . Для правых фокуса и директрисы доказательство аналогично.
. Для правых фокуса и директрисы доказательство аналогично. – расстояние от
– расстояние от 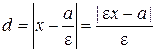 – расстояние от
– расстояние от 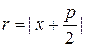 – расстояние от
– расстояние от  (см. § 3.1),
(см. § 3.1),  – расстояние от
– расстояние от  . Тогда
. Тогда 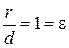 .
. ,
,  – положительное число.
– положительное число. , состоящая из всех точек плоскости, для которых отношение расстояний до точки
, состоящая из всех точек плоскости, для которых отношение расстояний до точки 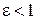 ; гипербола, если
; гипербола, если 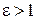 ; парабола, если
; парабола, если  .
.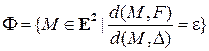 –
– 
 на плоскости
на плоскости 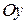 совпадает с прямой
совпадает с прямой 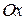 проходит через точку
проходит через точку  , где
, где  – расстояние от
– расстояние от  или
или 
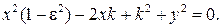 (1)
(1) . Вынесем множитель
. Вынесем множитель  из слагаемых, содержащих
из слагаемых, содержащих  , и дополним оставшиеся члены до полного квадрата:
, и дополним оставшиеся члены до полного квадрата: или
или .
.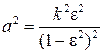 и разделим обе части последнего уравнения на
и разделим обе части последнего уравнения на  . Получим в итоге следующее уравнение фигуры
. Получим в итоге следующее уравнение фигуры 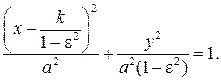 (2)
(2) . Последнее уравнение, очевидно, задает параболу.
. Последнее уравнение, очевидно, задает параболу. 
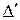 , проходящая через точку
, проходящая через точку  и
и  . Пусть
. Пусть  – одна из них. Число
– одна из них. Число  называется фокальным параметром фигуры
называется фокальным параметром фигуры  где
где  – эксцентриситет фигуры
– эксцентриситет фигуры  – расстояние от
– расстояние от  совпадает с числом
совпадает с числом  где
где  и
и  – полуоси. Пусть
– полуоси. Пусть  – произвольная точка эллипса, параболы или той ветви гиперболы, которая лежит между
– произвольная точка эллипса, параболы или той ветви гиперболы, которая лежит между  – точка пересечения прямой
– точка пересечения прямой  к прямой
к прямой 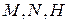 три попарно различные точки одной прямой и возможны два варианта их взаимного расположения: либо
три попарно различные точки одной прямой и возможны два варианта их взаимного расположения: либо  (рис. 8, верхняя часть), либо
(рис. 8, верхняя часть), либо  в первом случае и
в первом случае и 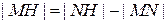 во втором случае. В обоих случаях
во втором случае. В обоих случаях  =
= 
 в первом случае и
в первом случае и 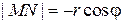 во втором случае. В итоге, в обоих случаях имеем:
во втором случае. В итоге, в обоих случаях имеем:  В силу утверждения 3.3.1,
В силу утверждения 3.3.1,  , или
, или  Выражая из последнего равенства
Выражая из последнего равенства  через
через  , получаем окончательно полярное уравнение
, получаем окончательно полярное уравнение , (3)
, (3)
 в точке
в точке  имеет вид:
имеет вид: .
.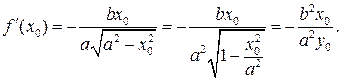
 или
или  .
. , получаем окончательно уравнение касательной к эллипсу в точке
, получаем окончательно уравнение касательной к эллипсу в точке  . (4)
. (4) (5)
(5) (6)
(6)

 и
и  , а также направляющий вектор
, а также направляющий вектор  касательной. Пусть
касательной. Пусть  и
и  – величины углов соответственно между
– величины углов соответственно между  и
и  , и между
, и между 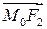 и
и 
 Таким образом,
Таким образом, 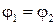 . Доказательство в случае гиперболы проводится аналогично.
. Доказательство в случае гиперболы проводится аналогично. 
 и направляющий вектор
и направляющий вектор  касательной. Пусть
касательной. Пусть  и
и  системы координат. Тогда:
системы координат. Тогда:
 Таким образом,
Таким образом, 


