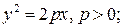ФИГУРЫ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ
Определение 3.2.1. Фигурой второго порядка на плоскости  называется фигура, которая в некотором аффинном репере может быть задана уравнением второй степени от двух неизвестных.
называется фигура, которая в некотором аффинном репере может быть задана уравнением второй степени от двух неизвестных.
Таким образом, фигура 
 является фигурой второго порядка, если существует аффинный репер
является фигурой второго порядка, если существует аффинный репер  в котором
в котором  задается уравнением:
задается уравнением:
 (1)
(1)
В уравнении (1)  – фиксированные вещественные числа,
– фиксированные вещественные числа,  – неизвестные, коэффициент 2 в трех слагаемых поставлен для удобства дальнейших преобразований уравнения. Поскольку (1) – уравнение второй степени, среди коэффициентов
– неизвестные, коэффициент 2 в трех слагаемых поставлен для удобства дальнейших преобразований уравнения. Поскольку (1) – уравнение второй степени, среди коэффициентов  есть ненулевые. Это условие можно записать в матричном виде:
есть ненулевые. Это условие можно записать в матричном виде:
 (2)
(2)
Утверждение 3.2.1. Фигура  , которая в репере
, которая в репере  задана уравнением (1) с условием (2), в любом другом репере
задана уравнением (1) с условием (2), в любом другом репере 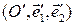 может быть задана уравнением такого же типа.
может быть задана уравнением такого же типа.
Доказательство. Будем использовать матричные обозначения. У нас уже есть матрица  коэффициентов квадратичной части уравнения. Обозначим
коэффициентов квадратичной части уравнения. Обозначим  строку коэффициентов линейной части и
строку коэффициентов линейной части и  – столбец неизвестных. В таких обозначениях уравнение (1) переписывается в виде:
– столбец неизвестных. В таких обозначениях уравнение (1) переписывается в виде:
 (
(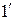 )
)
Чтобы найти уравнение фигуры  в репере
в репере  запишем формулы преобразования координат точек (формулы (2) из § 2.1) при переходе от репера
запишем формулы преобразования координат точек (формулы (2) из § 2.1) при переходе от репера  к реперу
к реперу 
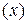 =
=  (2)
(2)
и подставим выражение 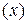 из (2) в уравнение (
из (2) в уравнение (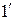 ). Получим:
). Получим:


Таким образом, уравнение  в репере
в репере 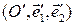 имеет такой же вид, как уравнение (
имеет такой же вид, как уравнение (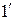 ):
):
 (
( )
)
где 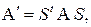
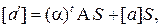
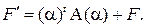 Покажем, что
Покажем, что  – ненулевая матрица. Рассуждаем «методом от противного». Допустим, что
– ненулевая матрица. Рассуждаем «методом от противного». Допустим, что  Запишем формулы преобразования координат при обратном переходе от репера
Запишем формулы преобразования координат при обратном переходе от репера 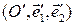 к реперу
к реперу 
 Если подставить это выражение
Если подставить это выражение  в уравнение (3), то получим исходное уравнение (
в уравнение (3), то получим исходное уравнение (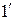 ). При этом, как и при первом переходе, матрица
). При этом, как и при первом переходе, матрица  коэффициентов квадратичной части равна:
коэффициентов квадратичной части равна:  По сделанному нами допущению,
По сделанному нами допущению,  следовательно,
следовательно,  Получили противоречие с условием
Получили противоречие с условием  что и завершает доказательство.
что и завершает доказательство.
Далее мы выясним, какие бывают фигуры второго порядка. Зафиксируем на плоскости ортонормированный репер  Согласно утверждению 3.1.1, любая фигура второго порядка
Согласно утверждению 3.1.1, любая фигура второго порядка  в этом репере имеет уравнение (1). Предположим, что в этом уравнении коэффициент при произведении неизвестных отличен от нуля:
в этом репере имеет уравнение (1). Предположим, что в этом уравнении коэффициент при произведении неизвестных отличен от нуля:  Покажем, что повернув репер
Покажем, что повернув репер  вокруг начала координат на подходящий угол
вокруг начала координат на подходящий угол  , т.е. перейдя к другому ортонормированному реперу
, т.е. перейдя к другому ортонормированному реперу  можно добиться того, что в новом репере фигура
можно добиться того, что в новом репере фигура  имеет уравнение вида (1) с нулевым коэффициентом при произведении неизвестных. Запишем формулы преобразования координат при повороте прямоугольной системы координат вокруг точки
имеет уравнение вида (1) с нулевым коэффициентом при произведении неизвестных. Запишем формулы преобразования координат при повороте прямоугольной системы координат вокруг точки  на угол
на угол  (см. § 2.1):
(см. § 2.1):
 (4)
(4)
Подставив выражения  и
и  в уравнение (1), получим уравнение вида (1) фигуры
в уравнение (1), получим уравнение вида (1) фигуры  в системе координат
в системе координат  Нас интересует коэффициент
Нас интересует коэффициент  при произведении неизвестных
при произведении неизвестных 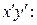
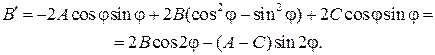
Если угол  выбрать таким, что
выбрать таким, что

то  Таким образом, можно считать, что в подходящей прямоугольной системе координат
Таким образом, можно считать, что в подходящей прямоугольной системе координат  фигура
фигура  имеет уравнение
имеет уравнение
 (5)
(5)
причем коэффициенты  и
и  не равны нулю одновременно. Рассмотрим несколько вариантов.
не равны нулю одновременно. Рассмотрим несколько вариантов.
I. Пусть  Преобразуем левую часть уравнения (5) следующим образом:
Преобразуем левую часть уравнения (5) следующим образом:

Произведем параллельный перенос системы координат

согласно формулам:

В новой системе координат уравнение фигуры  имеет вид:
имеет вид:
 (6)
(6)
 . Пусть
. Пусть  В этом случае, положив
В этом случае, положив  уравнение (6) можно записать в виде:
уравнение (6) можно записать в виде:
 (7)
(7)
Таким образом, в случае  фигура
фигура  является эллипсом.
является эллипсом.
 . Пусть
. Пусть  В этом случае, положив
В этом случае, положив  уравнение (6) можно записать в виде:
уравнение (6) можно записать в виде:
 (8)
(8)
Таким образом, в случае  фигура
фигура  является гиперболой.
является гиперболой.
 . Пусть
. Пусть  В этом случае, положив
В этом случае, положив  уравнение (6) можно записать в виде:
уравнение (6) можно записать в виде:
 или
или  (9)
(9)
Таким образом, в случае  фигура
фигура  является парой прямых, пересекающихся в начале координат с уравнениями:
является парой прямых, пересекающихся в начале координат с уравнениями:  и
и 
 . Пусть
. Пусть  В этом случае, положив
В этом случае, положив  уравнение (6) можно записать в виде:
уравнение (6) можно записать в виде:
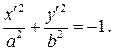 (10)
(10)
Уравнение (10) не имеет решений в области действительных чисел, поэтому на плоскости  фигура
фигура  сводится к пустому множеству. Тем не менее, фигуру с уравнением (10) принято называть мнимым эллипсом, учитывая, что в области комплексных чисел уравнение (10) имеет решения.
сводится к пустому множеству. Тем не менее, фигуру с уравнением (10) принято называть мнимым эллипсом, учитывая, что в области комплексных чисел уравнение (10) имеет решения.
 . Пусть
. Пусть  В этом случае, положив
В этом случае, положив  уравнение (6) можно записать в виде:
уравнение (6) можно записать в виде:
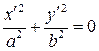 (11)
(11)
Уравнение (11) в области действительных чисел имеет единственное решение  , поэтому на плоскости
, поэтому на плоскости  фигура
фигура  сводится к точке. В области комплексных чисел левая часть уравнения (11) распадается на линейные множители:
сводится к точке. В области комплексных чисел левая часть уравнения (11) распадается на линейные множители:
 ,
,
поэтому фигуру  с уравнением (11) по аналогии со случаем
с уравнением (11) по аналогии со случаем  принято называть парой мнимых прямых, пересекающихся в действительной точке
принято называть парой мнимых прямых, пересекающихся в действительной точке 
Читателю предлагается в качестве упражнения убедиться, что в случае I иных фигур, кроме пяти перечисленных выше, не возникает.
 . Пусть
. Пусть  Преобразуем левую часть уравнения (5) следующим образом:
Преобразуем левую часть уравнения (5) следующим образом:

Произведем параллельный перенос системы координат

согласно формулам:

В новой системе координат уравнение фигуры  имеет вид:
имеет вид:
 (12)
(12)
Этом случае возможны следующие 3 варианта.
 . Пусть
. Пусть  В этом случае, положив
В этом случае, положив  уравнение (12) можно записать в виде:
уравнение (12) можно записать в виде:
 или
или 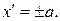 (13)
(13)
Таким образом, в случае  фигура
фигура  является парой параллельных прямых.
является парой параллельных прямых.
 . Пусть
. Пусть  В этом случае, положив
В этом случае, положив  уравнение (12) можно записать в виде:
уравнение (12) можно записать в виде:
 (13)
(13)
В этом случае фигуру  принято называть парой мнимых параллельных прямых.
принято называть парой мнимых параллельных прямых.
 . Пусть
. Пусть  В этом случае уравнение (12) можно записать в виде:
В этом случае уравнение (12) можно записать в виде:
 (14)
(14)
Уравнение (14) задает прямую. Учитывая вторую степень уравнения, фигуру  в этом случае принято называть сдвоенной прямой.
в этом случае принято называть сдвоенной прямой.
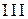 . Пусть
. Пусть  Преобразуем левую часть уравнения (5) следующим образом:
Преобразуем левую часть уравнения (5) следующим образом:

Произведем параллельный перенос системы координат

согласно формулам:

В новой системе координат уравнение фигуры  имеет вид:
имеет вид:
 (15)
(15)
где  Фигура
Фигура  является параболой.
является параболой.
Зафиксируем итог наших рассмотрений в следующей теореме.
Теорема 3.1.1. Для любой фигуры  второго порядка на плоскости
второго порядка на плоскости  существует прямоугольная система координат
существует прямоугольная система координат  , в которой
, в которой  задается одним из следующих канонических уравнений:
задается одним из следующих канонических уравнений:
1) 
 – эллипс;
– эллипс;
2) 
 – гипербола;
– гипербола;
3) 
 – пара пересекающихся прямых;
– пара пересекающихся прямых;
4) 
 – мнимый эллипс;
– мнимый эллипс;
5) 
 – пара мнимых прямых, пересекающихся в действительной точке;
– пара мнимых прямых, пересекающихся в действительной точке;
6) 
 – пара параллельных прямых;
– пара параллельных прямых;
7) 
 – пара мнимых параллельных прямых;
– пара мнимых параллельных прямых;
8) 
 – сдвоенная прямая;
– сдвоенная прямая;
9) 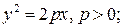
 – парабола.
– парабола.

 называется фигура, которая в некотором аффинном репере может быть задана уравнением второй степени от двух неизвестных.
называется фигура, которая в некотором аффинном репере может быть задана уравнением второй степени от двух неизвестных.
 является фигурой второго порядка, если существует аффинный репер
является фигурой второго порядка, если существует аффинный репер  в котором
в котором  задается уравнением:
задается уравнением: (1)
(1) – фиксированные вещественные числа,
– фиксированные вещественные числа,  – неизвестные, коэффициент 2 в трех слагаемых поставлен для удобства дальнейших преобразований уравнения. Поскольку (1) – уравнение второй степени, среди коэффициентов
– неизвестные, коэффициент 2 в трех слагаемых поставлен для удобства дальнейших преобразований уравнения. Поскольку (1) – уравнение второй степени, среди коэффициентов  есть ненулевые. Это условие можно записать в матричном виде:
есть ненулевые. Это условие можно записать в матричном виде: (2)
(2) задана уравнением (1) с условием (2), в любом другом репере
задана уравнением (1) с условием (2), в любом другом репере 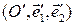 может быть задана уравнением такого же типа.
может быть задана уравнением такого же типа. коэффициентов квадратичной части уравнения. Обозначим
коэффициентов квадратичной части уравнения. Обозначим  строку коэффициентов линейной части и
строку коэффициентов линейной части и  – столбец неизвестных. В таких обозначениях уравнение (1) переписывается в виде:
– столбец неизвестных. В таких обозначениях уравнение (1) переписывается в виде: (
(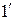 )
) запишем формулы преобразования координат точек (формулы (2) из § 2.1) при переходе от репера
запишем формулы преобразования координат точек (формулы (2) из § 2.1) при переходе от репера 
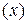 =
=  (2)
(2)

 (
( )
)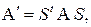
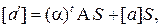
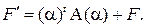 Покажем, что
Покажем, что  – ненулевая матрица. Рассуждаем «методом от противного». Допустим, что
– ненулевая матрица. Рассуждаем «методом от противного». Допустим, что  Запишем формулы преобразования координат при обратном переходе от репера
Запишем формулы преобразования координат при обратном переходе от репера 
 Если подставить это выражение
Если подставить это выражение  в уравнение (3), то получим исходное уравнение (
в уравнение (3), то получим исходное уравнение ( По сделанному нами допущению,
По сделанному нами допущению,  следовательно,
следовательно,  Получили противоречие с условием
Получили противоречие с условием  что и завершает доказательство.
что и завершает доказательство.  Согласно утверждению 3.1.1, любая фигура второго порядка
Согласно утверждению 3.1.1, любая фигура второго порядка  Покажем, что повернув репер
Покажем, что повернув репер  вокруг начала координат на подходящий угол
вокруг начала координат на подходящий угол  , т.е. перейдя к другому ортонормированному реперу
, т.е. перейдя к другому ортонормированному реперу  можно добиться того, что в новом репере фигура
можно добиться того, что в новом репере фигура  на угол
на угол  (4)
(4) и
и  в уравнение (1), получим уравнение вида (1) фигуры
в уравнение (1), получим уравнение вида (1) фигуры  Нас интересует коэффициент
Нас интересует коэффициент  при произведении неизвестных
при произведении неизвестных 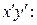
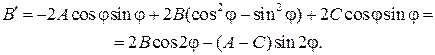

 Таким образом, можно считать, что в подходящей прямоугольной системе координат
Таким образом, можно считать, что в подходящей прямоугольной системе координат  (5)
(5) и
и  не равны нулю одновременно. Рассмотрим несколько вариантов.
не равны нулю одновременно. Рассмотрим несколько вариантов. Преобразуем левую часть уравнения (5) следующим образом:
Преобразуем левую часть уравнения (5) следующим образом:


 (6)
(6) . Пусть
. Пусть  В этом случае, положив
В этом случае, положив  уравнение (6) можно записать в виде:
уравнение (6) можно записать в виде: (7)
(7) . Пусть
. Пусть  В этом случае, положив
В этом случае, положив  уравнение (6) можно записать в виде:
уравнение (6) можно записать в виде: (8)
(8) . Пусть
. Пусть  В этом случае, положив
В этом случае, положив  уравнение (6) можно записать в виде:
уравнение (6) можно записать в виде: или
или  (9)
(9) и
и 
 . Пусть
. Пусть  В этом случае, положив
В этом случае, положив  уравнение (6) можно записать в виде:
уравнение (6) можно записать в виде: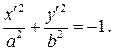 (10)
(10) . Пусть
. Пусть  В этом случае, положив
В этом случае, положив  уравнение (6) можно записать в виде:
уравнение (6) можно записать в виде: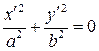 (11)
(11) , поэтому на плоскости
, поэтому на плоскости  ,
,
 . Пусть
. Пусть  Преобразуем левую часть уравнения (5) следующим образом:
Преобразуем левую часть уравнения (5) следующим образом:

 (12)
(12) . Пусть
. Пусть  В этом случае, положив
В этом случае, положив  уравнение (12) можно записать в виде:
уравнение (12) можно записать в виде: или
или 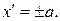 (13)
(13) . Пусть
. Пусть  В этом случае, положив
В этом случае, положив  уравнение (12) можно записать в виде:
уравнение (12) можно записать в виде: (13)
(13) . Пусть
. Пусть  В этом случае уравнение (12) можно записать в виде:
В этом случае уравнение (12) можно записать в виде: (14)
(14)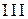 . Пусть
. Пусть  Преобразуем левую часть уравнения (5) следующим образом:
Преобразуем левую часть уравнения (5) следующим образом:

 (15)
(15) Фигура
Фигура  , в которой
, в которой