Способы задания движения точки
Для решения задач кинематики необходимо, чтобы изучаемое движение было задано. Оно считается заданным, если в любой момент времени однозначно можно определить положение точки в пространстве относительно заданной системы отсчета. Используют три основных способа задания движения точки: векторный, координатный и естественный. Векторный способ. Положение движущейся точки М в любой момент времени можно определить с помощью ее радиус-вектора, проведенного из центра О, связанного с телом отсчета, в точку М (рис. 1.1). Чтобы задать движение векторным способом, необходимо определить векторную функцию времени в виде:
Зависимость (1.1) называют уравнением движения точки в векторной форме. Начало радиус-вектора движущейся точки находится в точке О, а конец его перемещается по траектории вместе с точкой М. Геометрическое место концов радиус-вектора, т.е. годограф этого вектора, определяет траекторию движущейся точки. Координатный способ. С телом отсчета связывают прямоугольную систему декартовых координат, при этом положение точки определяют ее координатами, которые являются скалярными функциями времени (рис. 1.2):
Уравнения (1.2) называют уравнениями движения точки в координатной форме. Они являются параметрическими уравнениями траектории точки. Исключив из этих уравнений параметр – время, можно получить уравнение траектории.
Между способами задания движения точки имеется связь. Так, если начало декартовой системы координат совпадает с центром, из которого проводится радиус-вектор точки при векторном способе изучения ее движения (см. рис. 1.2), то координаты точки равны проекциям на соответствующие оси радиус-вектора точки
где Естественный способ. Этот способ используют в тех случаях, когда заранее известна траектория точки. На траектории выбирают неподвижную точку О (начало отсчета), а также положительное и отрицательное направления отсчета расстояний точки от начала отсчета (рис. 1.3). Тогда положение точки М на траектории будет однозначно определяться зависимостью криволинейной координаты S = ОМ от времени
где
|

 (1.1)
(1.1)
 (1.2)
(1.2)
 ,
,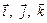 – единичные орты координатных осей.
– единичные орты координатных осей. (1.3)
(1.3) Связь между координатным и естественным способами определяется выражением
Связь между координатным и естественным способами определяется выражением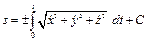 ,
, – первые производные от координат точки по времени; С – постоянная интегрирования, зависящая от начальных условий.
– первые производные от координат точки по времени; С – постоянная интегрирования, зависящая от начальных условий.


