Вращение твердого тела вокруг неподвижной оси
Вращением вокруг неподвижной оси называют такое движение твердого тела, при котором две какие-либо точки, принадлежащие телу, остаются неподвижными. Прямую, проходящую через эти точки, называют осью вращения тела. Перемещение тела из одного положения в другое называют поворотом. Все точки тела, лежащие на оси вращения, неподвижны. Все точки, не лежащие на оси вращения, описывают окружности, плоскости которых перпендикулярны оси вращения, а центры расположены на оси. Тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы, так как его положение в пространстве в любой момент времени полностью определяется одним независимым параметром – плоским углом j между двумя плоскостями: неподвижной и подвижной, жестко связанной с вращающимся телом (рис. 2.1). Этот угол называют угломповорота тела и измеряют в радианах. При этом принято считать угол поворота j положительным, если поворот тела, наблюдаемый с положительного направления оси Оz, виден происходящим против хода часовой стрелки. Таким образом, закон вращательного движения можно считать установленным, если задан угол поворота тела как функция времени
Основными кинематическими характеристиками вращательного движения тела в целом являются угловая скорость и угловое ускорение. Угловая скорость тела – это векторная величина, характеризующая интенсивность и направление изменения угла поворота тела.
Алгебраическое значение угловой скорости равно первой производной по времени от угла поворота тела
Угловое ускорение тела – это векторная величина, характеризующая интенсивность изменения угловой скорости. Алгебраическое значение углового ускорения равно первой производной по времени от угловой скорости тела или второй производной по времени от угла поворота тела
Размерность угловой скорости в системе СИ – рад/с, размерность углового ускорения – рад/с2. Число оборотов тела N и число оборотов в минуту n связаны с углом поворота j(t)и угловой скоростью j = 2p N рад;
Установим зависимости между общими кинематическими характеристиками вращательного движения тела в целом, а также скоростями и ускорениями различных точек этого тела. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, лежащие в плоскостях, перпендикулярных оси вращения, радиусы которых равны расстояниям от этих точек до оси вращения. Применяя естественный способ задания движения точки тела и учитывая, что
где v – алгебраическое значение скорости точки М;
Из приведенных формул видно, что скорости, ускорения и составляющие ускорения точек тела, вращающегося вокруг неподвижной оси, пропорциональны расстояниям от точек до оси вращения тела. Приведем также векторные формулы, описывающие кинематические характеристики тела и его точек (см. рис. 2.1), для чего введем векторы угловой скорости и углового ускорения
где Скорость и ускорение точки тела определим по формулам:
где Вращение называют равномерным, если в процессе движения угловая скорость остается постоянной по модулю и по направлению, т.е., если
Вращение называют равнопеременным, если угловое ускорение тела в процессе движения остается постоянным по модулю и направлению, т.е., если
Так как
|

 . (2.6)
. (2.6)
 . (2.7)
. (2.7)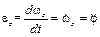 . (2.8)
. (2.8) следующими зависимостями:
следующими зависимостями: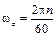 рад/с.
рад/с. , где h – расстояние от точки до оси вращения тела (см. рис. 2.1), для скорости и ускорения точки М запишем
, где h – расстояние от точки до оси вращения тела (см. рис. 2.1), для скорости и ускорения точки М запишем (2.9)
(2.9) (2.10)
(2.10) (2.11)
(2.11)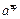 и
и  – алгебраические значения составляющих полного вектора ускорения этой точки. Здесь величины
– алгебраические значения составляющих полного вектора ускорения этой точки. Здесь величины  . (2.12)
. (2.12) (2.13)
(2.13) – единичный вектор оси, совпадающий по направлению с положительным направлением оси вращения тела;
– единичный вектор оси, совпадающий по направлению с положительным направлением оси вращения тела;  и
и  – величины, имеющие смысл проекций векторов угловой скорости и углового ускорения на ось вращения тела. Таким образом, вектор угловой скорости располагается на оси вращения и направлен так, что с его вершины вращение тела наблюдается против стрелки часов. Вектор углового ускорения тоже располагается на оси вращения. Если знаки
– величины, имеющие смысл проекций векторов угловой скорости и углового ускорения на ось вращения тела. Таким образом, вектор угловой скорости располагается на оси вращения и направлен так, что с его вершины вращение тела наблюдается против стрелки часов. Вектор углового ускорения тоже располагается на оси вращения. Если знаки  и
и  совпадают, то он направлен так же, как и вектор угловой скорости (вращение ускоренное), а в противном случае – противоположно вектору угловой скорости (вращение замедленное).
совпадают, то он направлен так же, как и вектор угловой скорости (вращение ускоренное), а в противном случае – противоположно вектору угловой скорости (вращение замедленное).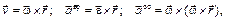 (2.14)
(2.14) – радиус-вектор точки, проведенный из любой точки на оси вращения тела, знак «
– радиус-вектор точки, проведенный из любой точки на оси вращения тела, знак « » означает векторное произведение.
» означает векторное произведение. . Умножив правую и левую части этого равенства на величину dt и проинтегрировав левую часть полученного равенства в пределах от
. Умножив правую и левую части этого равенства на величину dt и проинтегрировав левую часть полученного равенства в пределах от  до φ, а правую – от 0 до t, получим закон равномерного вращения:
до φ, а правую – от 0 до t, получим закон равномерного вращения: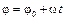 . (2.15)
. (2.15) . Чтобы найти закон изменения угловой скорости в этом случае, проинтегрируем левую часть равенства
. Чтобы найти закон изменения угловой скорости в этом случае, проинтегрируем левую часть равенства  пределах от
пределах от 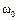 до
до  , а правую часть – от 0 до t:
, а правую часть – от 0 до t: . (2.16)
. (2.16)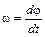 , то полученное выражение запишем в следующем виде
, то полученное выражение запишем в следующем виде  . Интегрируя это выражение при изменении угла поворота от
. Интегрируя это выражение при изменении угла поворота от  и времени от 0 до t, запишем закон равнопеременного вращения:
и времени от 0 до t, запишем закон равнопеременного вращения: . (2.17)
. (2.17)


