Определение скоростей и ускорений точек тела
Скорость любой точки В плоской фигуры равна геометрической сумме двух скоростей: скорости точки А, принятой в качестве полюса, и скорости точки В при вращении тела вокруг полюса (рис. 3.2, а)
где
Модуль и направление скорости
Еще один способ определения скоростей точек тела при плоскопараллельном движении основан на использовании теоремы о равенстве проекций скоростей двух точек тела: «Проекции скоростей двух точек тела на прямую, соединяющую эти точки, равны друг другу». Заметим, что эта теорема справедлива для любого вида движения абсолютно твердого тела и позволяет легко находить скорость точки тела, если известны направление скорости этой точки, а также направление и величина скорости какой-либо другой точки этого же тела. Ускорение любой точки В плоской фигуры равно геометрической сумме ускорения точки А, принятой в качестве полюса, и ускорения, которое точка приобретает при вращении тела вокруг полюса (рис. 3.2, б):
где
Определять полный вектор ускорения
|
, (3.4)
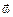– вектор угловой скорости, введенный так же, как и при рассмотрении вращения тела вокруг неподвижной оси (здесь этот вектор располагается на оси, проведенной через полюс перпендикулярно плоскости движения); 
– радиус-вектор точки М, проведенный из точки А. Вращательная составляющая скорости точки 
перпендикулярна отрезку AM и направлена в сторону вращения тела, ее модуль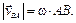
(3.5)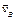
находят построением соответствующего параллелограмма (см. рис. 3.2, а).
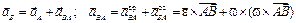, (3.6)
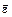– вектор углового ускорения, введенный так же, как и при рассмотрении вращения тела вокруг неподвижной оси. Вектор вращательной составляющей ускорения 
направлен перпендикулярно отрезку AB в сторону углового ускорения, т.е. в сторону вращения, если оно ускоренное, и в противоположную сторону, если замедленное. Вектор осестремительной составляющей ускорения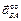 
всегда направлен от точки М к полюсу A. Запишем модули этих векторов соответственно
. (3.7)
точки М целесообразно не геометрически, а аналитически с помощью разложения слагаемых векторов на оси выбранной системы координат.
