Задание К3
4.3.1. Примеры решения контрольного задания К3
Пример 1. Катушка катится без скольжения в вертикальной плоскости по наклонному пути (рис. 4.5).
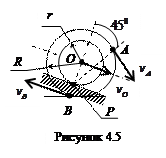 Найти угловую скорость катушки, скорости точек О и В, если в рассматриваемый момент времени Найти угловую скорость катушки, скорости точек О и В, если в рассматриваемый момент времени  = 2 м/с, = 2 м/с,
r = 0.6 м, R = 1 м.
Решение
Катушка совершает плоскопараллельное движение. Так как качение происходит без скольжения, то скорость точки Р касания катушки с неподвижной поверхностью 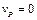 , следовательно эта точка является мгновенным центром скоростей (МЦС). Вектор скорости точки А , следовательно эта точка является мгновенным центром скоростей (МЦС). Вектор скорости точки А 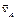 перпендикулярен АР и направлен в сторону качения катушки, а численное значение скорости пропорционально расстоянию от точки А до МЦС: перпендикулярен АР и направлен в сторону качения катушки, а численное значение скорости пропорционально расстоянию от точки А до МЦС:
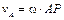 , ,
где 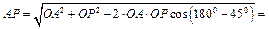
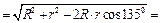 1, 49 м. 1, 49 м.
Определим угловую скорость катушки
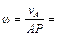 1, 35 рад/с. 1, 35 рад/с.
Так как скорости точек О и В катушки также пропорциональны их расстояниям до точки Р, то
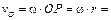 0, 81 м/с; 0, 81 м/с;
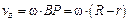 = 0, 54 м/с. = 0, 54 м/с.
Направление вращения катушки, а, следовательно, и направления скоростей точек В и О, определяются направлением вектора скорости 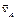 по отношению к МЦС. по отношению к МЦС.
Пример 2. Стержень АВ имеет на концах ползуны, один из которых А скользит по прямолинейной направляющей со скоростью  = = 1 м/с. = = 1 м/с.
Найти в положении, указанном на рис. 4.6, угловую скорость стержня, скорости точек В и С, если АВ = 1, 2 м, АС = ВС.
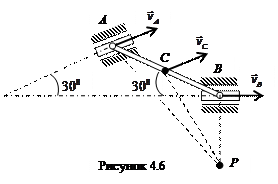
Решение
Стержень АВ совершает плоскопараллельное движение. Так как скорости точек А и В направлены параллельно соответствующим направляющим, вдоль которых скользят ползуны, то, восстанавливая из точек А и В перпендикуляры к скоростям этих точек, определим положение мгновенного центра скоростей стержня АВ – точка Р. Треугольник АВР является равнобедренным, следовательно, АВ = ВР = 1, 2м.
Скорость точки А пропорциональна расстоянию от этой точки до точки Р:  , где , где 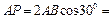 2, 08 м. 2, 08 м.
Вычислим угловую скорость стержня АВ
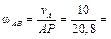 0, 48 рад/с. 0, 48 рад/с.
Скорость точки В определим по формуле
 = 0, 48·1, 2 = 0, 58 м/с. = 0, 48·1, 2 = 0, 58 м/с.
Для определения скорости точки С найдем расстояние РС с помощью теоремы косинусов
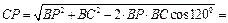 1, 59 м. 1, 59 м.
Тогда скорость точки С
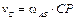 = 0, 76 м/с. = 0, 76 м/с.
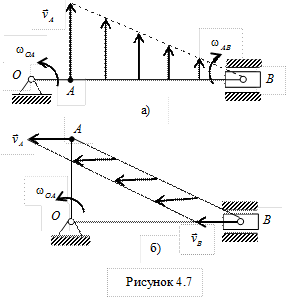
Пример 3. Кривошип ОА длиной r = 1 м вращается с угловой скоростью 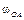 = 2 рад/с, приводя в движение шатун АВ длиной l = 4 м, как показано на рис. 4.7. = 2 рад/с, приводя в движение шатун АВ длиной l = 4 м, как показано на рис. 4.7.
Определить скорость ползуна В, угловую скорость шатуна  в двух положениях механизма, когда угол поворота кривошипа j = 0 и j = 900. в двух положениях механизма, когда угол поворота кривошипа j = 0 и j = 900.
Решение
Шатун АВ совершает плоскопараллельное движение. При этом 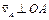 , так как точка А принадлежит кривошипу ОА, совершающему вращательное движение. Скорость ползуна В параллельна направляющим. Численное значение скорости точки А , так как точка А принадлежит кривошипу ОА, совершающему вращательное движение. Скорость ползуна В параллельна направляющим. Численное значение скорости точки А
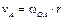 =2·1=2 м/с. =2·1=2 м/с.
Найдем положение мгновенного центра скоростей, восстанавливая перпендикуляры к скоростям точек А и В из этих точек. При угле j = 0 (см. рис. 4.7, а) перпендикуляр к скорости 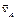 и перпендикуляр к направлению и перпендикуляр к направлению 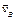 пересекаются в точке В. Следовательно, точка В является в этом положении механизма мгновенным центром скоростей и пересекаются в точке В. Следовательно, точка В является в этом положении механизма мгновенным центром скоростей и 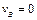 . Это положение механизма называют «мертвым». Найдем угловую скорость шатуна . Это положение механизма называют «мертвым». Найдем угловую скорость шатуна
 = 0, 5 рад/с. = 0, 5 рад/с.
На рис. 4.7, а показано распределение скоростей точек шатуна.
При угле поворота кривошипа j = 900 скорости 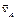 и и 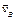 направлены параллельно, а перпендикуляры к ним пересекаются в бесконечности. Следовательно, в данный момент времени имеет место мгновенное поступательное распределение скоростей, то есть все точки шатуна АВ имеют одинаковые скорости, равные направлены параллельно, а перпендикуляры к ним пересекаются в бесконечности. Следовательно, в данный момент времени имеет место мгновенное поступательное распределение скоростей, то есть все точки шатуна АВ имеют одинаковые скорости, равные 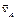 , при этом угловая скорость шатуна wAB = 0 (рис. 4.7, б). , при этом угловая скорость шатуна wAB = 0 (рис. 4.7, б).
Пример 4. Кривошип ОА = 0, 5м вращается с угловой скоростью w 0А = 10 рад/с и приводит в движение шатун АВ = 4 м.
Найти угловую скорость шатуна, скорости точек В и С (АС = 2, 5м), если угол поворота кривошипа j = 450 и ОА ^ АВ (рис. 4.8).
Решение
Так как кривошип ОА совершает вращательное движение, то
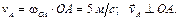
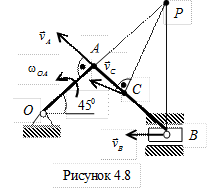 Шатун АВ совершает плоскопараллельное движение. Найдем мгновенный центр скоростей для данного положения шатуна – точку Р на пересечении перпендикуляров к скоростям точек А и В, восстановленных из этих точек. Треугольник РАВ равнобедренный, при этом АВ = АР = 4 м. Шатун АВ совершает плоскопараллельное движение. Найдем мгновенный центр скоростей для данного положения шатуна – точку Р на пересечении перпендикуляров к скоростям точек А и В, восстановленных из этих точек. Треугольник РАВ равнобедренный, при этом АВ = АР = 4 м.
Найдем угловую скорость шатуна АВ
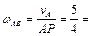 1.25 рад/с. 1.25 рад/с.
Скорости точек В и С пропорциональны их расстояниям до МЦС:
 , ,
где ВР = 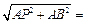 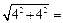 5, 65 м; 5, 65 м;
 = 1, 25·5, 65 = 7, 07 м/с; = 1, 25·5, 65 = 7, 07 м/с;
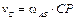 , где СР = , где СР =  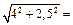 4, 72 м; 4, 72 м;
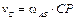 = 1, 25·4, 72 = 5, 9 м/с. = 1, 25·4, 72 = 5, 9 м/с.
4.3.2. Условие и варианты задания К3
Для тела, совершающего плоскопараллельное движение, в соответствии с заданными кинематическими характеристиками и геометрическими размерами элементов, определить угловые скорости и линейные скорости точек. Расчетные схемы и исходные данные приведены в табл. 4.5.
Таблица 4.5
| Вариант К3-1
| | 1.1
| 1.2
| 
| 
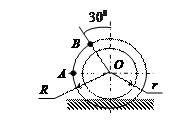
| Катушка катится без скольжения по прямолинейному пути.
Найти угловую скорость катушки, скорости точек А и В, если в рассматриваемый момент
r = 3 см, R = 4 см, 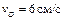 . . 
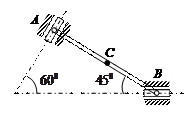
| Стержень АВ имеет на концах ползуны, один из которых А скользит по прямолинейной направляющей со скоростью 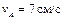 .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 6 см, АС = ВС. .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 6 см, АС = ВС.
| | Вариант К3-2
| | 2.1
| 2.2
| 
| 
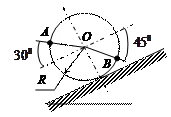
| Колесо катится без скольжения в вертикальной плоскости по наклонному пути.
Найти угловую скорость колеса, скорости точек О и В, если в рассматриваемый момент
R = 2 см, 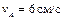 . . 
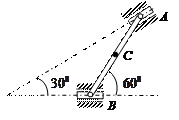
| Стержень АВ имеет на концах ползуны, один из которых А скользит по прямолинейной направляющей со скоростью 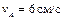 .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 12 см, АС = ВС. .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 12 см, АС = ВС.
| Продолжение табл. 4.5
| Вариант К3-3
| | 3.1
| 3.2
| 
| 
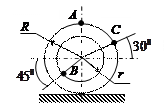
| Катушка катится без скольжения по прямолинейному пути.
Найти угловую скорость катушки, скорости точек В и С, если в рассматриваемый момент
r = 1 см, R = 2 см, 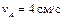 . . 
| Стержень АВ имеет на концах ползуны, один из которых А скользит по прямолинейной направляющей со скоростью 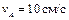 .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 8 см, АС = ВС. .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 8 см, АС = ВС.
| | Вариант К3-4
| | 4.1
| 4.2
| 
| 
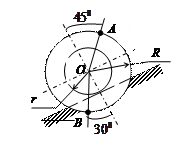
| Катушка катится без скольжения в вертикальной плоскости по наклонному пути.
Найти угловую скорость катушки, скорости точек О и В, если в рассматриваемый момент
r = 4 см, R = 10 см, 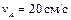 . . 
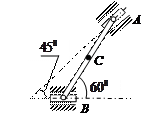
| Стержень АВ имеет на концах ползуны, один из которых А скользит по прямолинейной направляющей со скоростью 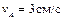 .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 4 см, АС = ВС. .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 4 см, АС = ВС.
| Продолжение табл. 4.5
| Вариант К3-5
| | 5.1
| 5.2
| 
| 
| Катушка катится без скольжения прямолинейному пути.
Найти угловую скорость катушки, скорости точек О и В, если в рассматриваемый момент
r = 5 см, R = 10 см, 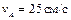 . . 
| Стержень АВ имеет на концах ползуны, один из которых А скользит по прямолинейной направляющей со скоростью 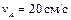 .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 10 см, АС = 6 см. .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 10 см, АС = 6 см.
| | Вариант К3-6
| | 6.1
| 6.2
| 
| 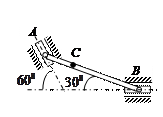
| Катушка катится без скольжения в вертикальной плоскости по наклонному пути.
Найти угловую скорость катушки, скорости точек О и В, если в рассматриваемый момент
r = 2 см, R = 6 см,  . .
| Стержень АВ имеет на концах ползуны, один из которых А скользит по прямолинейной направляющей со скоростью  .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 6 см, АС = 2 см. .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 6 см, АС = 2 см.
|
Продолжение табл. 4.5
| Вариант КЗ-7
| | 7.1
| 7.2
| 
| 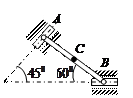
| Колесо катится без скольжения по прямолинейному пути.
Найти угловую скорость колеса, скорости точек О и В, если в рассматриваемый момент
R = 3 см,  = 12 см/с. = 12 см/с.
| Стержень АВ имеет на концах ползуны, один из которых А скользит по прямолинейной направляющей со скоростью
 = 16 см/с.
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 8 см, АС = ВС. = 16 см/с.
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 8 см, АС = ВС.
| | Вариант КЗ-8
| | 8.1
| 8.2
| 
| 
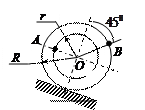
| Катушка катится без скольжения в вертикальной плоскости по наклонному пути.
Найти угловую скорость катушки, скорости точек А и В, если в рассматриваемый момент
R = 4 см, r = 3 см, 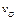 = 10 см/с. = 10 см/с.
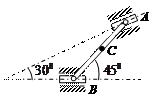
| Стержень АВ имеет на концах ползуны, один из которых А скользит по прямолинейной направляющей со скоростью
 = 20 см/с.
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 10 см, АС = ВС. = 20 см/с.
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 10 см, АС = ВС.
| Продолжение табл. 4.5
| Вариант КЗ-9
| | 9.1
| 9.2
| 
| 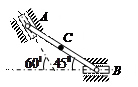
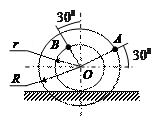
| Катушка катится без скольжения по наклонному пути.
Найти угловую скорость катушки, скорости точек А и В, если в рассматриваемый момент
R = 4 см, r = 2 см,  = 8 см/с. = 8 см/с.
| Стержень АВ имеет на концах ползуны, один из которых А скользит по прямолинейной направляющей со скоростью 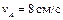 .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 6 см, АС = ВС. .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 6 см, АС = ВС.
| | Вариант КЗ-10
| | 10.1
| 10.2
| 
|  
| Катушка катится без сколь-жения в вертикальной плоскости по наклонному пути.
Найти угловую скорость катушки, скорости точек В и С, если в рассматриваемый момент
R = 4 см, r = 3 см,  = 7 см/с. = 7 см/с.
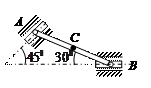
| Стержень АВ имеет на концах ползуны, один из них А скользит по прямолинейной направляющей со скоростью 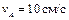 .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 4 см, АС = ВС. .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 4 см, АС = ВС.
| Продолжение табл. 4.5
| Вариант КЗ-11
| | 11.1
| 11.2
| 
| 
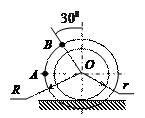
| Колесо катится без скольжения по прямолинейному пути.
Найти угловую скорость колеса, скорости точек О и В, если в рассматриваемый момент
R = 5 см, r = 3 см,  = 12 см/с. = 12 см/с.
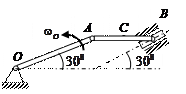
| Кривошип ОА длиной 1 м вращается с угловой скоростью 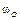 = 2 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость = 2 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость 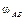 шатуна, скорости точек А и С, если АС = ВС. шатуна, скорости точек А и С, если АС = ВС.
| | Вариант КЗ-12
| | 12.1
| 12.2
| 
| 
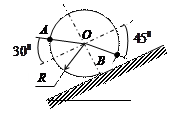
| Катушка катится без сколь-жения в вертикальной плоскости по наклонному пути.
Найти угловую скорость катушки, скорости точек А и В, если в рассматриваемый момент
R = 4 см, 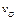 = 10 см/с. = 10 см/с.
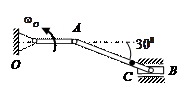
| Кривошип ОА длиной 0, 5 м вращается с угловой скоростью 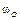 = 2 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость = 2 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость 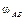 шатуна, скорости точек А и С, если ВС = 0, 2 м. шатуна, скорости точек А и С, если ВС = 0, 2 м.
|
Продолжение табл. 4.5
| Вариант К3-13
| | 13.1
| 13.2
| 
| 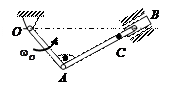
| Катушка катится без скольжения по прямолинейному пути.
Найти угловую скорость катушки, скорости точек А и В, если в рассматриваемый момент
r = 2 см, R = 4 см, 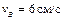 . . 
| Кривошип ОА длиной 0, 5 м вращается с угловой скоростью 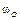 = 3 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость = 3 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость 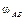 шатуна, скорости точек В и С, если ВС = 0, 1 м. шатуна, скорости точек В и С, если ВС = 0, 1 м.
| | Вариант К3-14
| | 14.1
| 14.2
| 
| 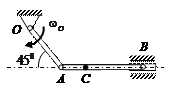
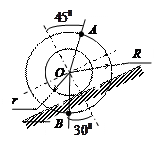
| Катушка катится без скольжения по прямолинейному пути.
Найти угловую скорость катушки, скорости точек А и В, если в рассматриваемый момент
r = 2 см, R = 4 см, 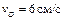 . . 
| Кривошип ОА длиной 0, 4 м вращается с угловой скоростью 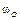 = 2, 5 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость = 2, 5 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость 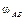 шатуна, скорости точек В и С, если АС = 0, 3 м. шатуна, скорости точек В и С, если АС = 0, 3 м.
|
Продолжение табл. 4.5
| Вариант К3-15
| | 15.1
| 15.2
| 
| 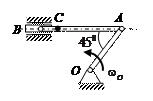
| Катушка катится без скольжения по прямолинейному пути.
Найти угловую скорость катушки, скорости точек А и В, если в рассматриваемый момент
r = 5 см, R = 10 см, 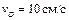 . . 
| Кривошип ОА длиной 0, 6 м вращается с угловой скоростью 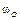 = 2 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость = 2 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость 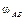 шатуна, скорости точек В и С, если ВС = 0, 3 м. шатуна, скорости точек В и С, если ВС = 0, 3 м.
| | Вариант К3-16
| | 16.1
| 16.2
| 
| 
| Катушка катится без скольжения по прямолинейному пути.
Найти угловую скорость катушки, скорости точек А и В, если в рассматриваемый момент
r = 5 см, R = 10 см, 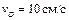 . . 
| Кривошип ОА длиной 0, 4 м вращается с угловой скоростью 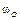 = 1 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость = 1 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость 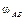 шатуна, скорости точек В и С, если АС = 0, 2 м. шатуна, скорости точек В и С, если АС = 0, 2 м.
|
Продолжение табл. 4.5
| Вариант К3-17
| | 17.1
| 17.2
| 
| 
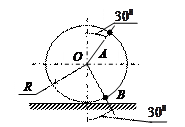
| Катушка катится без скольжения по прямолинейному пути.
Найти угловую скорость катушки, скорости точек А и В, если в рассматриваемый момент
R = 3 см, 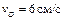 . . 
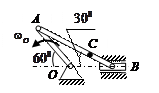
| Кривошип ОА длиной 1 м вращается с угловой скоростью 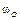 = 1 рад/с и приводит в движение шатун АВ длиной 3 м.
Найти угловую скорость = 1 рад/с и приводит в движение шатун АВ длиной 3 м.
Найти угловую скорость 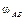 шатуна, скорости точек В и С, если ВС = 1 м. шатуна, скорости точек В и С, если ВС = 1 м.
| | Вариант К3-18
| | 18.1
| 18.2
| 
| 
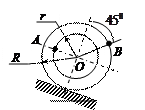
| Катушка катится без скольжения по прямолинейному пути.
Найти угловую скорость ка-тушки, скорости точек А и В, если в рассматриваемый момент
r = 3 см, R = 4 см, 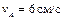 . . 
| Кривошип ОА длиной 1, 5 м вращается с угловой скоростью 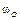 = 2 рад/с и приводит в движение шатун АВ длиной 2 м.
Найти угловую скорость = 2 рад/с и приводит в движение шатун АВ длиной 2 м.
Найти угловую скорость 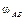 шатуна, скорости точек В и С, если ВС = 0, 15м. шатуна, скорости точек В и С, если ВС = 0, 15м.
|
Продолжение табл. 4.5
| Вариант К3-19
| | 19.1
| 19.2
| 
| 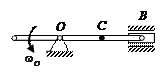
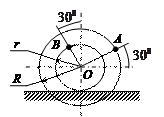
| Катушка катится без скольжения по прямолинейному пути.
Найти угловую скорость катушки, скорости точек А и В, если в рассматриваемый момент
r = 2 см, R = 4 см, 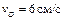 . . 
| Кривошип ОА длиной 0, 5 м вращается с угловой скоростью 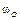 = 2 рад/с и приводит в движение шатун АВ длиной 4 м.
Найти угловую скорость = 2 рад/с и приводит в движение шатун АВ длиной 4 м.
Найти угловую скорость 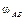 шатуна, скорости точек В и С, если АС = 2, 5 м. шатуна, скорости точек В и С, если АС = 2, 5 м.
| | Вариант К3-20
| | 20.1
| 20.2
| 
| 
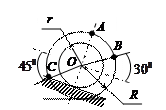
| Катушка катится без скольжения по прямолинейному пути.
Найти угловую скорость катушки, скорости точек А и В, если в рассматриваемый момент
r = 2 см, R = 5 см, 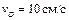 . . 
| Кривошип ОА длиной 0, 5 м вращается с угловой скоростью 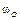 = 1 рад/с и приводит в движение шатун АВ длиной 4 м.
Найти угловую скорость = 1 рад/с и приводит в движение шатун АВ длиной 4 м.
Найти угловую скорость 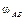 шатуна, скорости точек В и С, если ВС = 1 м. шатуна, скорости точек В и С, если ВС = 1 м.
|
Продолжение табл. 4.5
| Вариант К3-21
| | 21.1
| 21.2
| 
| 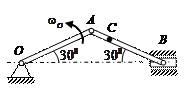
| Катушка катится без скольжения по прямолинейному пути.
Найти угловую скорость катушки, скорости точек А и В, если в рассматриваемый момент
r = 2 см, R = 4 см, 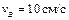 . . 
| Кривошип ОА длиной 2 м вращается с угловой скоростью 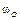 = 2 рад/с и приводит в движение шатун АВ длиной 2 м.
Найти угловую скорость = 2 рад/с и приводит в движение шатун АВ длиной 2 м.
Найти угловую скорость 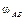 шатуна, скорости точек В и С, если АС = 0, 5 м. шатуна, скорости точек В и С, если АС = 0, 5 м.
| | Вариант К3-22
| | 22.1
| 22.2
| 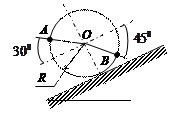
| 
| Катушка катится без скольжения по прямолинейному пути.
Найти угловую скорость катушки, скорости точек А и В, если в рассматриваемый момент, R = 3 см, 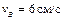 . . 
| Кривошип ОА длиной 2 м вращается с угловой скоростью 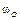 = 2 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость = 2 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость 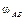 шатуна, скорости точек В и С, если АС = 0, 5 м. шатуна, скорости точек В и С, если АС = 0, 5 м.
|
Продолжение табл. 4.5
| Вариант К3-23
| | 23.1
| 23.2
| 
| 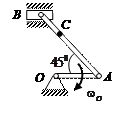
| Катушка катится без скольжения по прямолинейному пути.
Найти угловую скорость катушки, скорости точек А и В, если в рассматриваемый момент
r = 3 см, R = 4 см,  . . 
| Кривошип ОА длиной 1 м вращается с угловой скоростью 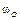 = 2 рад/с и приводит в движение шатун АВ длиной 3 м.
Найти угловую скорость = 2 рад/с и приводит в движение шатун АВ длиной 3 м.
Найти угловую скорость 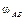 шатуна, скорости точек В и С, если ВС = 1 м. шатуна, скорости точек В и С, если ВС = 1 м.
| | Вариант К3-24
| | 24.1
| 24.2
| 
| 
| Катушка катится без скольжения по прямолинейному пути.
Найти угловую скорость катушки, скорости точек А и В, если в рассматриваемый момент
r = 3 см, R = 6 см,  . . 
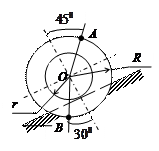
| Стержень ОА длиной 1 м шарнирного четырехзвенника вращается с угловой скоростью 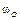 = = 2 рад/с. длиной 1 м.
Найти угловые скорости стержней АВ длиной 2 м и ВD длиной 3 м, а также скорости точек В и С, если АС = 1 м. = = 2 рад/с. длиной 1 м.
Найти угловые скорости стержней АВ длиной 2 м и ВD длиной 3 м, а также скорости точек В и С, если АС = 1 м.
| | | | | |
СПИСОК РЕКОМЕНДУЕМОЙ ЛитературЫ
1. Тарг С.М. Краткий курс теоретической механики.– М.: Высшая школа, 1974.– 400 с.
2. Бутенин И.В., Лунц Я.Л., Меркин Д.Р. Краткий курс теоретической механики. Т.1: Статика и кинематика.– М.: Наука, 1985.– 240 с.
3. Яблонский А.А. Курс теоретической механики Ч.1: Статика. Кинематика.– М.: Высшая школа, 1984.– 343 с.
4. Павловський М.А. Теоретична механіка.– Київ: Техніка, 2002.– 670 с.
5. Беломытцев А.С. Краткий курс теоретической механики. Статика и кинематика / Тексты лекций для студентов заочной формы обучения всех специальностей.– Харьков: НТУ «ХПИ», 2004.– 76 с.
6. Адашевский В.М., Анищенко Г.О., Тарсис Ю.Л. Общий курс теоретической механики / Учебное пособие для студентов заочной формы обучения.– Харьков: НТУ «ХПИ», 2005.– 108 с.
7. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Т.1: Статика и кинематика.– М.: Наука, 1990.– 670 с.
СОДЕРЖАНИЕ
| Введение............................................
|
| | 1. Кинематика точки..................................
|
| | 1.1. Способы задания движения точки...................
|
| | 1.2. Скорость точки...................................
|
| | 1.3. Ускорение точки..................................
|
| | 1.4. Частные случаи движения точки....................
|
| | Вопросы для самоконтроля............................
|
| | 2. Кинематика твердого тела...........................
|
| | 2.1. Понятие о степенях свободы твердого тела...........
|
| | 2.2. Поступательное движение тела.....................
|
| | 2.3. Вращение твердого тела вокруг неподвижной оси.....
|
| | 2.4. Преобразование простейших движений..............
|
| | Вопросы для самоконтроля............................
|
| | 3. Плоскопараллельное движение твердого тела..........
|
| | 3.1. Уравнения плоскопараллельного движения. Разложение движения на поступательное и вращательное.............
|
| | 3.2. Определение скоростей и ускорений точек тела.......
|
| | 3.3. Мгновенный центр скоростей......................
|
| | Вопросы для самоконтроля............................
|
| | 4. Задания к контрольным работам......................
|
| | 4.1. Определение скорости и ускорения точки по заданным уравнениям ее движения. Задание К1...................
|
| | 4.1.1. Пример решения контрольного задания К1..........
|
| | 4.1.2. Условия и варианты задания К1...................
|
| | 4.2. Преобразование простейших движений твердого тела. Задание К2..........................................
|
| | 4.2.1. Пример решения контрольного задания К2..........
|
| | 4.2.2. Условия и варианты задания К2...................
|
| | 4.3. Определение скоростей точек тела при
плоскопараллельном движении. Задание К3..............
|
| | 4.3.1. Примеры решения контрольного задания К3........
|
| | 4.3.2. Условия и варианты задания К3...................
|
| | Список рекомендуемой литературы....................
|
|
Навчальне видання
АДАШЕВСЬКИЙ Володимир Михайлович
АНІЩЕНКО Галина Оттівна
ТАРСІС Юрій Львович
ТЕОРЕТИЧНА МЕХАНІКА.
КІНЕМАТИКА
Навчально-методичний посібник
для студентів заочної форми навчання усіх спеціальностей
Російською мовою
Роботу до друку рекомендував Д.В. Бреславський
В авторській редакції
Комп’ютерна верстка та графічне оформлення – І.Р. Грабовська
План 2007, п. 42/
Підп. до друку..07. Формат 60х84 1/16. Папір офсет. № 2.
Riso – друк. Гарнітура Таймс. Ум. друк. арк. 2, 8. Обл.-вид. арк. 4, 5.
Наклад 100 прим. Зам. №. Ціна договірна
Видавничий центр НТУ «ХПІ».
Свідоцтво про державну реєстрацію ДК № 116 від 10.07.2000 р.
61002, Харків, вул. Фрунзе, 21
______________________________________________________________
Друкарня НТУ «ХПІ».61002, Харків, вул. Фрунзе, 21

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Тема: Изучение приспособленности организмов к среде обитания Цель:выяснить механизм образования приспособлений к среде обитания и их относительный характер, сделать вывод о том, что приспособленность – результат действия естественного отбора...
Тема: Изучение фенотипов местных сортов растений Цель: расширить знания о задачах современной селекции. Оборудование:пакетики семян различных сортов томатов...
Тема: Составление цепи питания Цель: расширить знания о биотических факторах среды. Оборудование:гербарные растения...
|
Закон Гука при растяжении и сжатии
Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука, по имени установившего этот закон английского физика Роберта Гука в 1678 году...
Характерные черты официально-делового стиля Наиболее характерными чертами официально-делового стиля являются:
• лаконичность...
Этапы и алгоритм решения педагогической задачи Технология решения педагогической задачи, так же как и любая другая педагогическая технология должна соответствовать критериям концептуальности, системности, эффективности и воспроизводимости...
|
|

 Найти угловую скорость катушки, скорости точек О и В, если в рассматриваемый момент времени
Найти угловую скорость катушки, скорости точек О и В, если в рассматриваемый момент времени  = 2 м/с,
= 2 м/с,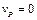 , следовательно эта точка является мгновенным центром скоростей (МЦС). Вектор скорости точки А
, следовательно эта точка является мгновенным центром скоростей (МЦС). Вектор скорости точки А 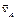 перпендикулярен АР и направлен в сторону качения катушки, а численное значение скорости пропорционально расстоянию от точки А до МЦС:
перпендикулярен АР и направлен в сторону качения катушки, а численное значение скорости пропорционально расстоянию от точки А до МЦС: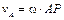 ,
,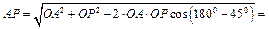
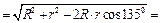 1, 49 м.
1, 49 м.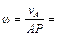 1, 35 рад/с.
1, 35 рад/с.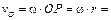 0, 81 м/с;
0, 81 м/с;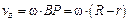 = 0, 54 м/с.
= 0, 54 м/с.
 , где
, где 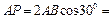 2, 08 м.
2, 08 м.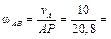 0, 48 рад/с.
0, 48 рад/с. = 0, 48·1, 2 = 0, 58 м/с.
= 0, 48·1, 2 = 0, 58 м/с.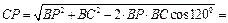 1, 59 м.
1, 59 м.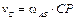 = 0, 76 м/с.
= 0, 76 м/с.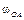 = 2 рад/с, приводя в движение шатун АВ длиной l = 4 м, как показано на рис. 4.7.
= 2 рад/с, приводя в движение шатун АВ длиной l = 4 м, как показано на рис. 4.7.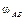 в двух положениях механизма, когда угол поворота кривошипа j = 0 и j = 900.
в двух положениях механизма, когда угол поворота кривошипа j = 0 и j = 900.
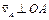 , так как точка А принадлежит кривошипу ОА, совершающему вращательное движение. Скорость ползуна В параллельна направляющим. Численное значение скорости точки А
, так как точка А принадлежит кривошипу ОА, совершающему вращательное движение. Скорость ползуна В параллельна направляющим. Численное значение скорости точки А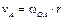 =2·1=2 м/с.
=2·1=2 м/с.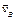 пересекаются в точке В. Следовательно, точка В является в этом положении механизма мгновенным центром скоростей и
пересекаются в точке В. Следовательно, точка В является в этом положении механизма мгновенным центром скоростей и 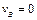 . Это положение механизма называют «мертвым». Найдем угловую скорость шатуна
. Это положение механизма называют «мертвым». Найдем угловую скорость шатуна = 0, 5 рад/с.
= 0, 5 рад/с.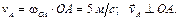
 Шатун АВ совершает плоскопараллельное движение. Найдем мгновенный центр скоростей для данного положения шатуна – точку Р на пересечении перпендикуляров к скоростям точек А и В, восстановленных из этих точек. Треугольник РАВ равнобедренный, при этом АВ = АР = 4 м.
Шатун АВ совершает плоскопараллельное движение. Найдем мгновенный центр скоростей для данного положения шатуна – точку Р на пересечении перпендикуляров к скоростям точек А и В, восстановленных из этих точек. Треугольник РАВ равнобедренный, при этом АВ = АР = 4 м.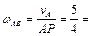 1.25 рад/с.
1.25 рад/с.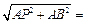
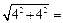 5, 65 м;
5, 65 м;
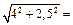 4, 72 м;
4, 72 м;

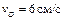 .
. 
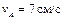 .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 6 см, АС = ВС.
.
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 6 см, АС = ВС.


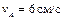 .
. 

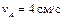 .
. 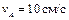 .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 8 см, АС = ВС.
.
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 8 см, АС = ВС.


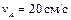 .
. 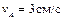 .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 4 см, АС = ВС.
.
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 4 см, АС = ВС.


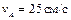 .
. 
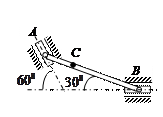
 .
.




 = 10 см/с.
= 10 см/с.

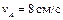 .
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 6 см, АС = ВС.
.
Найти в положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С, если АВ = 6 см, АС = ВС.





 = 2 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость
= 2 рад/с и приводит в движение шатун АВ длиной 1 м.
Найти угловую скорость 



 .
. 
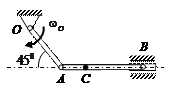

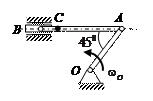
 .
. 






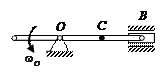


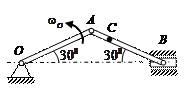
 .
. 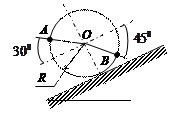


 .
. 

 .
. 


