Введение 5
1 Цель и задачи лабораторной работы 6 1.1 Цель работы 6 1.2 Задачи работы6 2. Содержание лабораторной работы 7 2.1 Теоретическая часть 7 2.2 Практическая часть 9 3 Оборудование 10 3.1Оборудование для выполнения лабораторной работы 10 4 Учебная и нормативная литература 12 4.1Учебная литература 12 4.2 Нормативная литература 12 5 Меры безопасности на рабочем месте 13 5.1 Общие требования безопасности 13 5.2 Требования безопасности во время работы 13 6 Рекомендации студентам по выполнению лабораторной работы 14 6.1 Условия и организация работы 14 6.2 Последовательность и технология выполнения работы15 7 Вопросы для самоконтроля 16 7.1 Вопросы по теоретической части 16 7.2 Вопросы по практической части 16 Бланк отчёта о лабораторной работе 17 Приложение А Формулы для определения площадей простых геометрических фигур 20 Большое практическое значение имеет определение центра тяжести различных машин и механизмов. В методических указаниях рассматривается последовательность выполнения лабораторной работы. Данные методические указания направлены на то, чтобы закрепить полученные студентами знания по расчёту центра тяжести сложных плоских фигур и научить их применять полученные знания на практике при расчёте центра тяжести представленных лабораторных образцов. Методические указания к лабораторным работам являются результатом развития системы проведения лабораторных работ в колледже и позволяют студентам проявить большую самостоятельность и возможность лучшего усвоения ими нового материала.
1 Цель и задачи лабораторной работы 1.1 Цель работы Определить центр тяжести сложной плоской фигуры опытным путём (методом подвешивания) и сравнить полученные данные с расчётными.
1.2 Задачи работы:
- знать методы для определения центра тяжести тела; - уметь определять положения центра тяжести простых и сложных геометрических фигур; - уметь определять статические моменты площади.
Содержание лабораторной работы 2.1 Теоретическая часть
Центр тяжести это геометрическая точка, которая может быть расположена и вне тела (диск с отверстием, полый шар и т. д.). На практике большое значение имеет определение центра тяжести тонких плоских однородных пластин. Их толщиной можно пренебречь и считать, что центр тяжести расположен в плоскости. Если координатную плоскость ХОУ совместить с плоскостью фигуры, то положение центра тяжести определяется двумя координатами. Координаты центра тяжести плоской фигуры x c и y c, мм, определяют по формулам
где
А – площадь фигуры, мм2. Статические моменты площади плоской фигуры S х, S у, мм3, определяют по формулам
где
При решении задач используются следующие методы: - метод симметрии: центр тяжести симметричных фигур находится на оси симметрии; - метод разделения: сложные сечения разделяем на несколько простых частей, положение центров тяжести которых легко определить; - метод отрицательных площадей: полости (отверстия) рассматриваются как часть сечения с отрицательной площадью. Положения центров тяжести простых геометрических фигур определяются в соответствии с рисунком 2.1.
Рисунок 2.1 2.2 Практическая часть:
- определение центра тяжести сложной плоской фигуры опытным путём (методом подвешивания); - определение центра тяжести сложной плоской фигуры аналитическим путём (методом расчётов); - сравнить опытные данные с расчётными; - заполнение бланка отчёта и защита работы.
|

 , (2.1)
, (2.1)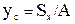 , (2.2)
, (2.2)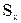 – статический момент площади относительно оси Х, мм3;
– статический момент площади относительно оси Х, мм3; – статический момент площади относительно оси У, мм3
– статический момент площади относительно оси У, мм3 , (2.3)
, (2.3) , (2.4)
, (2.4) – площадь части фигуры, мм2 (формулы для определения площадей в приложении А);
– площадь части фигуры, мм2 (формулы для определения площадей в приложении А); - координаты центра тяжести частей фигуры, мм.
- координаты центра тяжести частей фигуры, мм.






