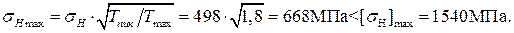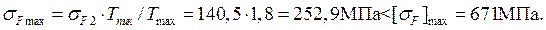Проверочный расчет передачи по контактным напряжениям
По формуле (8.43) контактные напряжения
где Т1=Твх= 132× 103 Н·мм; U=Uконф= 1, 89. По таблице 4.10 Приложения с понижением степени точности на одну степень находим КHV=1, 08, KHb=1, 026. Тогда KH= KHb × КHV = 1, 026× 1, 08 = 1, 1, а
Недогруз составил
что меньше допускаемых 10%. Следовательно, контактная прочность обеспечена. Окончательно принимаем b= 35, 5 мм. Проверочный расчёт передачи по напряжениям изгиба По формуле (8.40) напряжения изгиба sF=(YFS ·Ft·KF)/(nF·b·mm)£ [sF], где nF = 0, 85 – опытный коэффициент, характеризующий понижение прочности конической прямозубой передачи по сравнению с цилиндрической; коэффициент формы зуба YFS определится по рисунку 4.3 Приложения в соответствии с эквивалентным числом зубьев ZV и коэффициентом смещения x. Определяем ZV1=Z1/cos d1= 37/cos27, 88° = 41, 8; ZV2=Z2/cos d2= 70 / cos62, 12° = 150. По формуле (8.50) назначаем коэффициент смещения для шестерни x1=2·(1-1/U2кон ф)· Коэффициент смещения для колеса (см. с. 158) x2=-x1= - 0, 2. В результате получаем соответственно значения YFS1= 3, 58 и YFS2= 3, 62. Коэффициент нагрузки при изгибе KF=KFb·KFV. По таблице 4.10 Приложения с понижением степени точности на одну степень определяем коэффициент динамической нагрузки при изгибе KFV= 1, 2. При ранее найденном значении KHb=1, 026 определяем (см. с. 156) величину KFb=1+(KHb-1)·1, 5= 1+(1, 026 – 1) × 1, 5 = 1, 039. Получаем, что KF= 1, 039 × 1, 2 = 1, 25. Сравниваем значения [sF]1/YFS1=278/3, 58=77, 7 МПа и [sF]2/YFS2 =252/3, 62 = 69, 6 МПа. Дальнейший расчёт ведём по колесу (меньшему значению). В результате расчетное напряжение изгиба sF=sF2=(3, 62× 2530× 1, 25/(0, 85× 35, 5× 2, 7)= 140, 5 МПа < [sF]2= 252 МПа, т.е. условие прочности соблюдается. Примечание. Если sF> [sF] более, чем на 5%, то следует увеличить модуль mte, соответственно пересчитать числа зубьев Z1 и Z2 и повторить проверочный расчёт на изгиб. При этом внешний делительный диаметр колеса de2 не изменяется, а, следовательно, не нарушается контактная прочность передачи. Уточняем значения внешних диаметров вершин зубьев шестерни и колеса (таблица 5.6 Приложения): dae1=de1+2·(1+xe1)·mte·cosd1=117 + 2(1+0, 2) × 3, 14 × Cos27, 88° = 120, 3 мм и dae2=dе2+2·(1-xe1)·mte·cosd2= 220 + 2(1-0, 2) × 3, 14 × Cos62, 12° = 221, 2 мм. Вычисляем внешние диаметры впадин зубьев шестерни и колеса (там же): dfе1=de1-2·(1, 2-xе1)·mte·cosd1= 117 - 2(1, 2 - 0, 2) × 3, 14 × Cos27, 88° = 111, 4 мм и dfe2=dе2-2·(1, 2+xe1)·mte·сosd2=220 - 2(1, 2+0, 2) × 3, 14 × Cos62, 12° = 215, 9 мм. Проверочный расчёт зубьев передачи при кратковременных перегрузках По аналогии с расчетом тихоходной ступени максимальные контактные напряжения
Максимальные напряжения изгиба при перегрузках
Таким образом, условия прочности при перегрузках соблюдаются.
|

 ,
,
 ,
,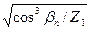 =
=  = 0, 2 (bn=0° для прямозубых передач).
= 0, 2 (bn=0° для прямозубых передач).