Определение геометрических параметров передачи
Внешний делительный диаметр конического колеса
где nН - коэффициент вида конических колёс (для прямозубых nН=0, 85 – с. 154); Т2=Твых, Н·мм; U=Uкон=U ред= 1, 88. Согласно рисунка 5.1б Приложения для кривой " 1р" и (Kbе·U)/(2-Kbе) = =(0, 285 × 1, 88) / (2 – 0, 285) = 0, 31; КНb = 1, 026. Получаем, что Углы делительных конусов: колеса d2=arctg(U)=arctg(1, 88)= 62, 1°; шестерниd1=90°-d2=90°- 62.1°= 27, 9°. Внешнее конусное расстояние Re=de2/(2·sin(d2))= 220/(2·sin(62.1°))= 125 мм. Ширина зубчатого венца шестерни и колеса b=0, 285·Re=0, 285· 125 = 35, 5 мм. Средний делительный диаметр шестерни dm1=de1·(Re-0, 5·b)/Re, где de1=de2/Uкон= 220/ 1, 88 = 117 мм. Получаем, что dm1= 117 × (125 – 0, 5 × 35, 5) / 125 = 100мм. Число зубьев шестерни и колеса По рисунку 5.2а Приложения находим величину Z1¢ =23, и далее, для Н2£ 350 НВ определим по таблице 5.1 Приложения Z1= 1, 6 ·Z1¢ = 1, 6 × 23 = 36, 8. Полученное значение округляем в ближайшую сторону, т.е. Z1= 37. Из условия уменьшения шума и отсутствия подрезания зубьев для прямозубых конических колес рекомендуется принимать Z1³ 18 (таблица 5.5 Приложения). Следовательно, величина Z1= 37 приемлема. Число зубьев колеса Z2=Z1·Uкон= 37 × 1, 88 = 69, 6. Принимаем Z2= 70. Фактическое передаточное число передачи Uкон ф=Z2/Z1= 70 / 37 = 1, 89. Отклонение фактического передаточного числа от расчётного составляет DU=((Uкон ф-Uкон)/Uкон)·100%= ((1, 89 – 1, 88) / 1.88) × 100% = 0, 5%, что меньше допустимых 4%. Если отклонение составит более 4%, необходимо будет скорректировать значения Z1 и Z2. Поскольку Z2 пришлось округлить до целого числа и изменилось U, необходимо уточнить углы d1 и d2: d2=arctg Uкон ф=arctg 1, 89= 62, 12°; d1=90°-d2=90°- 62, 12°= 27, 88°. Модуль в среднем сечении шестерни mtm=dm1/Z1= 100 / 37 = 2, 7 мм. Внешний окружной модуль mte=de2/Z2= 220 / 70 = 3, 14 мм, что больше рекомендуемого минимального значения mte=1, 5 мм. Примечание. Допускается использовать нестандартное значение модуля, так как одной и той же зуборезной головкой можно нарезать конические колеса с модулями, изменяющимися в некотором непрерывном диапазоне. Внешний диаметр вершин (без учёта коэффициента смещения): зубьев шестерни dae1=de1+2·mte·cos d1= 117 + 2× 3, 14× Cos27, 88°= 122, 6 мм; и колеса dae2=de2+2·mte·cos d2= 220 + 2× 3, 14× Cos62, 12° = 223 мм. Проверим пригодность заготовок. Для конической шестерни b=35, 5< S(1)=60 мм и dae1»122, 6> d(1)=120 мм. Для конического колеса b= 35, 5< S(2ср)=100 мм и dae2»223 > d(2ср)=200 мм. Делаем вывод, что изготовление зубчатых колёс конической ступени из стали 40Х с заданными максимальными размерами заготовок невозможно. По таблице 4.1 Приложения делаем замену материала зубчатых колес на сталь 40ХН с той же термообработкой. Для шестерни принимаем S(1)=100 мм и d(1)=200 мм, а для колеса – S(2ср)=200 мм и d(2ср)=400 мм. Эти числа приемлемы, так как в этом случае dae1=122, 6 мм < d(1)=200 мм и dae2=223 мм < d(2ср)=400 мм. Параметры стали 40ХН с указанными допустимыми размерами заготовок очень близки к параметрам стали 40Х с принятыми предварительно размерами заготовок. В связи с этим пересчет передачи (раздел 2.4) производить не будем. Средний делительный диаметр колеса dm2=dm1·Uкон ф= 100 × 1, 89 = 189 мм. Внешний делительный диаметр шестерни de1=de2/Uкон ф= 220 / 1, 89 = 116 мм. Определение усилий в зацеплении (таблица 5.9 Приложения) Окружная сила Ft1=Ft2=2·T2/dm2=2·Tпp/dm2= 2 × Tвых / dm2 = 2 × 239 × 1000 / 189 = 2530 H; радиальная cила на шестерне Fr1 = Ft1·tg a= 2530 × tg20° = 920 Н; осевая сила на шестерне Fa1=Fr1·sin d1= 920 × sin27, 88° = 430 H. Кроме того, осевая сила на колесе Fa2=Fr1, а радиальная сила на колесе Fr2=Fa1.
|

 (формула 8.45)
(формула 8.45)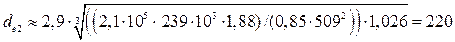 мм.
мм.


