Уравнение неразрывности струиvS = const или v1S1 = v2S2 Произведение величины скорости течения несжимаемой жидкости на величину поперечного сечения трубки тока есть величина постоянная для данной трубки тока При движении жидкостей и газов в них возникают силы внутреннего трения, возникающие между слоями жидкости, испытывающими относительное перемещение. Свойства жидкости, связанные с наличием сил внутреннего трения, называется вязкостью. Модель жидкости, сжимаемостью и вязкостью которой пренебрегают, называется идеальной жидкостью. Всякая реальная жидкость обладает сжимаемостью и вязкостью; для решения задач о движении реальной жидкости гидродинамика пока не имеет общих теоретических методов. При течении жидкости наблюдаются два ее вида течения: а) ламинарное (пластинчатое) – движение жидкости параллельными слоями, не перемешиваясь. б) турбулентное (вихревое) – частицы жидкости движутся по искривленным случайно изменяющимся во времени траекториям. Ламинарное течение – течение стационарное Турбулентное течение – течение нестационарное. Английский учёный Рейнольдс установил, что характер течения зависит от значения безразмерной величины, называемой числом Рейнольдса Re:
где ρ – плотность жидкости (газа); v – средняя скорость потока; ℓ – геометрический размер сечения; η – вязкость. При малых Re – ламинарное течение, при больших – турбулентное. Величина
Рассмотрим стационарное течение идеальной жидкости.
Это уравнение связывает изменение давления с изменением скорости течения и геометрической высотой. Уравнение Бернуллипредставляет собой закон сохранения энергии для единицы объема жидкости:
ρ gh – Еп энергия единицы объема жидкости в поле силы тяжести; Р – работа силы давления при подъеме единицы объема на единицу высоты; ρ – называется статистическим давлением;
Скорость истечения из отверстия - формула Торричелли
|
,
в уравнении (6) называется кинематической вязкостью ν:
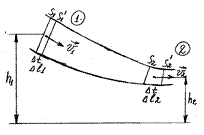
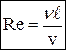
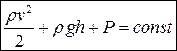– уравнение Бернулли
– Ек энергия единицы объема жидкости;
– называется динамическим давлением.
–
