Классификация и типы грунтовых оснований
Вариант 1 1. Камень бросили под углом к горизонту со скоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет. a) [ ] во всех точках одинаков b) [ ] c) [ ] d) [ ]
2. Теннисный мяч летел с импульсом a) [ 5 Н ] b) [ 0, 5 Н ] c) [ 50 Н ] d) [ 30 Н ] 3.
a) [ 1 ] b) [ 2 ] c) [ 3 ] d) [ 4 ] e) [ 5 ]
Вариант 2 1.
a) [
2. Импульс тела a) [ ] 1 b) [ ] 2 c) [ ] 3 d) [ ] 4
3.
a) [ ] c) [ ]
Вариант 3 . a) [
a) [ b) [ c) [ d) [
3.
a)
1.
a) [
2.
a) [ 2 с ] b) [ 0, 2 с ] c) [ 0, 05 с ] d) [ 0, 5 с ] e) [ 0, 3 с ]
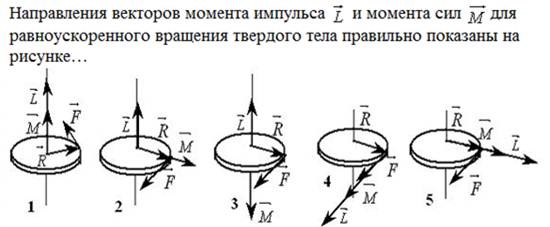
3. Момент импульса тела относительно неподвижной оси изменяется по закону L = ct3. Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело. a)
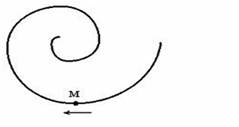
1. Точка М движется по спирали в направлении, указанном стрелкой. Нормальное ускорение по величине не изменяется. При этом величина скорости…
a) [ Увеличивается ] b) [ Уменьшается ] c) [ не изменяется ]
2.
a) [ b) [ c) [ d) [ e) [
3.
a)
1. Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина нормального ускорения...
a) [ уменьшается ] b) [ увеличивается ] c) [ не изменяется ]
. a) [ 1 ] b) [ 2 ] c) [ 3 ] d) [ 4 ]
3.
a)
Точка М движется по спирали с постоянным по величине нормальным ускорением в направлении, укачанном стрелкой. При этом проекция тангенциального ускорения на направление скорости...
a) [ меньше нуля ] b) [ больше нуля ] c) [ равна нулю ] 2.
3. Два маленьких массивных шарика закреплены на концах невесомого стержня длины d. Стержень может вращаться в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Стержень раскрутили до угловой скорости a)
1. Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция тангенциального ускорения на направление скорости положительна, то величина нормального ускорения... a) [ не изменяется ] b) [ увеличивается ] c) [ уменьшается ]
2.
a) [ 1 ] b) [ 2 ] c) [ 3 ] d) [ 8 ]
3.
a)
Материальная точка M движется по окружности со скоростью a) 1 b) 2 c) 3 d) 4
2.
Укажите график, правильно отражающий зависимость угловой скорости диска от времени.
a)
1. Материальная точка M движется по окружности со скоростью a) [ ] 1 b) [ ] 2 c) [ ] 3 d) [ ] 4
2.
a) b) c) d) 3. Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике a) в c) в
1. Колесо вращается так, как показано на рисунке белой стрелкой. К ободу колеса приложена сила, направленная по касательной. Правильно изображает угловую скорость вектор … a) [ ] 1 b) [ ] 2 c) [ ] 3 d) [ ] 4 e) [ ] 5
2.
a) 3. С ледяной горки с небольшим шероховатым участком АС из точки А без начальной скорости скатывается тело. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике a) 120 Дж тепла b) 80 Дж тепла c) 100 Дж тепла d) 60 Дж тепла
1. Колесо вращается так, как показано на рисунке белой стрелкой. К ободу колеса приложена сила, направленная по касательной. Правильно изображает момент импульса колеса относительно заданной оси вектор … b) 2 c) 3 d) 4 e) 5
2.
a)
3. В потенциальном поле сила то зависимость проекции силы a)
1. Частица движется вдоль окружности радиусом 1 м в соответствии с уравнением j(t) = 2p(t2 - 6t +12), где j- в радианах, t - в секундах. Число оборотов, совершенной частицей до остановки, равно … a) [ 1 ] b) [ 6 ] c) [ 3 ] d) [ 2 ]
2. Лифт движется вниз с ускорением а> g, при этом… a) тело будет находиться в невесомости b) с телом ничего не произойдет c) тело прижмется к потолку лифта d) тело прижмется к полу лифта
3.
a) 50 Дж b) 40 Дж c) 25 Дж d) [ ] 20 Дж e) [ ] 15 Дж
1.
a) [
2. Шарик падает вертикально вниз в жидкости. Если на него действуют a) c)
3. Диск и цилиндр имеют одинаковые массы и радиусы (рис.). Для их моментов инерции справедливо соотношение… a) Iц=Iд b) Iц> Iд c) Iц< Iд
1.
a) [
2.
a) c)
3.
a) 1 c b) 2 c c) 3 c d) 4 c
Классификация и типы грунтовых оснований Итак, грунтом называют горные породы, а также твердые отходы производственной и хозяйственной деятельности человека, находящиеся в пределах зоны выветривания земли и являющиеся объектом инженерно-строительной деятельности человека. В соответствии с ГОСТ 25 100 – 95 «Грунты. Классификация» все грунты классифицируются по характеру структурных связей (классы); по происхождению (группы); по условиям образования (подгруппы) по петрографическому и гранулометрическому составу, степени неоднородности и числу пластичности (тип); по структуре, текстуре, составу связующего вещества, плотности сложения, относительному содержанию и степени разложения органических веществ, по степени уплотнения от собственного веса (вид). ГОСТ 25 100 – 95 разделяет все грунты на два класса: грунты с жесткими структурными связями (класс скальных грунтов); грунты без жестких структурных связей (класс нескальных грунтов). В зависимости от предела прочности на одноосное сжатие в водонасыщенном состоянии (Rc) скальные грунты естественного или искусственного происхождения делят на скальные (Rc ≥ 5 МПа) и полускальные (Rc < 5 МПа). Искусственные скальные породы могут быть получены закреплением грунта в природном залегании различными методами: силикатизацией, цементацией, смолизацией, термической обработкой и др. Пески относят к группе обломочных несцементированных грунтов, подгруппе обломочных песчаных. 9 - Строение оснований. Сооружение редко располагается на одном грунте. Обычно в основании залегают несколько типов грунтов (Рисунок 1). Тогда кроме оценки свойств каждого грунта возникает не менее важная задача – схематизация геологического строения основания (это задача курса инженерной геологии). Различают такие понятия как: инженерно-геологические элементы (однородные части в геологической среде); границы между этими элементами; мощность слоя; линза (внутренне однородное геологическое тело, ограниченное в пределах рассматриваемой области замкнутой поверхностью); жила (внутренне однородное геологическое тело, протяженное и пересекающее другие слои); зона (область перехода от грунтов с одними свойствами к грунтам с другими свойствами). Среди грунтов, на которых возводятся сооружения, есть несколько характерных типов особенных образований. Строительство на таких грунтах сопряжено со специальными мероприятиями, несоблюдение которых часто приводит к авариям. К таким грунтам относят мерзлые, вечномерзлые, лессовые, набухающие, слабые водонасыщенные глинистые, засоленные, насыпные грунты, торфы, заторфованные грунты. Эти грунты называют структурно – неустойчивыми грунтами. Грунты всех видов относятся к мерзлым, если они имеют отрицательную температуру и содержат в своем составе лед. Грунты называют вечномерзлыми, если в условиях природного залегания они находятся в мерзлом состоянии непрерывно (без оттаивания) в течение многих лет (трех и более) лет. Мерзлые и вечномерзлые грунты из-за наличия в них льдоцементных связей при отрицательной температуре являются очень прочными и малодеформируемыми природными образованиями. При положительной температуре свойства таких грунтов резко меняются. При оттаивании порового льда структурные льдоцементные связи лавинно разрушаются и возникают значительные деформации. Многие виды вечномерзлых грунтов, особенно сильнольдистые глинистые грунты, при этом могут переходить в разжиженное состояние.
10 - Определение напряжений в массивах грунтов.Основные положения. Распределение напряжений в грунтовой толще зависит от многих факторов. Прежде всего к ним относятся: характер и режим нагружения массива, инженерно – геологические и гидрогеологические особенности площадки строительства, состав и физико – механические свойства грунтов. Формирование напряжений в грунтовой толще происходит не мгновенно при приложении нагрузки, а может развиваться длительное время. Это связано со скоростью протекания деформаций и особенно сильно проявляется в пылевато - глинистых грунтах, где процессы фильтрационной консолидации и ползучести развиваются очень медленно. Под действием собственного веса в массивах грунтов всегда формируется начальное напряженное состояние, оно может осложняться различными геодинамическими процессами. Поэтому напряжения, возникающие в массивах грунтов от действия сооружения, накладываются на уже имеющиеся в нем собственные напряжения. Это приводит к формированию сложного поля напряжений в грунтовой толще. Определение напряжений в грунте - сложная задача, решаемая с помощью линейной теории упругости. Определенное с помощью теории упругости поле напряжений соответствует конечному, стабилизированному, состоянию грунтов. То есть к моменту времени, когда все деформации, вызванные приложением нагрузок, уже совершились. При расчетах оснований и фундаментов сооружений используют расчетные схемы
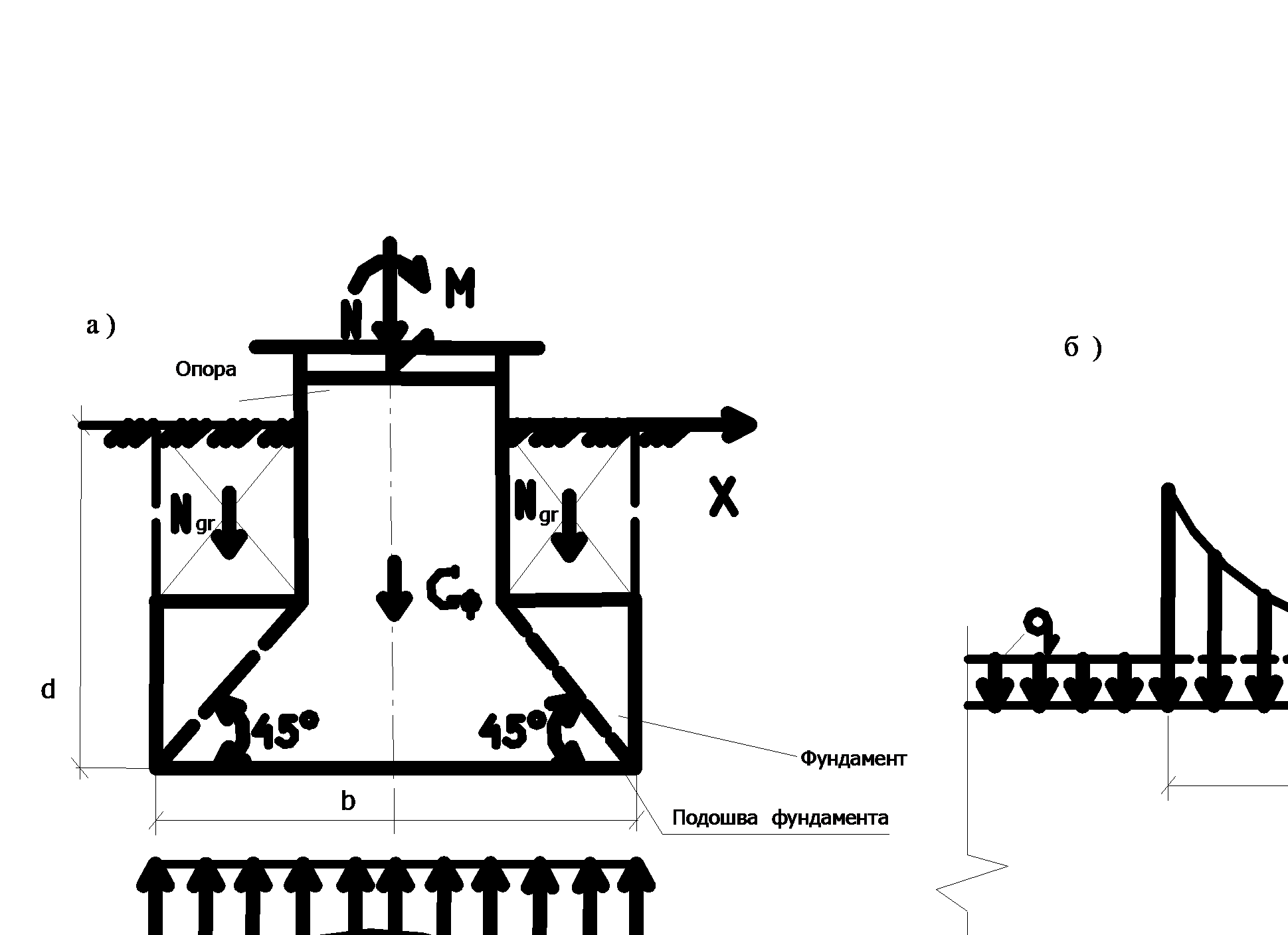
11 - Расчетная схема взаимодействия сооружения и основания. При расчетах оснований и фундаментов сооружений используют расчетные схемы (Рисунок 6, а, б).
Рисунок 6 - Схема фундамента и реактивного напряжения по его подошве: а) схема фундамента и реактивного напряжения по его подошве; б) расчетная схема передачи нагрузок ниже подошвы фундамента
В расчетной схеме взаимодействия сооружения и основания выделяют из этой системы отдельный фундамент шириной b, заменив воздействие на него сооружения соответствующей комбинацией нагрузок. Тогда под действием этих нагрузок, с учетом веса фундамента Q и грунта на его обрезах G по подошве фундамента возникнут реактивные нормальные напряжения р (х), отражающие силы взаимодействия сооружения, фундамента и грунтов основания. Поскольку подошва фундамента всегда заглубляется ниже поверхности земли, в уровне подошвы по сторонам от фундамента будет действовать еще некоторое равномерно распределенное напряжение q, соответствующее весу слоя грунта, равного глубине заложения фундамента d. Тогда можно считать, что на основание в плоскости, проходящей через подошву фундамента, действует нагрузка, составленная из эпюры напряжений р (х) в пределах подошвы фундамента и эпюры равномерно распределенного напряжения q (Рисунок 6, б). Необходимо отметить, что до строительства сооружения в плоскости будущего фундамента уже действуют нормальные напряжения от веса грунта q, поэтому от веса и нагрузок построенного сооружения будут действовать дополнительные напряжения. Они будут равны: р (х) - q. Полные напряжения от всех нагрузок могут быть определены как сумма напряжений от веса грунта, залегающего выше этой точки, и от дополнительной нагрузки под подошвой фундамента р (х) - q. На практике при расчетах фундаментов используют только схему рисунка 6, а.
12 - Определение напряжений по подошве фундаментов и сооружений. При взаимодействии фундаментов и сооружений с грунтами основания на поверхности контакта возникают контактные напряжения. Характер распределения контактных напряжений зависит от жесткости (податливости) грунтов основания. Различают три случая, отражающих способности сооружения и основания к совместной деформации: 1) абсолютно жесткие сооружения, когда деформируемость сооружения ничтожно мала по сравнению с деформируемостью основания, и при определении контактных напряжений сооружение можно рассматривать как недеформируемое (массивные фундаменты под мостовые опоры, тяжелые прессы, дымовые трубы и т.д.); 2) абсолютно гибкие сооружения, когда деформируемость сооружения настолько велика, что оно свободно следует за деформациями основания; 3) сооружения конечной жесткости, когда деформируемость сооружения соизмерима с деформируемостью основания; в этом случае они деформируются совместно, что вызывает перераспределение контактных напряжений. Критерием оценки жесткости сооружения может служить показатель гибкости t по М.И. Горбунову-Посадову:
t ≈ 10 E l3 / Eк h3, (3.1)
где E, Eк - модули деформации грунта основания и материала конструкции; l, h - длина и толщина конструкции.
Конструкция сооружения считается абсолютно жесткой, если t ≤ 1. в первом приближении жесткость конструкции можно оценить исходя из соотношения ее толщины и длины. При h / l > 1 конструкция может рассматриваться как абсолютно жесткая. Существенное значение имеет также соотношение длины l и ширины b сооружения. При l / b ≥ 10 распределение контактных напряжений соответствует случаю плоской задачи, при l / b < 10 - пространственной. При определении контактных напряжений важную роль играет выбор расчетной модели основания и метода решения контактной задачи, причем расчетная модель основания часто бывает не связана собственно с моделью грунтов, слагающих массив, поэтому модели грунтового основания для расчетов контактных напряжений иногда называют контактными моделями. Наибольшее распространение в инженерной практике получили модель местных упругих деформаций и модель упругого полупространства
13 - Определение напряжений в грунтовом массиве от действия местной нагрузки на его поверхности. Распределение напряжений в основании определяется методами теории упругости. Основание при этом рассматривают как упругое полупространство, бесконечно простирающееся во все стороны от горизонтальной поверхности загружения. Напряжение стабилизировано. В основе решения задачи о распределении напряжений в упругом полупространстве под действием местной нагрузки лежит действие вертикальной сосредоточенной силы, приложенной к поверхности упругого полупространства (1885 г., Ж. Буссинеск). Это решение позволяет определить все компоненты напряжений и деформаций в любой точке полупространства М от действия силы Р. Допустим, что положение точки М определяется полярными координатами (Рисунок 9, а) R и β системы координат с началом в точке приложения силы Р. Под действием силы Р точка М переместится в направлении радиуса R на величину S1. Чем дальше от точки О будет расположена точка М, тем меньше будет ее перемещение. При R = ∞ перемещение точки М будет равно 0. Для практических расчетов (в частности, для определения осадки фундамента) наибольшее значение имеют вертикальные напряжения:
σ z = (K / z2 ) . P, где К - коэффициент влияния. Его величина зависит только от отношения r / z, для разных соотношений составлены специальные таблицы. Коэффициент К можно определить по формуле:
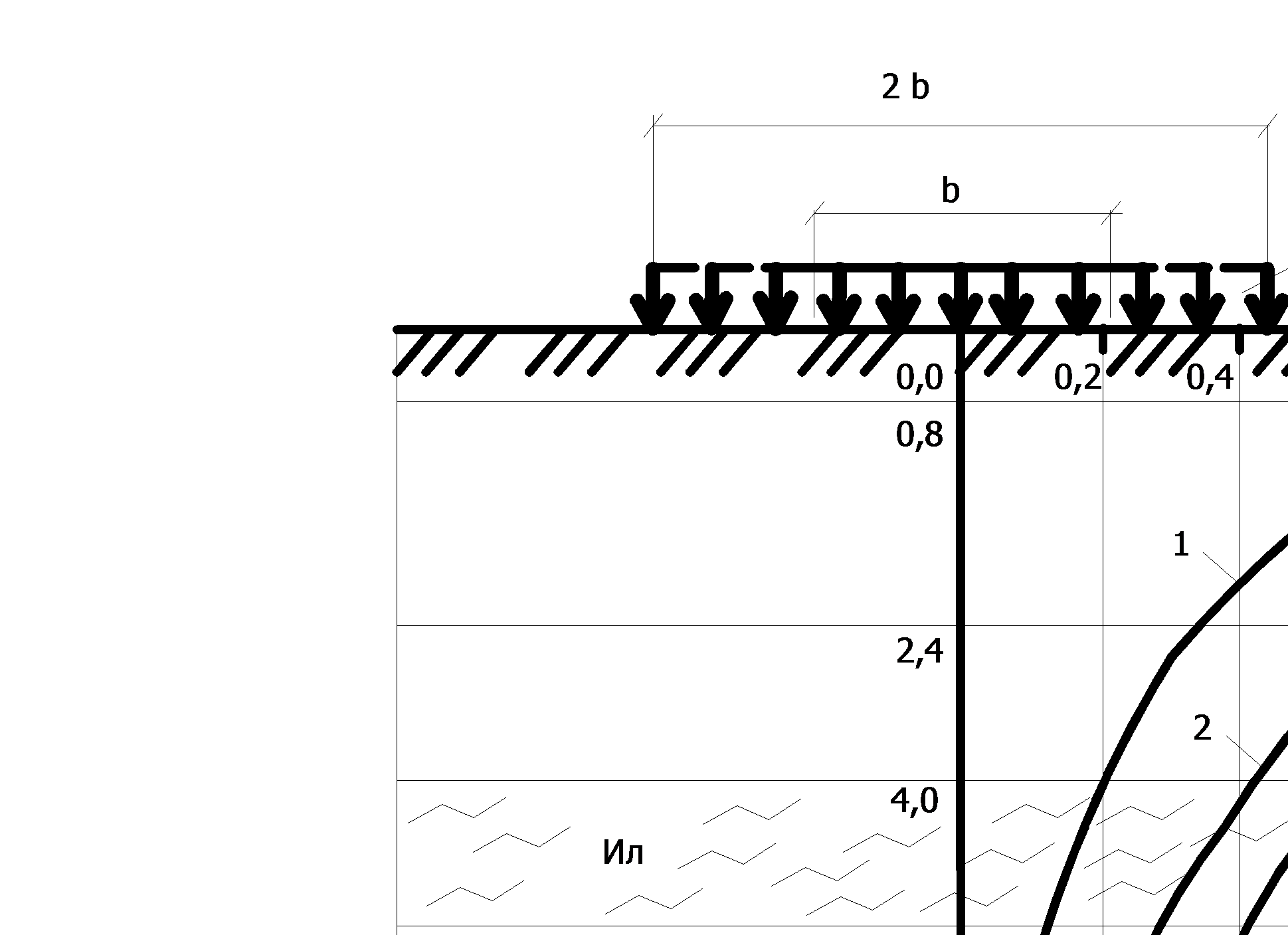
К = (3 / 2π) / (1 / [1 + (r / z)2 ] 5/2, 14 - Влияние формы и площади фундамента в плане. В качестве примера на рисунке 10 в относительных координатах построены такие эпюры для разных случаев.
Рисунок 10 - Характер распределения напряжений σ z по оси фундамента в зависимости от формы и площади его подошвы: 1 – для квадратного фундамента при l = b; 2 – для ленточного фундамента (l ≥ 10 b); 3 - то же, шириной 2b
Увеличение ширины, а следовательно и площади фундамента (кривая 3) приводит к более медленному затуханию напряжений с глубиной. Это обстоятельство объяснимо из принципа суперпозиции. Если ленточный фундамент представить как ряд квадратных фундаментов, установленных вплотную друг к другу, можно с помощью метода угловых точек учесть дополнительное влияние нагрузки, действующей на соседние фундаменты. Указанная закономерность имеет важное практическое значение. Если, например, в основании на некоторой глубине залегает слабый прослоек (ил на рисунке 10), то можно подобрать такую форму и площадь фундамента, чтобы напряжения на кровле этого прослойка были меньше его несущей способности. В противном случае возможны чрезмерные осадки из-за выдавливания грунта слабого прослойка в стороны от оси фундамента.
15 - Определение напряжений в массиве грунтов от действия собственного веса. Напряжения, возникающие в массиве грунтов от действия сооружения, накладываются на поле начальных напряжений, сформировавшихся в массиве к моменту строительства. В общем случае начальные напряжения определяются не только силами гравитации (собственным весом грунта), но и изменением этих сил в процессе формирования массива (увеличение или уменьшение грунтовой толщи), тектоническими, сейсмическими воздействиями и рядом других факторов. Начальное напряженное состояние массива грунта может также изменяться в период работ нулевого цикла: вследствие выемки грунта при разработке котлована, водопонижения, трамбования или укатки грунта и т. п. В этих случаях состояние грунта не начальное, а исходное. Точное определение начального и исходного напряженного состояния очень сложная задача. В инженерной практике используют упрощенное представление: природные напряжения определяют только силами гравитации, т. е. под действием собственного веса. При этом считают, что все деформации массива от собственного веса грунта уже прекратились и напряжения полностью стабилизировались. Тогда при горизонтальной поверхности массива грунтов напряжения на глубине z определяют по выражениям: х σ z = ∫ γ (z)dz; σ х = σ y = ξ σ z; о τ x y = τ y z = τ z x = 0, (4.1)
где γ – удельный вес грунта; ξ - коэффициент бокового давления грунта в состоянии покоя, который может изменяться от 0 до 1 и который определяют по формуле (4.2):
ξ = σ х / σ z = σ y / σ z, (4.2)
Отсюда можно показать, что для однородных напластований при γ (z) = const вертикальные напряжения от собственного веса грунта на глубине z от поверхности определяются формулой (4.3):
σ z = γ z, (4.3)
Эпюра природных напряжений при этом будет иметь вид треугольника При неоднородном напластовании с горизонтальным залеганием слоев эта эпюра будет уже ограничиваться ломаной линией
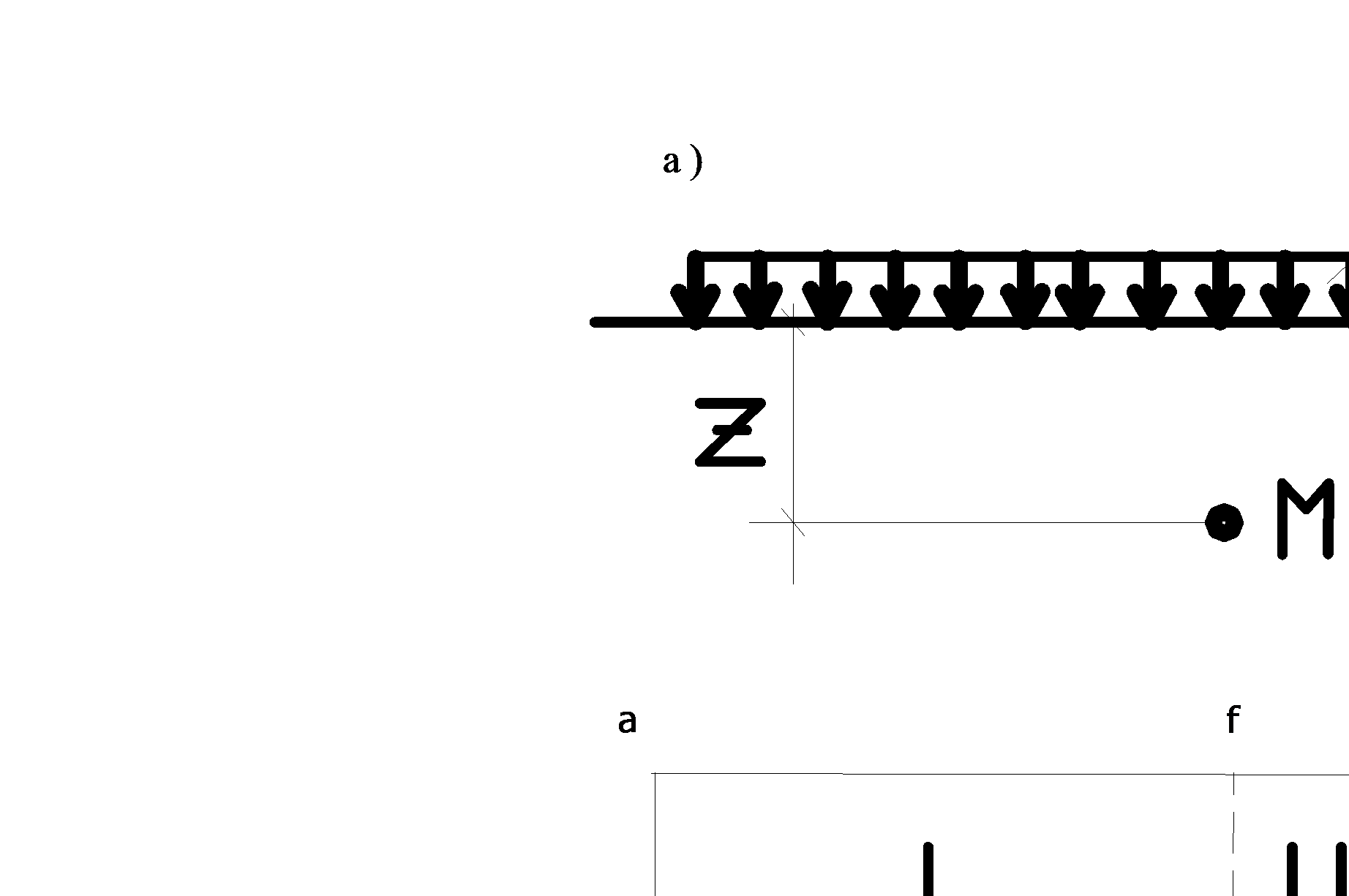
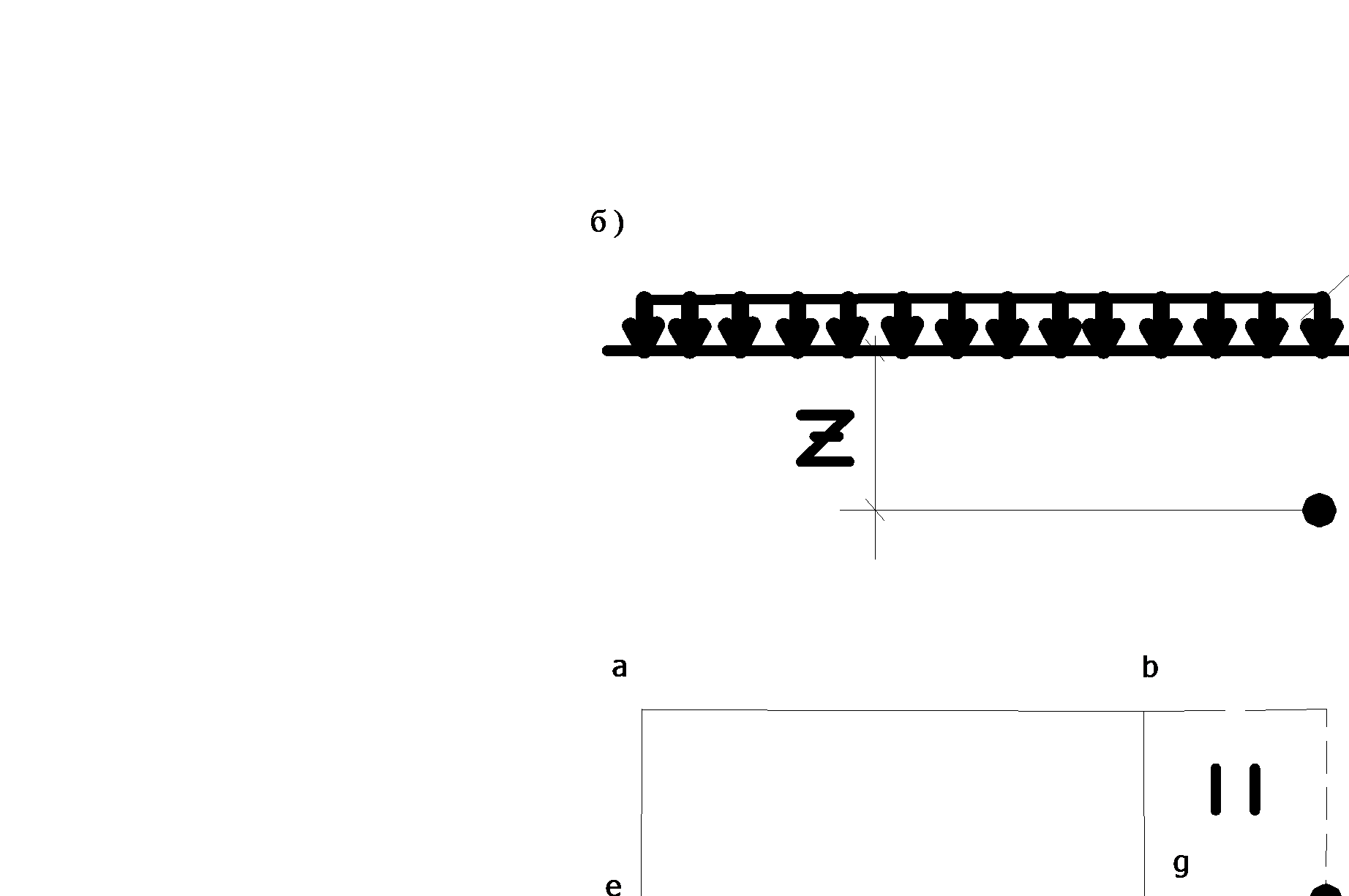
16 - Определение напряжений по методу угловых точек. если проекция рассматриваемой точки М' на горизонтальную поверхность полупространства (точка М) располагается в пределах площади загружения (Рисунок 13, а), то эту площадь можно разбить на четыре прямоугольника (I – Мeaf, II – Mfbg, III – Mgch, IV - Mhde) таким образом, чтобы точка М являлась угловой точкой каждого из них. Тогда напряжение σ z найдем суммированием напряжений под угловыми точками четырех площадей загружения: σ z = σ zI + σ zII + σ z III + σ zIV = 0, 25 (α I + α II + α III + α IV) p, (4.6)
где α I, α II, α III, α IV – коэффициенты, принимаемые по таблице 3.1 в зависимости от отношения сторон площадей загружения I, II, III, IV и отношения z (глубины расположения точки М') к ширине каждой из этих площадей.
Рисунок 13 – Схемы к расчету напряжений в точке М при различном ее расположении
Когда проекция точки М' на горизонтальную поверхность полупространства (точка М) располагается вне пределов площади загружения (Рисунок 13, б), точку М аналогично можно представить как угловую точку фиктивных площадей загружения I, II, III, IV (Мeaf, Mfbg, Mgch, Mhde). При этом в пределах площадей II и IV фиктивная нагрузка прикладывается в обратном направлении. Напряжения определяют из выражения (4.7):
σ z = σ zI - σ zII + σ z III - σ zIV = 0, 25 (α I - α II + α III - α IV) p, (4.7)
В случае расположения точки М' так, как показано на рисунке 13, в, ее проекцию на горизонтальную поверхность полупространства (точку М) можно представить как угловую точку фиктивных площадей загружения Мhae (I), Mgbe (II), Mhdf (III), Mgcf (IV), и тогда:
σ z = 0, 25 (α I - α II - α III + α IV) p, (4.8)
Таким образом, пользуясь методом угловых точек, можно найти напряжение σ z в любой точке полупространства, к поверхности которого приложена равномерно распределенная нагрузка в пределах прямоугольной площади.
17 - Действие равномерно распределенной полосовой нагрузки (плоская задача). По мере увеличения отношения длины площади загружения l к ее ширине задача по определению напряжений все с большим основанием может рассматриваться как плоская (плоская деформация). При бесконечной длине полосы нагрузки l в каждом сечении, перпендикулярном ее продольной оси, будет одинаковая картина напряжений. Обычно рассматривают плоскую задачу, когда l: b ≥ 10. В таком случае определяют три составляющих: нормальные напряжения σ z, σ у и касательные напряжения τ yz. Указанные выше сечения остаются в процессе деформации плоскими (плоская деформация), и, следовательно, τ ху = τ хz = 0, а является функцией σ z и σ у . Если во всех точках перпендикулярного продольной оси нагрузки сечения изотропного тела определить σ z, σ у и τ yz соединить точки с одинаковыми значениями каждой из этих величин линиями равных напряжений, то получим своеобразные графики (Рисунок 14). Эти графики показывают, что нормальные напряжения σ z распространяются на значительную глубину (цифры на линиях указывают долю от нагрузки р), а нормальные напряжения σ у и касательные напряжения τ уz – в пределах полутора-двух ширин полосы загружения. По этим графикам, применяя интерполяцию, можно найти значения σ z, σ у и τ yz в любой точке.
18 - Прочность, устойчивость грунтовых массивов и давление грунтов на ограждения. Основные положения теории предельного равновесия. Практика показывает, что при определенных условиях может произойти потеря устойчивости части грунтового массива, которая сопровождается разрушением построенного на нем сооружения. К таким условиям можно отнести: недостаточную площадь фундаментов, чрезмерную крутизну откосов, неудачно запроектированную подпорную стенку и т.п. Это связано с формированием в массиве грунтов областей, где соотношение между действующими напряжениями становится таким, что прочность грунта оказывается исчерпанной. Для элементарного объема грунта могут существовать такие соотношения напряжений, при которых грунт находится в состоянии предельного равновесия, в этом случае рассмотренные ранее зависимости выражают условие предельного равновесия в точке грунтового массива. В реальных условиях, когда грунтовый массив является основанием или средой, в которой строят сооружение, в нем формируется неоднородное поле напряжений. В этом случае в каждой точке грунтового массива действующие напряжения будут различными. Если распределение напряжений в массиве определено и заданы прочностные характеристики грунтов, то оказывается возможным произвести оценку напряженного состояния в любой точке массива. Задачи этого типа решаются с помощью теории предельного напряженного состояния (теории предельного равновесия), начальные сведения о которой были рассмотрены в предыдущих лекциях. Необходимо отметить, что теория предельного равновесия исследует только напряженное состояние массива грунт
|


 в горизонтальном направлении, когда теннисист произвел по мячу резкий удар длительностью
в горизонтальном направлении, когда теннисист произвел по мячу резкий удар длительностью 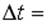 0, 1 с. Изменившийся импульс мяча стал равным
0, 1 с. Изменившийся импульс мяча стал равным  (масштаб указан на рисунке).
(масштаб указан на рисунке). 

 ] b) [
] b) [  ] c) [
] c) [  ]
] изменился под действием кратковременного удара и стал равным
изменился под действием кратковременного удара и стал равным  , как показано на рисунке.
, как показано на рисунке. 

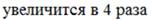 b) [ ]
b) [ ] 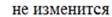
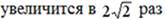 d) [ ]
d) [ ] 

 ] b) [
] b) [  ] c) [
] c) [  ]
] 2.
2. ]
] ]
] ]
] ] e) [
] e) [ 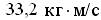 ]
]
 b)
b)  c)
c)  d)
d) 

 ] b) [
] b) [  ] c) [
] c) [  ]
]
 b)
b)  c)
c)  d)
d) 

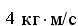 ]
] ]
]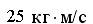 ]
] ]
] ]
]
 b)
b)  c)
c)  d)
d) 

 2.
2.
 b)
b)  c)
c)  d)
d)  e)
e) 

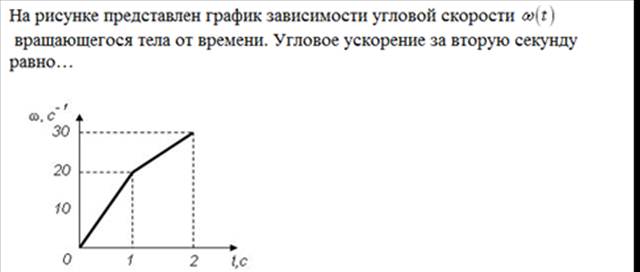 a) [
a) [  ] b) [
] b) [ 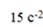 ] c) [
] c) [  ] d) [
] d) [  ] e) [
] e) [  ]
] . Под действием трения стержень остановился, при этом выделилось тепло Q1.
. Под действием трения стержень остановился, при этом выделилось тепло Q1. 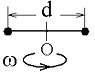 Если стержень раскручен до угловой скорости
Если стержень раскручен до угловой скорости 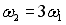 , то при остановке стержня выделится тепло …
, то при остановке стержня выделится тепло … b)
b)  c)
c) 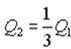 d)
d) 


 b)
b)  c)
c)  d)
d) 
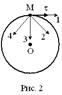
 . На рис.1 показан график зависимости проекции скорости
. На рис.1 показан график зависимости проекции скорости  от времени (
от времени ( – единичный вектор положительного направления,
– единичный вектор положительного направления,  – проекция
– проекция  на это направление). При этом вектор полного ускорения на рис.2 имеет направление …
на это направление). При этом вектор полного ускорения на рис.2 имеет направление …

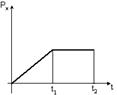
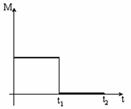 Диск вращается равномерно с некоторой угловой скоростью
Диск вращается равномерно с некоторой угловой скоростью  . Начиная с момента времени t=0, на него действует момент сил, график временной зависимости которого представлен на рисунке.
. Начиная с момента времени t=0, на него действует момент сил, график временной зависимости которого представлен на рисунке. b) [
b) [ 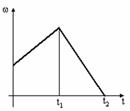 c)
c) 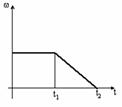 d)
d) 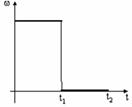 ]
] от времени (
от времени ( – единичный вектор положительного направления,
– единичный вектор положительного направления,  – проекция
– проекция  на это направление). На рис.2 укажите направление силы, действующей на т.М в момент времени t1.
на это направление). На рис.2 укажите направление силы, действующей на т.М в момент времени t1.


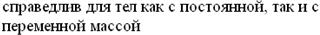
 .
.  Скорость шайбы в точке С …
Скорость шайбы в точке С …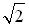 раз больше, чем в точке В b) в 4 раза больше, чем в точке В
раз больше, чем в точке В b) в 4 раза больше, чем в точке В раза больше, чем в точке В d) в 2 раза больше, чем в точке В
раза больше, чем в точке В d) в 2 раза больше, чем в точке В

 b)
b) 
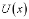 . При движении тела сила трения совершила работу
. При движении тела сила трения совершила работу  = 20 Дж.
= 20 Дж. После абсолютно неупругого удара тела со стеной в точке В выделилось...
После абсолютно неупругого удара тела со стеной в точке В выделилось...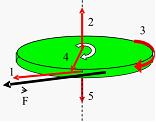 a) 1
a) 1
 b)
b) 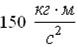 c)
c)  d)
d) 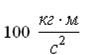
 пропорциональна градиенту потенциальной энергии
пропорциональна градиенту потенциальной энергии  . Если график зависимости потенциальной энергии
. Если график зависимости потенциальной энергии  от координаты x имеет вид, представленный на рисунке,
от координаты x имеет вид, представленный на рисунке, 
 на ось X будет….
на ось X будет…. b)
b) 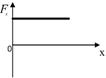 c)
c)  d)
d) 


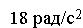 ] b) [
] b) [  ] c) [
] c) [  ] d) [
] d) [ 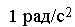 ]
] – сила тяжести;
– сила тяжести;  – сила Архимеда и
– сила Архимеда и  – сила сопротивления, то при равномерном движении шарика…
– сила сопротивления, то при равномерном движении шарика… b)
b) 
 d)
d) 


 ] b) [
] b) [  ] c) [
] c) [  ] d) [
] d) [  ]
]
 b)
b) 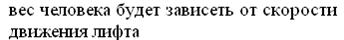
 d)
d)