Тангенциальное, нормальное и полное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рисунок 1 – Тангенциальное ускорение Направление вектора тангенциального ускорения Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения, показано на рис. 1. Нормальное ускорение характеризует изменение скорости по направлению и обозначается Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
или
Направление полного ускорения также определяется правилом сложения векторов:
1.1.5 Поступательное и вращательное движение абсолютно твёрдого тела Движение тела считается поступательным, если любой отрезок прямой линии, жестко связанный с телом, всё время перемещается параллельно самому себе. При поступательном движении все точки тела совершают одинаковые перемещения, проходят одинаковые пути, имеют равные скорости и ускорения, описывают одинаковые траектории. Вращение твёрдого тела вокруг неподвижной оси – движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, перпендикулярной плоскостям этих окружностей. Сама эта прямая является осью вращения. При вращении тела радиус окружности, описываемой точкой этого тела, повернётся за интервал времени на некоторый угол. Вследствие неизменности взаимного расположения точек тела на такой же угол повернуться за тоже время радиусы окружностей, описываемых любыми другими точками тела. Этот угол является величиной, характеризующей вращательное движение всего тела в целом. Отсюда можно сделать вывод, что для описания вращательного движения абсолютно твёрдого тела вокруг неподвижной оси надо знать только одну переменную – угол, на который повернётся тело за определённое время. Связь между линейной и угловой скоростями для каждой точки твёрдого тела даётся формулой:
Также точки твёрдого тела имеют нормальные и тангенциальные ускорения, которые можно задать формулами:
Плоскопараллельное движение – движение, при котором каждая точка тела движется постоянно в одной плоскости, при этом все плоскости параллельны между собой. [3, с. 375]
|

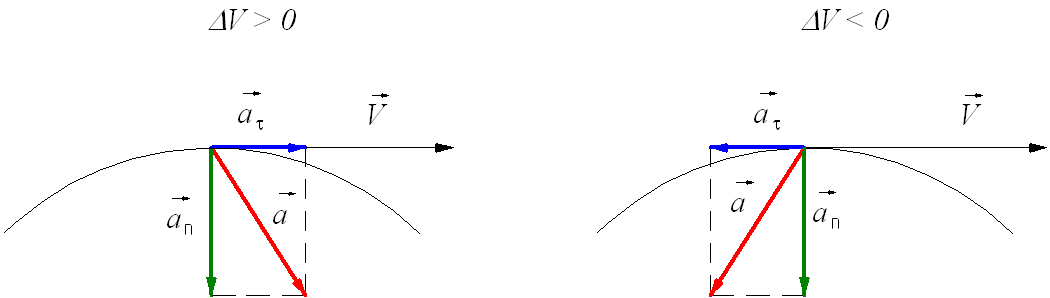
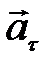 совпадает с направлением линейной скорости или противоположно ему, из рис. 1. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
совпадает с направлением линейной скорости или противоположно ему, из рис. 1. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.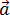 n. Вектор нормального ускорения направлен по радиусу кривизны траектории.
n. Вектор нормального ускорения направлен по радиусу кривизны траектории. (9)
(9) (10)
(10)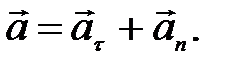 (11)
(11)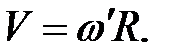 (12)
(12)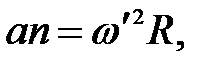
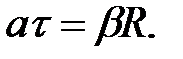 (13)
(13)


