Линейная алгебра
Варианты контрольных заданий для студентов 1-го курса дневного отделения
Хабаровск 2008 ББК Х 12 Математика. Линейная алгебра: варианты контрольных заданий для студентов 1-го курса дневного отделения / сост. Е. О. Старкова, М. Ф. Тиунчик, С. В. Тонконог. – Хабаровск: РИЦ ХГАЭП, 2008. – 32 с.
Рецензент канд. физ.-мат. наук, доцент, начальник отделения подготовки научно-педагогических кадров ХПИ ФСБ России Ивлева А.И.
Утверждено издательско-библиотечным советом академии в качестве методических указаний
Тиунчик Михаил Филиппович Старкова Елена Олеговна Тонконог Светлана Владимировна МАТЕМАТИКА
Линейная алгебра Варианты контрольных заданий для студентов 1-го курса дневного отделения
Редактор Г.С. Одинцова
680042, Хабаровск, ул.Тихоокеанская, 134, ХГАЭП, РИЦ
© Хабаровская государственная академия экономики и права, 2008
Предисловие
В методической разработке приведены 30 вариантов контрольных упражнений по линейной алгебре. Каждый вариант состоит из 15 типовых заданий. В вариантах предусмотрены задания на темы: действия над матрицами, вычисление определителей, методы исследования и решения систем линейных алгебраических уравнений, приведение систем к системе с базисом и нахождение базисных решений, нахождение опорных решений канонических систем уравнений методом однократного замещения, нахождение собственных векторов и собственных значений линейных преобразований, исследование квадратичных форм. Материал соответствует государственным образовательным стандартам по математическим дисциплинам для студентов экономических специальностей. Для студентов специальностей «Экономическая теория» и «Математически методы в экономике», изучающих линейную алгебру отдельной дисциплиной, вариант выдаётся в полном объёме как индивидуальное задание на семестр. По темам аналитической геометрии, изучение которых отнесено к этой дисциплине, выполняется отдельное индивидуальное задание или аудиторная контрольная работа. Для остальных специальностей вариант выдаётся не в полном объёме, а только по материалу, изучение которого предусмотрено соответствующим стандартом.
Линейная алгебра Контрольное задание для студентов 1-го Курса
1. Для данных матриц А и В и заданных чисел α, β требуется найти: 1) АВ; 2) α А · В; 3) β А – Е, где Е – единичная матрица; 4) транспонированные матрицы АТ и ВТ.
2. По данной матрице вычислить её определитель следующими способами: 1) разложением по элементам какой-нибудь строки; 2) разложением по элементам какого-либо столбца; 3) методом Гаусса.
3. По заданной матрице А найти её обратную А-1 и проверить равенства А · А-1 = А-1 · А = Е.
4. При заданных матрицах А и В найти неизвестную матрицу Х, удовлетворяющую матричному уравнению АХ = В. 5. Найти общее решение данной однородной системы линейных алгебраических уравнений с помощью её фундаментальной системы решений. 6. При заданных А и В найти общее решение неоднородной системы АХ = В, используя фундаментальную систему решений соответствующей приведённой однородной системы уравнений. 7. Найти общее решение данной системы линейных алгебраических уравнений методом Гаусса. 8. Вычислить ранг заданной матрицы. 9. Заданную систему линейных уравнений исследовать на совместность по критерию совместности (по теореме Кронекера – Капелли) и на определённость. 10. Решить систему линейных алгебраических уравнений следующими способами: 1) по формулам Крамера; 2) матричным методом; 3) методом Гаусса. 11. Данную систему линейных уравнений привести к системе с базисом методом Жордана – Гаусса и найти одно базисное решение. 12. Найти три опорных решения данной канонической системы линейных уравнений методом преобразования однократного замещения. 13. Найти собственные векторы и собственные значения линейного преобразования переменных, заданного матрицей А. 14. Привести данную квадратичную форму к каноническому виду методом ортогональных преобразований. Выяснить, является ли она положительно определённой. 15. Выяснить с помощью критерия Сильвестра, является ли квадратичная форма положительно определённой.
Вариант 1
1. 2. 4.
6. 7.
8. 10. 12.
14.
Вариант 2
1.
2. 4. 6. 8. 10. 12. 14. Вариант 3
1.
2. 4. 6. 8. 10. 12.
14. Вариант 4
1. 2. 4. 6. 8. 10. 12. 14. Вариант 5
1.
2. 4. 6. 8. 10. 12. 14. Вариант 6 1.
2. 4. 6. 8. 10. 12. 14. Вариант 7 1.
2. 4. 6. 8. 10. 12. 14. Вариант 8 1.
2. 4. 6. 8. 10. 12. 14. Вариант 9 1.
2. 4. 6. 8. 10. 12. 14. Вариант 10 1.
2. 4. 6. 8. 10. 12. 14. Вариант 11 1.
2. 4. 6. 8. 10. 12. 14. Вариант 12 1.
2. 4. 6. 8. 10. 12. 14. Вариант 13 1.
2. 4. 6. 8. 10. 12. 14. Вариант 14 1.
2. 4. 6. 8. 10. 12. 14.
Вариант 15 1.
2. 4. 6. 8. 10. 12. 14. Вариант 16 1.
2. 4. 6. 8. 10. 12. 14. Вариант 17 1. 2. 4. 6. 8. 10. 12. 14. 15. Вариант 18 1. 2. 4. 6. 8. 10. 12. 14. 15. Вариант 19 1.
2. 4. 6. 8. 10. 12. 14. 15. Вариант 20 1.
2. 4. 6. 8. 10. 12. 14. Вариант 21 1.
2. 4. 6. 8. 10. 12. 14. Вариант 22 1.
2. 4. 6. 8. 10. 12. 14. Вариант 23 1.
2. 4. 6. 8. 10. 12. 14. Вариант 24 1. 2. 4. 6. 8. 10. 12. 14. 15. Вариант 25 1.
2. 4. 6. 8. 10. 12. 14. Вариант 26 1.
2. 4. 6. 8. 10. 12. 14. Вариант 27 1. 2. 4. 6. 8. 10. 12. 14. Вариант 28 1. 2. 4. 6. 8. 10. 12. 14. Вариант 29 1.
2. 4. 6. 8. 10. 12. 14. Вариант 30 1.
2. 4. 6. 8. 10. 12. 14.
|

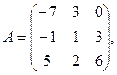
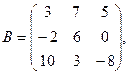 α = 6, β = 3.
α = 6, β = 3.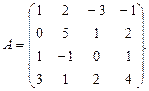 3.
3. 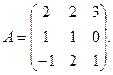
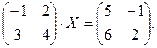 5.
5. 
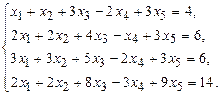
 9.
9. 
 11.
11. 
 13.
13. 
 15.
15. 

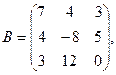 α = 2, β = 4.
α = 2, β = 4. 3.
3. 
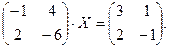 5.
5. 

 7.
7. 
 9.
9. 
 11.
11. 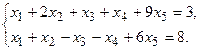
 13.
13. 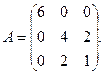
 15.
15. 
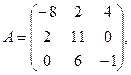
 α = – 2, β = 5.
α = – 2, β = 5. 3.
3. 
 5.
5. 

 7.
7. 
 9.
9. 
 11.
11. 
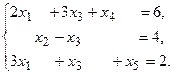 13.
13. 
 15.
15. 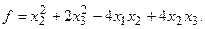
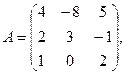
 α = 4, β =
α = 4, β = 
 3.
3. 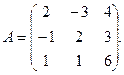
 5.
5. 
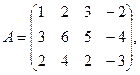
 7.
7. 
 9.
9. 
 11.
11. 
 13.
13. 
 15.
15. 

 α = 3, β = 5.
α = 3, β = 5. 3.
3. 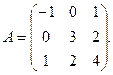
 5.
5. 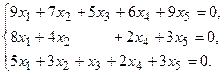
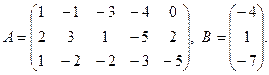 7.
7. 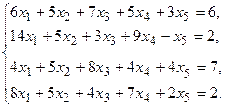
 9.
9. 
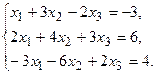 11.
11. 
 13.
13. 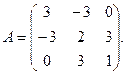
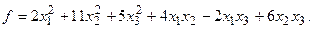 15.
15. 

 α = – 2, β = 3.
α = – 2, β = 3. 3.
3. 
 5.
5. 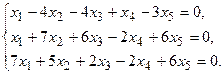
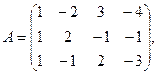
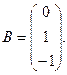 7.
7. 
 9.
9. 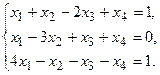
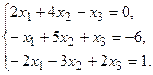 11.
11. 
 13.
13. 
 15.
15. 

 α = – 5, β = 3.
α = – 5, β = 3. 3.
3. 
 5.
5. 

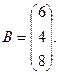 7.
7. 
 9.
9. 
 11.
11. 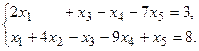
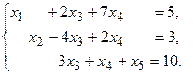 13.
13. 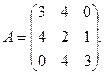
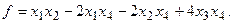 15.
15. 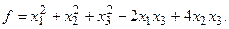

 α = 10, β = – 3.
α = 10, β = – 3. 3.
3. 
 5.
5. 
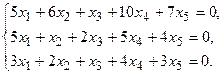

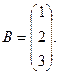 7.
7. 
 9.
9. 
 11.
11. 
 13.
13. 
 15.
15. 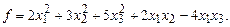

 α = – 3, β = 10.
α = – 3, β = 10. 3.
3. 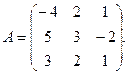
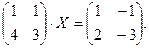 5.
5. 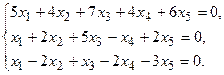
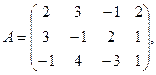
 7.
7. 
 9.
9. 
 11.
11. 
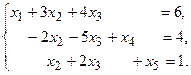 13.
13. 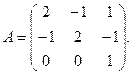
 15.
15. 

 α = – 6, β = 4.
α = – 6, β = 4.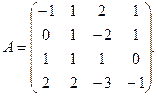 3.
3. 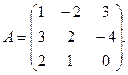
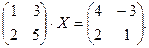 5.
5. 

 7.
7. 
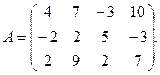 9.
9. 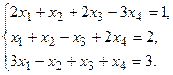
 11.
11. 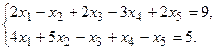
 13.
13. 
 15.
15. 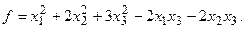

 α = – 2, β = 3.
α = – 2, β = 3. 3.
3. 
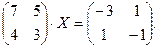 5.
5. 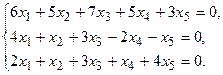

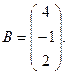 7.
7. 
 9.
9. 
 11.
11. 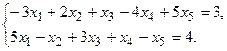
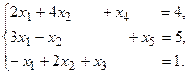 13.
13. 
 15.
15. 

 α = 9, β = – 3.
α = 9, β = – 3.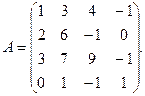 3.
3. 
 5.
5. 

 7.
7. 
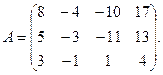 9.
9. 
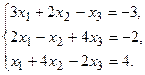 11.
11. 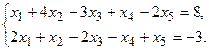
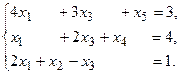 13.
13. 
 15.
15. 

 α = – 10, β = – 2.
α = – 10, β = – 2. 3.
3. 
 5.
5. 
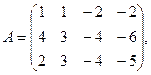
 7.
7. 
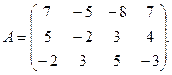 9.
9. 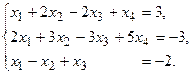
 11.
11. 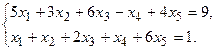
 13.
13. 
 15.
15. 

 α = – 2, β = 4.
α = – 2, β = 4.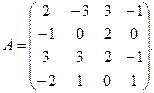 3.
3. 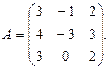
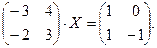 5.
5. 

 7.
7. 
 9.
9. 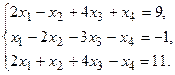
 11.
11. 
 13.
13. 
 15.
15. 

 α = – 9, β = 5.
α = – 9, β = 5. 3.
3. 
 5.
5. 
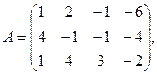
 7.
7. 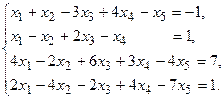
 9.
9. 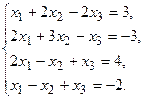
 11.
11. 
 13.
13. 
 15.
15. 

 α =
α =  , β = 10.
, β = 10.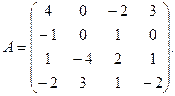 3.
3. 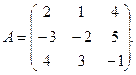
 5.
5. 

 7.
7. 
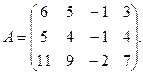 9.
9. 
 11.
11. 
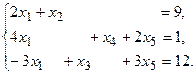 13.
13. 
 15.
15. 

 α = – 4, β = 5.
α = – 4, β = 5. 3.
3. 
 5.
5. 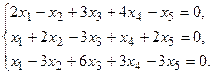
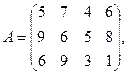
 7.
7. 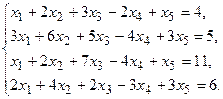
 9.
9. 
 11.
11. 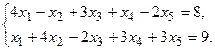
 13.
13. 
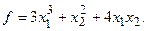
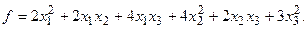
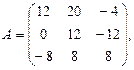
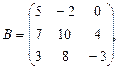 α =
α =  , β = 4.
, β = 4. 3.
3. 
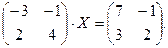 5.
5. 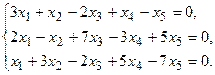

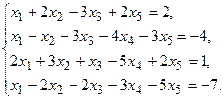
 9.
9. 
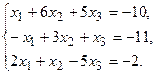 11.
11. 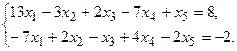
 13.
13. 



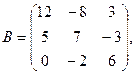 α = 11, β = 7.
α = 11, β = 7. 3.
3. 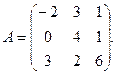
 5.
5. 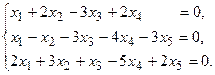
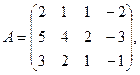
 7.
7. 
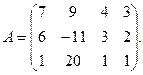 9.
9. 
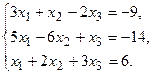 11.
11. 
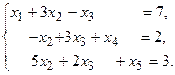 13.
13. 

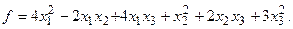

 α = 3, β = – 5.
α = 3, β = – 5. 3.
3. 
 5.
5. 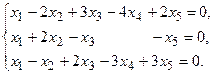
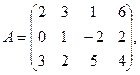
 7.
7. 
 9.
9. 
 11.
11. 
 13.
13. 


 α = 3, β = – 2.
α = 3, β = – 2.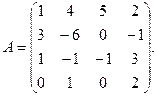 3.
3. 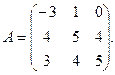
 5.
5. 
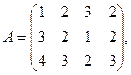
 7.
7. 
 9.
9. 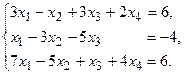
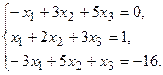 11.
11. 
 13.
13. 
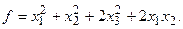 15.
15. 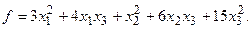

 α = 5, β = –3.
α = 5, β = –3. 3.
3. 
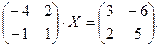 5.
5. 

 7.
7. 
 9.
9. 
 11.
11. 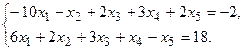
 13.
13. 
 15.
15. 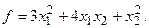
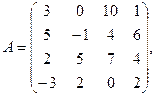
 α = 4, β = – 5.
α = 4, β = – 5. 3.
3. 
 5.
5. 
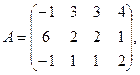

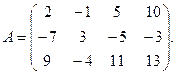 9.
9. 
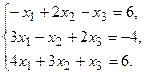 11.
11. 
 13.
13. 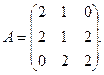
 15.
15. 
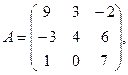
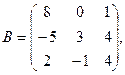 α = – 7, β = 2.
α = – 7, β = 2. 3.
3. 
 5.
5. 

 7.
7. 
 9.
9. 
 11.
11. 
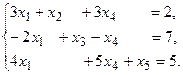 13.
13. 
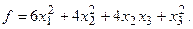

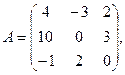
 α = 6, β = – 4.
α = 6, β = – 4. 3.
3. 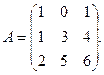
 5.
5. 

 7.
7. 
 9.
9. 
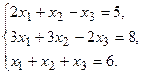 11.
11. 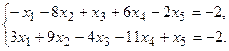
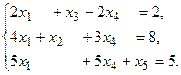 13.
13. 
 15.
15. 

 α = 8, β = – 3.
α = 8, β = – 3.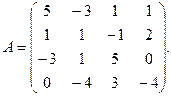 3.
3. 
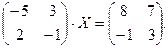 5.
5. 

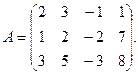 9.
9. 
 11.
11. 
 13.
13. 
 15.
15. 
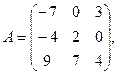
 α = – 5, β = 2.
α = – 5, β = 2.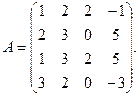 3.
3. 
 5.
5. 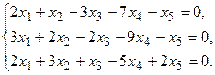
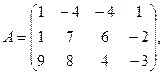
 7.
7. 
 9.
9. 
 11.
11. 
 13.
13. 
 15.
15. 

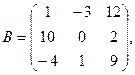 α = 6, β = –2.
α = 6, β = –2. 3.
3. 
 5.
5. 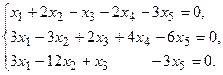

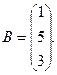 7.
7. 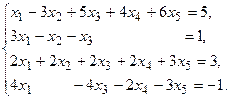
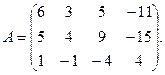 9.
9. 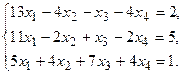
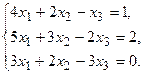 11.
11. 
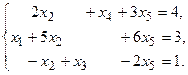 13.
13. 
 15.
15. 

 α = 3, β = 4.
α = 3, β = 4. 3.
3. 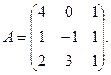
 5.
5. 

 7.
7. 
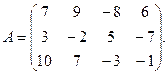 9.
9. 
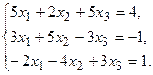 11.
11. 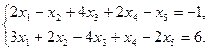
 13.
13. 
 15.
15. 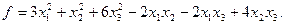

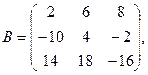 α = 5, β =1/2.
α = 5, β =1/2. 3.
3. 
 5.
5. 

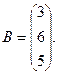 7.
7. 
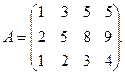 9.
9. 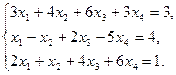
 11.
11. 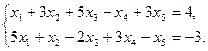
 13.
13. 
 15.
15. 



