Типы возрастной структуры населения
3. Формулы по теме «Сводка и группировка данных»
4. Формулы по теме «Абсолютные и относительные величины»
Продолжение приложения 4
5. Формулы по теме «Средние величины» а) виды средних
Продолжение приложения 5
б) структурные средние
Продолжение приложения 5
6. Формулы по теме «Показатели вариации, дисперсионный анализ»
Продолжение приложения 6
7. Формулы по теме «Выборочное наблюдение»
Продолжение приложения 7
8. Формулы по теме «Статистическое изучение динамики»
Продолжение приложения 8
Продолжение приложения 8
9. Формулы по теме «Индексы. Анализ индексным методом»
10. Формулы по теме «Статистические методы изучения взаимосвязей»
Продолжение приложения 10
Список рекомендуемой литературы: 1. Гинзбург А.И. Статистика: СПб: Питер, 2003. - 128 с. 2. Гусаров В.М. Статистика: учебное пособие для вузов /В.М. Гусаров. - М.: ЮНИТИ, 2003. - 463 с. 3. Зинченко А.П. Сельскохозяйственная статистика с основами социально-экономической статистики: учебник /А.П. Зинченко, МСХА. - М.: МСХА, 1998. - 430 с. 4. Зинченко А.П. Сельскохозяйственные предприятия: экономико-статистический анализ: учебное пособие /А.П. Зинченко. - М.: Финансы и статистика, 2002. - 160 с. 5. Петрова Е.В. Практикум по статистике транспорта: учебное пособие /Е.В. Петрова, О.И. Ганченко, И.М. Алексеева. - М.: Финансы и статистика, 2002. – 368 с. 6. Салина В.Н. Статистика финансов: учебное пособие для вузов. - М.: ГрифМО РФ. 2-е издание: М, Финансы и статистика, 2002. - 810 с. 7. Статистика: учебн. пособие/ А.В. Багат [и др.]; ред. В.М.Симчера.-М.: Финансы и статистика, 2008. – 368 с. 8. Салина В.Н. Статистика финансов: учебное пособие для вузов. - М.: ГрифМО РФ. 2-е издание.: М, Финансы и статистика, 2002. - 810 с. 9. Статистика: учеб. /В.Г. Минашкин и [др].; ред. В.Г. Минашкин. - М.: Проспект, 2006. - 272 с. 10.Статистика: учебник/ред. И.И. Елисеева. - М.: Высшее образование, 2009. – 566 с. 11.Статистика: учебник /ред. И.И. Елисеева. - СПб.: Питер, 2010. – 368 с. 12.Статистика и бухгалтерский учет: учебное пособие /А.П. Зинченко [и др.]. - М.: КолосС, 2008. – 438 с. 13.Рудакова Р.П, Букин Л.Л. Практикум по статистике. - СПб.: Питер, 2007. - 288 с.: ил.-(Серия учебное пособие). 14.Рудакова Р.П., Букин Л.Л., Гаврилов В.И. Статистика: учебное пособие, - СПб.: Питер, 2007. 15.Харченко Н.М. Статистика: учебник. - М,: Издательско-торговая корпорация «Дашков и К0», 2007. - 368 с.
Учебное издание
Моисеева Елена Вячеславовна Захарова Анастасия Леонидовна Михайлова Екатерина Львовна Леонтьева Татьяна Геннадьевна Практикум по статистике Часть 1
Подписано в печать 2013 г. Формат 60х84/16. Бумага газетная. Усл. печ. л. 16, 88 Тираж 100 экз. Заказ №
Полиграфический отдел ФГОУ ВПО «Чувашская государственная сельскохозяйственная академия» 428003, г. Чебоксары, ул. К. Маркса, 29
Типы возрастной структуры населения (в %)
Половой состав населения определяется абсолютной численностью мужчин и женщин и их соотношением в общей численности населения. Так же определяется коэффициент соотношения полов (число мужчин на сто или тысячу женщин) по формуле:
Этот коэффициент используется для расчета половых пропорций среди новорожденных. В России в среднем рождается 115 мальчиков на 100 девочек. Из-за более высокой смертности мальчиков к двадцати годам пропорция выравнивается. В России количество женщин преобладает из-за более высокой смертности мужчин во всех возрастных группах и их меньшей продолжительности жизни, чем у женщин. Различают естественное и механическое движение населения. Естественное движение охватывает рождаемость, смертность, заключение и расторжение браков. Показатели воспроизводства населения могут быть выражены в абсолютных величинах: количеством родившихся, умерших, приростом населения за определенный период времени и в относительных величинах в виде коэффициентов. В статистике такие относительные показатели воспроизводства принято исчислять в промилле (%о), то есть на 1000 человек. Коэффициент рождаемости вычисляется путем деления числа родившихся за год N на среднегодовую численность населения
Коэффициент смертности рассчитывается путем деления числа умерших за год М на среднегодовую численность населения
Коэффициент брачности определяется как отношение числа заключенных за год браков к среднегодовой численности населения, а коэффициент разводов - как отношение числа расторгнутых за год браков к среднегодовой численности населения. Для характеристики соотношения между рождаемостью и смертностью исчисляется показатель жизненности:
Чтобы исключить влияние половозрастной структуры, применяют специальный коэффициент рождаемости (коэффициент плодовитости), который рассчитывается как отношение числа родившихся к средней численности женщин в возрасте от 15 до 49 лет
Между общим и специальным коэффициентами рождаемости существует взаимосвязь:
где При изучении смертности определяются коэффициенты детской смертности по формулам:
где m1 - число умерших в текущем году детей в возрасте до 1 года; N1 - число родившихся в текущем году; No - число родившихся в предыдущем году. Коэффициент естественного прироста можно рассчитать по формуле:
или как разность между коэффициентами рождаемости и смертности:
Для характеристики естественного прироста исчисляются: - коэффициент оборота населения:
- коэффициент экономичности воспроизводства населения:
Под механическим движением (миграцией) населения понимают прибытие в данный населенный пункт и выбытие. Рассчитывают абсолютное число прибывшего (П) и выбывшего (В) населения. Поскольку показатели объема миграции зависят от численности населения соответствующей территории, для анализа миграционных процессов используются относительные показатели. Рассмотрим некоторые из них: - коэффициент прибытия
-коэффициент выбытия
-коэффициент миграции (механического прироста)
-коэффициент интенсивности миграционного оборота
- коэффициент эффективности миграции
Прибавив к коэффициенту естественного прироста коэффициент миграции, получим коэффициент общего прироста населения Ко6щ = KN_M + КП-В или Ко6щ = Пример 3. Имеются следующие данные по району, тыс. чел.: 1. Численность населения на начало года 82 в том числе: женщины в возрасте от 15 до 49 лет 23, 5 2. Численность населения на конец года 86 в том числе: женщины в возрасте от 15 до 49 лет 24, 5 3. В течение года: родилось 1, 18 умерло всего 0, 42 из них детей до 1 года 0, 03 Определите: 1. Коэффициенты рождаемости, смертности, естественного прироста. 2. Специальный коэффициент рождаемости. 3. Коэффициент детской смертности. 4. Коэффициент жизненности. Решение: 1. Определим среднегодовую численность населения и женщин в возрасте от 15 до 49 лет:
Рассчитаем коэффициенты рождаемости, смертности, естественного прироста:
На каждую тысячу человек в течение года родилось 14 детей, умерло 5 человек, естественный прирост составил 9 человек. 2. Специальный коэффициент рождаемости равен:
На каждую тысячу женщин в возрасте от 15 до 49 лет в течение года родилось 49 детей. 3. Определим коэффициент детской смертности по формуле:
На тысячу родившихся в данном году умерло 25 детей в возрасте до 1 года. 4. Коэффициент жизненности равен:
Пример 4. Имеются следующие данные по одному из регионов (тыс. чел.): 1. Численность населения на начало года 126 2. В течение года: - родилось 1, 89 - умерло 1, 26 - заключено браков 2, 52 - зарегистрировано разводов 3, 78 - прибыло 0, 63 - убыло 0, 50 Определите за год: 1. Среднюю численность населения. 2. Коэффициенты рождаемости, смертности, естественного прироста, миграции, общего прироста населения, брачности, разводимости. 3. Коэффициент плодовитости (специальный коэффициент рождаемости), если известно, что среднее число женщин в возрасте от 15 до 49 лет составило 32 тыс. чел. Решение: 1. Для расчета средней численности необходимо знать численность населения на конец года: SK=SH+N-M + П-B, где Sh и Sk - численность населения на начало и конец года. SK =126+ 1, 89-1, 26+ 0, 63-0, 50 = 126, 76 тыс. чел. Для расчета средней численности населения воспользуемся формулой средней арифметической простой:
2. Коэффициент естественного прироста определим двумя способами:
Коэффициент миграции равен:
Коэффициент общего прироста определим двумя способами:
3. Коэффициент плодовитости определяем по формуле:
Пример 5. Численность постоянного населения региона на начало года составила 820 тыс. чел., на конец года - 840 тыс. чел., за год в регионе родилось у постоянного населения 16, 6 тыс. чел., умерло 6, 64 тыс. чел. Определите: 1. Коэффициенты рождаемости, смертности, оборота и экономичности воспроизводства населения. 2. Коэффициент жизненности населения. 3. Коэффициент миграции. Покажите роль естественного прироста и миграции в формировании численности населения региона. Решение: 1.Для расчета коэффициентов естественного движения населения определим среднегодовую численность по формуле средней арифметической простой:
Коэффициент оборота населения рассчитаем по формуле:
Коэффициент экономичности воспроизводства населения равен:
Коэффициент экономичности воспроизводства показывает удельный вес естественного прироста в общем обороте населения. В регионе доля естественного прироста в общем обороте населения составляет 43%. 2. Определим коэффициент жизненности:
3. Абсолютный прирост населения равен: AS - SK - SH = 840 - 820 = 20 тыс. чел., в том числе за счет естественного прироста 16, 6-6, 64=9, 96 тыс. чел., за счет положительного сальдо миграции 20-9, 96=10, 04 тыс. чел. Население региона на 49, 8% 10 04 счет естественного прироста и на 50, 2% 4. Определим коэффициент миграции:
Пример 6. Имеются данные о численности и естественном движении населения региона за 1997-2001 гг.
|

 ,
где
,
где  - величина равного интервала;
- величина равного интервала; 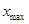 и
и  - максимальные и минимальные значения группировочного признака; n - предполагаемое число групп.
- максимальные и минимальные значения группировочного признака; n - предполагаемое число групп.
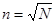 , если число единиц исследуемого объекта меньше 30.
, если число единиц исследуемого объекта меньше 30.
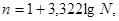 где
где 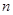 – число групп;
– число групп; 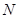 – число единиц совокупности для расчета
– число единиц совокупности для расчета 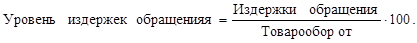
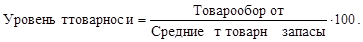
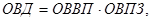 или
или 
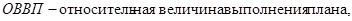
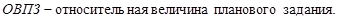
 где
где 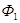 - фактически достигнутый уровень в текущем периоде,
- фактически достигнутый уровень в текущем периоде, 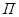 - планируемый показатель на этот же период.
- планируемый показатель на этот же период.
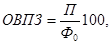 где
где 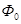 - показатель, достигнутый в предыдущем периоде,
- показатель, достигнутый в предыдущем периоде, 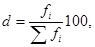
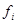 - части единиц совокупности,
- части единиц совокупности,  - сумма всех единиц совокупности.
- сумма всех единиц совокупности.


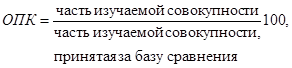
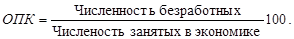
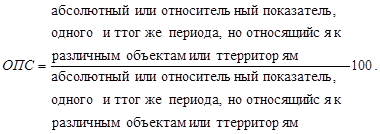
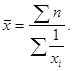
 где
где 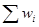 -
- 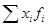
 ,
где
,
где 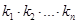 - коэффициенты роста.
- коэффициенты роста.
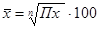 .
.
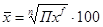
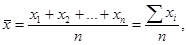 где
где 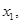
 …
… 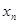 - индивидуальные значения варьирующего признака,
- индивидуальные значения варьирующего признака,  где
где 
 …
… 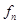 - частота.
- частота.


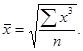
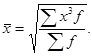
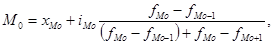 где
где  – нижняя граница модального интервала,
– нижняя граница модального интервала, 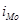 – величина модального интервала,
– величина модального интервала, 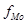 – частота модального интервала,
– частота модального интервала, 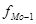 – частота интервала предшествующего модальному интервалу,
– частота интервала предшествующего модальному интервалу, 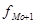 – частота интервала, следующего за модальным интервалом.
– частота интервала, следующего за модальным интервалом.
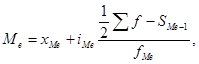 где
где 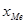 – нижняя граница медианного интервала,
– нижняя граница медианного интервала, 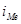 – величина медианного интервала,
– величина медианного интервала, 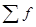 – сумма частот,
– сумма частот, 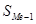 – накопление частот интервала, предшествующего медианному интервалу,
– накопление частот интервала, предшествующего медианному интервалу, 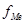 – частота медианного интервала.
– частота медианного интервала.
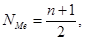 где
где 

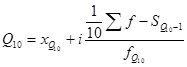 и т.д.
и т.д.
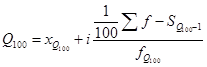 и т.д.
и т.д.
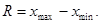
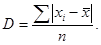


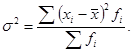

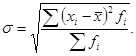

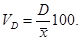
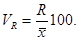
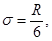


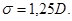

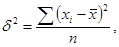

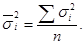
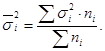

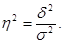
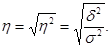
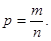
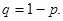
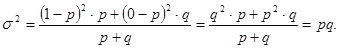
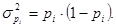
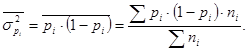
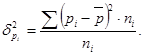
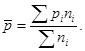

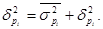
 и
и 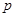

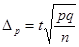
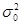 и
и 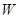

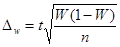
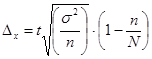
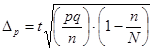

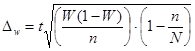
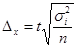


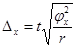


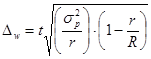
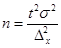

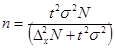



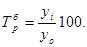
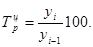
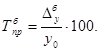
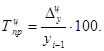
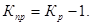
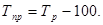
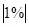
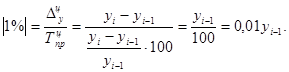


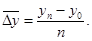

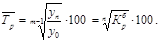
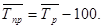
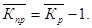
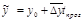


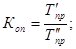
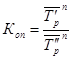
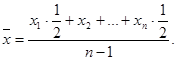
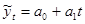
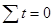
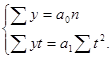

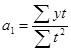
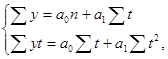
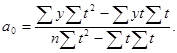
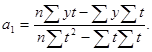

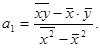

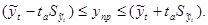

 где
где 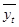 - средний месячный уровень показателя за три и более года,
- средний месячный уровень показателя за три и более года,  — среднемесячное за все годы значение показателя.
— среднемесячное за все годы значение показателя.
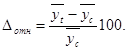
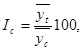 где
где 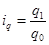
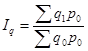
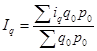

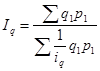
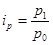
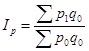
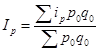

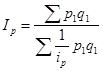
 ,
, 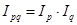
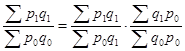
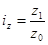

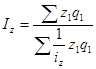
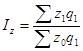 ,
, 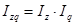

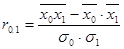 ,
, 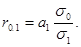
 ,
, 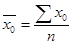 ,
, 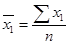 ,
,
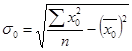 ,
, 




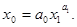

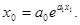
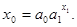
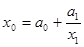
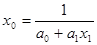
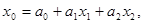
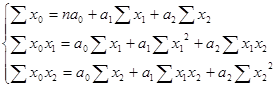

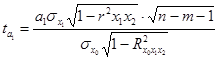
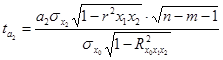
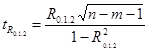


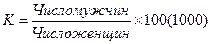 (15)
(15) (16)
(16) :
: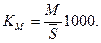 (17)
(17) (18)
(18)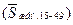 :
: (19)
(19) (20)
(20)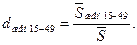
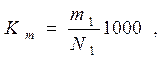 или (21)
или (21)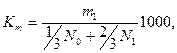 (22)
(22)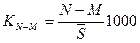 (23)
(23)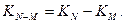 (24)
(24) или
или 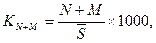 (25)
(25)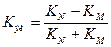 или
или 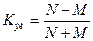 (26)
(26) (27)
(27) (28)
(28)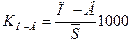 или
или 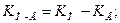 (29)
(29) или
или 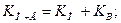 (30)
(30)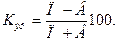 (31)
(31)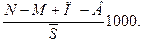 (32)
(32)
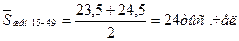
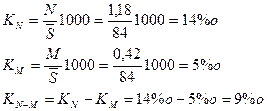
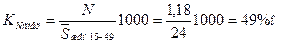
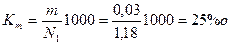
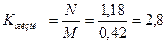 родившихся на одного умершего.
родившихся на одного умершего.
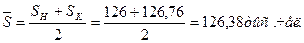
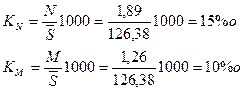

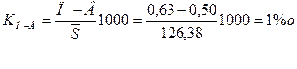

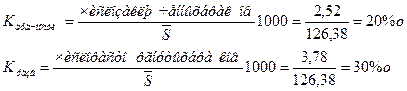
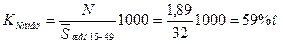
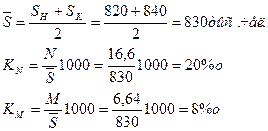

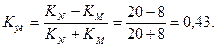
 родившихся на одного умершего.
родившихся на одного умершего. формируется за
формируется за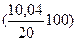 за счет миграции.
за счет миграции.