ИССЛЕДОВАНИЕ ТЕПЛООТДАЧИ ПРИ СВОБОДНОЙ КОНВЕКЦИИ

 

Цель работы: экспериментальное определение коэффициентов теплоотдачи горизонтальной трубы при свободном движении воздуха в неограниченном пространстве, построение уравнения подобия методами теории подобия и математического моделирования.

 

Основные понятия

 

Совместный процесс переноса теплоты конвекцией и теплопроводностью называется конвективным теплообменом.

Причиной конвективного переноса теплоты является неравномерность температурного поля внутри среды. Конвекция возможна только в текучей среде, в которой перенос теплоты неразрывно связан с переносом самой среды.

Различают свободную и вынужденную конвекцию. Свободная конвекция возникает за счет разности плотностей различных частей жидкости в гравитационном поле Земли. Вынужденная возникает при внешнем силовом воздействии на жидкость насосов, компрессоров, вентиляторов, силы ветра и т.д.

Примером свободной конвекции может служить нагревание воздуха в помещении горячей поверхностью отопительного радиатора. Действительно, ближайшие к поверхности слои воздуха нагреваются. Из-за

более высокой температуры плотность воздуха нагретых слоев меньше плотности более удаленных от радиатора слоев воздуха. Появляющаяся разность плотностей приводит к возникновению подъемной силы, которая заставляет более нагретые слои воздуха подниматься вверх. Вместе с переносом теплого воздуха происходит перенос тепловой энергии. Часто встречаемый в инженерной практике случай, когда теплотой обмениваются поток жидкости, с одной стороны, и поверхность твердого тела, с другой, называется конвективной теплоотдачей, или теплоотдачей. Теплоотдача подчиняется закону Ньютона-Рихмана

 

dQ = a · | T_c – Т_ж | · dF,

 

где dQ – элементарный тепловой поток от стенки с поверхностью dF к жидкости, T_c и Т_ж - температуры элемента поверхности стенки и соприкасающейся с ним жидкости, a - коэффициент пропорциональности, получивший название коэффициента теплоотдачи. Если a и температурный напор (T_c – Т_ж) по поверхности не меняются, то закон Ньютона-Рихмана имеет вид

 

Q = a · |T_c – Т_ж| · F, Вт. (4.1)

На теплоотдачу в общем случае оказывают влияние природа возникновения (свободная или вынужденная) и режим движения (ламинарный или турбулентный), теплофизические свойства жидкости (плотность, теплопроводность, теплоемкость, температуропроводность и вязкость), скорость движения жидкости, температуры стенки и жидкости, форма и размеры поверхности и др. факторы.

Основная сложность в использовании уравнения Ньютона-Рихмана заключается в определении коэффициента теплоотдачи. Аналитический путь малоперспективен, т.к. aявляется функцией многих переменных и определяется системами сложных и трудно решаемых дифференциальных уравнений в частных производных.

Поэтому на практике пользуются не табличными значениями, а определяют a из так называемых уравнений подобия. В отличие от обычных уравнений с размерными переменными в них используются безразмерные критерии подобия. Уравнения подобия строятся методами теории подобия и математического моделирования [7].

Наиболее часто для описания процессов конвективного теплообмена и теплоотдачи, в частности, используются следующие критерии подобия:

· Критерий Нуссельта

Nu_ж = a ·ℓ / λ _ж, (4.2)

 

где ℓ - определяющий размер омываемой поверхности, λ _ж – коэффици-

ент теплопроводности жидкости. Физический смысл этого критерия состоит в том, что его величина характеризует интенсивность конвективного теплообмена между жидкостью и поверхностью твердого тела.

· Критерий Грасгофа

Gr_ж = β · g · Δ T · ℓ ³ / v², (4.3)

 

где β – коэффициент объемного расширения жидкости, g – ускорение силы тяжести, Δ T = T_c – T_ж , ν - коэффициент кинематической вязкости жидкости. Критерий Грасгофа характеризует эффективность подъемной силы, обусловливающей свободную конвекцию жидкости.

· Критерий Прандтля

Pr_ж = Pe_ж / Re_ж = (w ·ℓ / a) / (w ·ℓ / ν) = ν / a, (4.4)

где a – коэффициент температуропроводности.

При построении уравнений подобия для свободной конвекции жидкости (газа) в неограниченном пространстве около вертикальных пластин, вертикальных и горизонтальных труб в прямоугольной логарифмической системе координат строятся графики зависимостей

ℓ g (Nu_ж) = f [ℓ g (Gr_ж ∙ Pr_ж)] (4.5)

 

на основе экспериментальных значений коэффициентов теплоотдачи, температур жидкости и стенки, коэффициентов теплопроводности, кинематической вязкости, температуропроводности и др., полученных для конкретных условий.

Поскольку такие графики в логарифмической системе координат с достаточной точностью могут быть аппроксимированы уравнениями прямых, то в обычной прямоугольной системе координат эти уравнения

имеют вид степенных зависимостей

 

Nu_ж = C ∙ (Gr_ж ∙ Pr_ж)^N, (4.6)

 

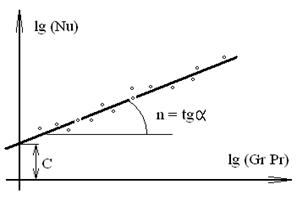
где С и N – числовые коэффициенты, которые получаются в результате обработки экспериментальных значений по методу наименьших квадратов. Графическая интерпретация этих коэффициентов при аппроксимации представлена на рис. 6. Определение коэффициентов С и N является одной из задач лабораторной работы.

При обтекании пластин и труб жидкостью, около их поверхности образуется тепловой пограничный слой (аналогично тому, как это происходит при образовании гидродинамического пограничного слоя).

Уравнения подобия вида (4.6) составляют для расчета локальных и средних коэффициентов теплоотдачи.

Уравнения подобия, предназначенные для расчета локальных коэффициентов, позволяют для поверхности, например, плоской стенки, рассчитывать значения a на заданном расстоянии Х от соответствующего ее края.

Рис. 6. Аппроксимация экспериментальных значений уравнением прямой

 

Из других уравнений подобия могут быть рассчитаны средние для всей поверхности, например, плоской стенки коэффициенты теплоот-дачи.

При расчете теплоотдачи при свободной конвекции в качестве определяющего размера ℓ для горизонтальной пластины используется среднее арифметическое ее длины и ширины, для горизонтальной трубы – ее наружный диаметр. Определяющим размером для вертикальной пластины является ее высота, для вертикальной трубы – ее длина.

Входящие в критерии подобия (4.2) – (4.4) коэффициенты теплопроводности жидкости λ, ее динамической (кинематической) вязкости ν, удельного объема или плотности υ (ρ), коэффициентов объемного расширения β, температуропроводности a берутся по таблицам теплофизических свойств воды и водяного пара [5]. Для других жидкостей и газов рекомендуется использовать справочник [6].

При расчете теплоотдачи при свободной конвекции в качестве определяющей температуры для горизонтальной пластины берется среднее арифметическое температур стенки и жидкости (вдали от поверхности). Для вертикальной пластины, горизонтальной и вертикальной труб определяющей является температура вдали от поверхности.

Для учета изменения свойств теплоносителя по толщине пограничного слоя в уравнение подобия (4.6) может вводиться поправочный коэффициент

ε = (Pr_ж/Pr_с) ^{0, 25}.

 

 

В этом случае уравнение подобия (4.6) принимает вид

 

Nu_ж = C ∙ (Gr_ж ∙ Pr_ж)^N ∙ ε. (4.7)

 

Величина поправочного коэффициента ε существенно отличается от единицы лишь для капельных жидкостей, например, воды. Для газов ε =1, т.к. критерий Pr_ж слабо зависит от температуры.

Значения коэффициентов С, N и ε для расчета теплоотдачи при свободной конвекции из уравнения (4.7) приведены в табл. 3.