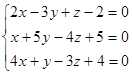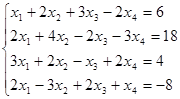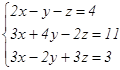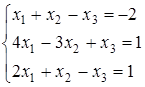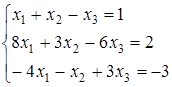Система n лінійних рівнянь з n невідомими
Хай дана лінійна система п рівнянь з п невідомими, де aij bi, (i = 1, 2..., n; j= 1, 2..., n) - довільні числа, звані, відповідно, коефіцієнтами при змінних і вільними членами рівнянь.
Такий запис (1) називається системою лінійних рівнянь в нормальній формі. Рішенням системи (1) називається така сукупність n чисел (х1 = k1, x2=k2, xn=kn), при підстановці яких кожне рівняння системи звертається у вірну рівність. Система рівнянь сумісна, якщо вона має хоч би одне рішення і несумісна, якщо вона не має рішень. Якщо сумісна система рівнянь має єдине рішення, вона називається визначеною; навпаки, система рівнянь називається невизначеною, якщо вона має більш за одне рішення. Дві системи рівнянь є рівносильними або еквівалентними, якщо вони мають одну і ту ж безліч рішень. Система, рівносильна даній може бути отримана за допомогою елементарних перетворень системи (1). Систему можна також записати у вигляді матричного рівняння:
де А — матриця коефіцієнтів при змінних, або матриця системи:
X — матриця-стовпець (вектор) невідомих:
В — матриця-стовпець (вектор) вільних членів:
У розгорненому вигляді систему (1) можна представити таким чином:
Існує ряд методів рішення системи, орієнтованих на обчислення уручну: методи Крамера, Гауса і т.д. Припускаючи використання комп'ютера для проведення обчислень, найдоцільніше розглянути рішення системи в загальному вигляді (метод зворотної матриці). Вважатимемо, що квадратна матриця системи Аnm є невиродженою, тобто її визначник |А| ¹ 0. В цьому випадку існує зворотна матриця А-1. Умножаючи зліва обидві частини матричної рівності на зворотну матрицю А-1 отримаємо: А-1 ´ А ´ Х = А-1´ В, Е ´ Х = А-1 ´ В; Е ´ Х = Х, звідси рішенням системи методом зворотної матриці буде матриця-стовпець
Х = А-1´ В
Таким чином, для вирішення системи (знаходження вектора X) необхідно знайти зворотну матрицю коефіцієнтів і помножити її справа на вектор вільних членів. Виконання цих операцій в пакеті Excel розглянуте у лабораторній роботі «Дії з масивами».
Рішення 1. Введіть матрицю А (в даному випадку розміру 2 х 2) 2. Знайдіть зворотну матрицю А-1. Для цього: § виділите блок осередків під зворотну матрицю. Наприклад, виділіть блок А5: В6; § натисніть на панелі інструментів Стандартна кнопку Вставка функції; § у полі Категорія виберіть Математичні, а в робочому полі Функція — ім'я функції МОБР. Після цього клацніть на кнопці 0К; §
3. Множенням зворотної матриці А-1 на вектор В знайдіть вектор X. Для цього: § § у вікні Майстра функцій в робочому полі Категорія виберіть Математичні, а в робочому полі Функція ім'я функції — МУМН0Ж; § у другому кроці діалогу введіть діапазон зворотної матриці А5: В6 в робоче поле Массив1 (покажчиком миші при натиснутій лівій кнопці), а діапазон матриці В — С2: С3 — в робоче поле Массив2. Після цього натисніть поєднання клавіш CTRL+SHIFT+ENTER; § в результаті в діапазоні С5: С6 з'явиться вектор X. Причому х = 5 буде знаходитися в осередку С5, а у = -4 — в осередку С5. Можна здійснити перевірку знайденого рішення. Для цього знайдений вектор X необхідно підставити в початкове матричне рівняння А× Х= В. Перевірка проводиться таким чином. 1. Виділите блок осередків під результуючу матрицю (під вектор В). Її розмірність буде т × р, в даному прикладі 2× 1. Наприклад, виділите блок осередків D2: D3 (покажчиком миші при натиснутій лівій кнопці). 2. У діалоговому вікні Майстер функцій в робочому полі Категорія виберіть Математичні, а в робочому полі Функція — ім'я функції МУМНОЖ. Клацніть на кнопці ОК. 3. Введіть діапазон початкової матриці А — А2: В3 в робоче поле Массив1 (покажчиком миші при натиснутій лівій кнопці), а діапазон матриці X — С5: С6 - в робоче поле Массив2. Після цього натисніть поєднання клавіш CTRL+SHIFT+ENTER. В результаті в діапазоні D2: D3 з'явиться вектор В, і, якщо система вирішена правильно, вектор, що з'явився, буде рівний результатному В = (7 40).
Вправи Вирішіть самостійно наступні приклади і зробіть перевірку.
|

 (1)
(1) А´ Х = У
А´ Х = У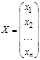


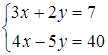 Приклад. Хай необхідно вирішити систему
Приклад. Хай необхідно вирішити систему в діапазон А2: В3; Вектор В = (7 40) введіть в діапазон С2: С3.
в діапазон А2: В3; Вектор В = (7 40) введіть в діапазон С2: С3. у другому кроці діалогу МОБР введіть діапазон початкової матриці А2: В3 в робоче поле Масив (покажчиком миші при натиснутій лівій кнопці). Дії закінчіть натисканням клавіш CTRL+SHIFT+ENTER; В результаті в діапазоні АЗ: В4 з'явиться зворотна матриця:
у другому кроці діалогу МОБР введіть діапазон початкової матриці А2: В3 в робоче поле Масив (покажчиком миші при натиснутій лівій кнопці). Дії закінчіть натисканням клавіш CTRL+SHIFT+ENTER; В результаті в діапазоні АЗ: В4 з'явиться зворотна матриця: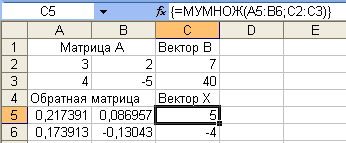 виділіть блок осередків під результуючу матрицю (під вектор X). Її розмірність буде т × р, в даному прикладі 2× 1 Наприклад, виділіть блок осередків С5: С6 (покажчиком миші при натиснутій лівій кнопці);
виділіть блок осередків під результуючу матрицю (під вектор X). Її розмірність буде т × р, в даному прикладі 2× 1 Наприклад, виділіть блок осередків С5: С6 (покажчиком миші при натиснутій лівій кнопці);