Примеры решения задач. Задача 1. ЭДС источника тока =6 В
Задача 1. ЭДС источника тока
Подставив формулу (2) в формулу (1), получим:
Из формулы (3) видно, что при постоянных величинах
Следовательно,
Таким образом, задача сводится к отысканию сопротивления r внутреннего участка цепи (источника тока). Если учесть, что согласно закону Ома (2) для замкнутой цепи наибольшая сила тока I max будет при внешнем сопротивлении R = 0 (ток короткого замыкания), то
Подставив найденное из (5) значение внутреннего сопротивления r в формулу (4), получим:
Мощность тока, выделяемая на внешнем участке цепи, является полезной по отношению к полной мощности источника тока, которая находится по формуле
КПД источника тока равен отношению полезной мощности, выделяемой на внешнем участке цепи, к полной мощности источника тока:
В нашем случае Мощность, теряемую в источнике тока, можно найти по формуле: В нашем случае: Ответ:
Рис.7.1 Указания: Для расчета разветвленных цепей применяются правила Кирхгофа: а) б) На основании этих правил можно составить уравнения, необходимые для определения искомых величин (силы тока, сопротивления и ЭДС). Применяя правила Кирхгофа, следует соблюдать следующие указания: 1. Перед составлением уравнений произвольно выбрать: а) направления токов (если они не заданы по условию задачи) и указать их стрелками на чертеже; б) направления обхода контуров (например, по часовой стрелке). 2. При составлении уравнений по первому правилу Кирхгофа считать токи, подходящие к узлу, положительными, а токи, отходящие от узла, отрицательными. Число уравнений, составляемых по первому правилу Кирхгофа, должно быть на единицу меньше числа узлов, содержащихся в цепи. 3. При составлении уравнений по второму правилу Кирхгофа надо считать, что а) произведение силы тока на сопротивление участка контура IкRк входит в уравнение со знаком “плюс”, если направление тока в данном участке совпадает с выбранным направлением обхода контура, в противном случае произведение IкRк входит в уравнение со знаком “минус”, б) ЭДС входит в уравнение со знаком “плюс”, если она повышает потенциал в направлении обхода контура, т.е. если при обходе приходится идти от минуса к плюсу внутри источника тока; в противном случае ЭДС входит в уравнение со знаком “минус”. Число уравнений, составленных по второму правилу Кирхгофа должно быть равно числу независимых контуров, имеющихся в цепи. Для составления уравнений первый контур можно выбирать произвольно. Все последующие контуры следует выбрать таким образом, чтобы в каждый новый контур входила хотя бы одна ветвь цепи, не участвовавшая ни в одном из ранее использованных контуров. Если при решении уравнений, составленных указанным выше способом, получены отрицательные значения силы тока или сопротивления, то это означает, что ток через данное сопротивление в действительности течет в направлении, противоположном произвольно выбранному. При этом числовые значения силы тока будут правильными. Однако в этом случае неверным окажется вычисленное значение сопротивления. Тогда необходимо, изменив на чертеже направление тока в сопротивлении, составить новую систему уравнений и, решив ее, определить искомое сопротивление.
Выберем направления токов, как они показаны на рисунке, и условимся обходить контуры по часовой стрелке. По первому правилу Кирхгофа для узла F имеем: I 1 – I 2 – I 3 = 0. (1)
 По второму правилу Кирхгофа имеем для контура ACDFA: – I 1 R 1 – I 2 R 2 = – По второму правилу Кирхгофа имеем для контура ACDFA: – I 1 R 1 – I 2 R 2 = –  1, или после умножения обеих частей равенства на – 1: 1, или после умножения обеих частей равенства на – 1:
I 1 R 1 + I 2 R 2 =
Соответственно для контура AFGHA найдем: I 1 R 1 + I 3 R 3 =
После подстановки известных числовых значений в формулы (1), (2) и (3) получим: I 1– I 2–0, 05=0, 50 I 1+25 I 2=1, 100 I +0, 05·20= Перенеся в этих уравнениях неизвестные величины в левые части, а известные – в правые, получим систему 3 уравнений с тремя неизвестными:
Выразим из первого уравнения системы I2 и подставим во второе:
Подставляя I1 в третье уравнение, получаем Ответ:
|

 =5А. Какая наибольшая мощность
=5А. Какая наибольшая мощность  может выделиться на подключенном к источнику тока резисторе с переменным сопротивлением? Каким при этом будет КПД источника тока и какая мощность
может выделиться на подключенном к источнику тока резисторе с переменным сопротивлением? Каким при этом будет КПД источника тока и какая мощность  будет расходоваться на нагревание самого источника?
будет расходоваться на нагревание самого источника? , (1)
, (1)
 =?
=?
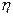 =?
=?

 (2)
где R и r – сопротивления внешнего и внутреннего участков цепи соответственно.
(2)
где R и r – сопротивления внешнего и внутреннего участков цепи соответственно.
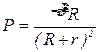 . (3)
. (3) . (4)
. (4) . (5)
. (5) .
. и в нашем случае будет равна
и в нашем случае будет равна . (6)
. (6) . (7)
. (7)
 .
. .
. ;
; 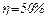 ;
;  .
. Задача 2. Электрическая цепь состоит из двух источников тока, трех сопротивлений и амперметра (рис.7.1). В этой цепи R 1=100 Ом, R 2=50 Ом, R 3=20 Ом, ЭДС одного из источников тока
Задача 2. Электрическая цепь состоит из двух источников тока, трех сопротивлений и амперметра (рис.7.1). В этой цепи R 1=100 Ом, R 2=50 Ом, R 3=20 Ом, ЭДС одного из источников тока  – первое правило Кирхгофа;
– первое правило Кирхгофа; - второе правило.
- второе правило.
 Решение:
Решение:
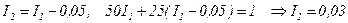 .
. =4 В.
=4 В.


