Тема . Выборочное исследование
Выборочное статистическое исследование – это обследование выборочной совокупности с целью получения достоверных суждений о характеристиках или параметрах генеральной совокупности. Генеральная совокупность – это полная совокупность единиц (статистическая совокупность). Выборочная совокупность (выборка) - это часть единиц генеральной совокупности, отобранная в случайном порядке. Из требования случайности отбора единиц следует, что каждая единица генеральной совокупности имеет равные шансы попасть в выборку. Имеется ряд причин, в силу которых, выборочному наблюдению отдается предпочтение перед сплошным. Наиболее существенны из них следующие: - экономия времени и средств в результате сокращения объема работы (при выборочном методе обследованию подвергается 5-10%, реже до 15-20% изучаемой совокупности); - сведение к минимуму порчи или уничтожения исследуемых объектов (например, при определении прочности пряжи на разрыв нити, при испытании электрических лампочек на продолжительность горения, при проверке консервов на доброкачественность); - исследуемая совокупность может быть полностью недоступна; - исследуемая совокупность может не иметь конечного объема (например, при обследовании опытной партии новых изделий; когда под генеральной совокупностью понимается весь будущий выпуск продукции массовым производством). Наиболее часто исследуемые с помощью выборочного метода характеристики совокупности: 1) Среднее арифметическое значение признака в совокупности: генеральная средняя 2) Доля альтернативного признака: генеральная доля Альтернативный признак – это признак, имеющий 2 значения. Если одно из этих значений принять как заданное, то доля альтернативного признака будет характеризовать долю (удельный вес) единиц в статистической совокупности, которые имеют заданное значение альтернативного признака. Например, доля нестандартных изделий во всей партии товара, удельный вес продукции собственного производства в товарообороте предприятия, удельный вес продавцов в общей численности работников магазина и т.п. 3) дисперсия признака в совокупности: генеральная дисперсия s2= Часто с помощью выборочного метода исследуются не просто характеристики генеральной совокупности, а параметры распределения изучаемого признака генеральной совокупности, если удалось установить (из теоретических соображений), какое именно распределение имеет признак. Например, если известно, что изучаемый признак распределен нормально, то исследуемыми параметрами будут: а - математическое ожидание и s - среднее квадратическое отклонение. Если же есть основания считать, что признак имеет распределение Пуассона, то необходимо оценить параметр l- лямбда, которым это распределение определяется. Введем общее обозначение исследуемой характеристики или параметра – тета q. Характеристику или параметр генеральной совокупности обозначим как qг. По данным выборки мы не можем найти точное значение характеристики или параметра генеральной совокупности, т.е. qг, однако мы можем получить его приближенное значение (оценку). Статистической оценкой (q*) характеристики (параметра) генеральной совокупности называют приближенное значение характеристики (параметра), полученное по некоторой функции от наблюдаемых в выборке значений признака х (х1, х2,...хn), т.е.: q* =f(x1, x2,...xn), где n – объем выборки; (х1, х2,...хn) – рассматриваются как независимые случайные величины. Функцию (f) называют способом оценивания. Значение же, полученное по данной функции от выборочных значений признака х, называют статистической оценкой. В качестве оценок чаще всего используются выборочные показатели (т.е. q*=qв). Например, для q= Очевидно, что от выборки к выборке статистическая оценка (даже при одном и том же способе оценивания) меняется (см. рис.7). Получаемая оценка (q*j) представляет частный случай случайной переменной, т.к. сочетание значений х в выборке случайно, а, следовательно, случайным будет и значение функции от них.
1(n1) 2 (n2)..... m (nm) f1: q*11 q*12 q*1m f2: q*21 q*22 q*2m где nj – объем j-ой выборки; q*ij- оценка qг, полученная по данным j–ой выборки при i–ом способе оценивания; m- число выборок; f1, f2 – соответственно 1-ый и 2-ой способы оценивания qг.
Рис.. Оценивание генеральной характеристики по данным выборки.
Доказано, что для выборок большого объема, которые можно отобрать из одной и той же генеральной совокупности, (а, следовательно, для генеральной совокупности большого объема) предполагается, что сами оценки характеристик распределены по нормальному закону. Для одной и той же характеристики (параметра) генеральной совокупности может быть предложено несколько способов оценивания. Таким образом, возникает проблема выбора лучшего способа оценивания. Критерием выбора является требование состоятельности, несмещенности и эффективности оценки, получаемой при данном способе оценивания. Способ оценивания дает состоятельные оценки, если при бесконечно большом объеме выборки значение статистической оценки стремится к искомому значению характеристики (параметра) генеральной совокупности. Способ оценивания дает несмещенныеоценки, если математическое ожидание оценки при данном способе оценивания тождественно искомой характеристике (параметру) генеральной совокупности (при любом объеме выборки), т.е.М(q*)=qг. Если математическое ожидание оценки не равняется характеристике генеральной совокупности, то оценка называется смещенной. И разность М(q*) - qгназывается смещением. Способ оценивания дает эффективные оценки, если дисперсия оценки минимальна (при заданном объеме выборки n) в сравнении с другими способами оценивания. Ошибки выборки. Статистическая оценка, полученная по данным выборки, отличается от генеральной характеристики (параметра) на величину ошибки наблюдения (регистрации) и ошибки репрезентативности (выборки): q*=qг+ошибка регистрации+ошибка репрезентативности. Будем считать, что ошибка регистрации равна нулю. Понятие репрезентативности было рассмотрено ранее в теме «статистическое наблюдение» (см. лекцию 3). Ошибки репрезентативности делятся на: · систематические – отклонения от схемы (способа отбора); · случайные (ошибки выборки) - это отклонения, возникающие из-за недостаточно равномерного представления в выборочной совокупности различных категорий единиц генеральной совокупности, в силу чего распределение отобранной совокупности единиц не вполне точно воспроизводит распределение единиц генеральной совокупности. Величина случайной ошибки репрезентативности может быть оценена с помощью соответствующих математических методов. Случайная ошибка репрезентативности называется ошибкой выборки. Различают среднюю и предельную ошибки выборки. Средняя ошибкавыборки (m) вычисляется как средняя из возможных ошибок ej, j –номер выборки j=1; m. Она обычно рассчитывается по формуле средней квадратической: В каждой конкретной выборке фактическая ошибка выборки может быть меньше средней ошибки, равна ей или больше ее. Причем каждое из этих расхождений имеет различную вероятность. Предельная ошибка выборки (D) – это максимально возможная при данной вероятности ошибка выборки. То есть мы с заданной вероятностью гарантируем, что ошибка нашей (j-ой) выборки не превысит предельную ошибку D. Вероятность, с которой мы гарантируем, что ошибка нашей выборки не превысит предельную ошибку, называется доверительной вероятностью и обозначается g. Предельная ошибка рассчитывается так: D=t·m, где t- коэффициент доверия, значение которого определяется доверительной вероятностью (g). Чем больше g, тем больше t. Величина случайной ошибки репрезентативности (ошибки выборки) зависит от: 1) способа формирования выборочной совокупности; 2) объема выборки (чем больше объем выборки, тем меньше ошибка); 3) степени колеблемости изучаемого признака в генеральной совокупности (чем больше колеблемость (вариация) признака, тем ошибка больше). Закон больших чисел – методологическая основа выборочного метода. Теоретической основой выборочного метода служит закон больших чисел. Суть данного закона состоит в следующем: с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются (чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик). Математически данный закон записывается через неравенство П.Л.Чебышева:
Следует отметить, что данное неравенство справедливо для генеральной совокупности с ограниченной дисперсией. Неравенство Чебышева доказывает принципиальную возможность определения генеральной средней по данным простой случайной выборки. Центральная предельная теорема А.М.Ляпунова (доказанная в 1901 г.) позволяет указать вероятность появления ошибок определенной величины. Согласно данной теореме при достаточно большом числе независимых наблюдений вероятность того, что расхождение между выборочной и генеральной средней не превзойдет по модулю некоторую величину – t·m, равна интегральной функции распределения вероятностей стандартного нормального распределения Ф(t) (справедливо для генеральной совокупности с конечной средней и ограниченной дисперсией):
Из центральной предельной теоремы следует важный вывод: при достаточно большом числе независимых наблюдений (объеме выборки) распределение отклонений выборочных средних от генеральной средней (а, следовательно, и самих выборочных средних) приближенно нормально. При небольшом объеме выборки (n< 30) Способы отбора. Точечные и интервальные оценки. Отбор может быть организован как повторный или бесповторный. При повторном отборе общая численность единиц генеральной совокупности в процессе выборки остается неизменной. Ту или иную единицу, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами при повторном отборе вновь попасть в выборку. Повторная выборка в социально-экономической жизни встречается редко. При бесповторном отборе единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует; т.е. последующую выборку делают из генеральной совокупности уже без отобранных единиц. Таким образом, при бесповторной выборке численность единиц генеральной совокупности сокращается в процессе выборки. Различают следующие виды отбора: простой собственно-случайный отбор (без предварительного расчленения генеральной совокупности на какие-либо группы) и отбор с предварительным разбиением совокупности на группы. Простой собственно-случайный отбор – такойотбор единиц из генеральной совокупности, когда на включение (исключение) единицы в выборку (из выборки) не может повлиять какой-либо фактор кроме случая. Вероятность включения (исключения) объекта в выборку одинакова. Технически он осуществляется посредством жеребьевки или таблиц случайных чисел. Примером может служить отбор студентами на экзамене экзаменационных билетов. Отбор с предварительным делением исходной совокупности на группы может быть организован разными способами, которым соответствуют свои виды отбора: Механический отбор - это бесповторный отбор элементов из генеральной совокупности, упорядоченной по нейтральному (несущественному для цели исследования) признаку через равные интервалы. В этом случае механический отбор дает хорошие результаты и близок к бесповторному собственно-случайному отбору. Например, отбор каждой 20-й детали с конвейера для проверки ее качества. Здесь нейтральный признак – номер детали. Обычно механический отбор применяют для постепенно формирующейся выборки с заранее неизвестным объемом. Размер интервала в генеральной совокупности равен обратному значению доли выборки. Так, при 2%-ой выборке отбирается и проверяется каждая 50-я единица (1/0, 02), при 5%-ой выборке – каждая 20-ая единица (1/0, 05). Для отбора единиц из неоднородной совокупности применяется так называемый расслоенный (стратифицированный) отбор. Расслоенный отбор используется тогда, когда все единицы генеральной совокупности можно разбить на несколько качественно однородных групп по существенным для цели исследования признакам. Затем из каждой выделенной группы собственно-случайным или механическим способом производится индивидуальный отбор единиц в выборочную совокупность. Если пропорции между группами в выборке совпадают с пропорциями между группами в генеральной совокупности, то имеем типический отбор. Серийный отбор - это случайный отбор из генеральной совокупности не отдельных единиц, а их равновеликих групп (гнезд, серий); при этом внутри отобранных групп обследуют все единицы. Серийный отбор применяют в том случае, когда исследуемый признак колеблется внутри серий незначительно. Применение серийной выборки обусловлено тем, что многие товары для их транспортировки, хранения, продажи упаковываются в пачки, ящики и т.п. Поэтому при контроле качества упакованного товара рациональнее проверить несколько упаковок (серий), чем из всех упаковок отбирать необходимое количество товара. По числу единиц в выборочной совокупности выборки делят на большие (n> 30) и малые (n< 30). Точечные и интервальные оценки. Доверительный интервал. Различают точечное и интервальное оценивание. Точечная оценка - оценка, которой соответствует единственное числовое значение. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. Интервальная оценка - оценка, которой соответствует множество значений из определенного интервала (доверительного интервала). Интервальные оценки позволяют установить точность (величину ошибки выборки) и надежность (вероятность, с которой гарантирован результат оценивания) оценок. Доверительным интервалом называют интервал (q*-D; q*+D), который покрывает неизвестную характеристику (параметр) генеральной совокупности с заданной надежностью (доверительной вероятностью) g, т.е.: P[q*-D< qг< q*+D]=g. Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0, 95; 0, 99 и 0, 999. Вероятность того, что доверительный интервал не покроет генеральную характеристику (параметр) совокупности обозначают a и называют уровнем значимости. a =1-g, т.е. при g=0, 95 a=0, 05; при g=0, 99 a=0, 01. Событие, обладающее столь малой вероятностью, считается практически невозможным. Порядок расчета интервальной оценки (построения доверительного интервала). 1. Определение точечной оценки характеристики (параметра) генеральной совокупности (q*). При оценке генеральной средней наилучшей (в смысле несмещенной состоятельной и эффективной) оценкой будет выборочная средняя. Аналогично при оценке генеральной доли альтернативного признака наилучшей оценкой будет выборочная доля. Однако при оценке генеральной дисперсии наилучшей оценкой будет не выборочная, а исправленная дисперсия: 2. Расчет средней (среднеквадратической) ошибки выборки - m. Формулы расчета средней ошибки выборки -m зависят от способа отбора и от вида оцениваемой характеристики (параметра) генеральной совокупности. Формулы расчета средней ошибки вырки приведены в таблице. Таблица Формулы расчета средней ошибки выборки – μ.
Продолжение табл.
3. Расчет предельной ошибки выборки: При большом объеме выборки значение коэффициента доверия t находим из таблиц интегральной функции стандартного нормального распределения по заданной доверительной вероятности g. Так, для g=0, 95 t=1, 96. При g=0, 99040 t=2, 58. При небольшом объеме выборки (n£ 30) значение t определяют по таблицам интегральной функции распределения Стьюдента. Наряду с абсолютным значением предельной ошибки рассчитывается и относительная предельная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности: 4. Результатом интервального оценивания является доверительный интервал: (q*-D; q*+D). ПРИМЕР. Из партии готовой продукции в порядке механической выборки проверено 50 лампочек на продолжительность горения. Средняя продолжительность горения лампочки оказалась равной 840 ч. при среднем квадратическом отклонении 60 ч. Решение: Для построения доверительного интервала (q*-D; q*+D) в качестве точечной оценки q* возьмем выборочное среднее арифметическое. По условию оно равно 840 ч. Чтобы рассчитать предельную ошибку D=t∙ m нужно определить среднюю ошибку m. В случае механического отбора и оценке среднего воспользуемся формулой:
Значение t найдем по таблицам стандартного нормального распределения. Так как в нашем случае выборка большая, ее объем равный 50 > 30. Если бы выборка была малая (с числом единиц < 30), то нужно было бы пользоваться таблицей распределения Стьюдента. Для Рдов=0, 95 по таблице стандартного нормального распределения t=1, 96. Тогда D=1, 96∙ 8, 6 = 16, 86 (ч.). То есть с вероятностью 0, 95 можно утверждать, что средняя продолжительность горения лампочки в нашей выборке отличается от этой же характеристики в генеральной совокупности на 16, 86 часа. Теперь можем построить доверительный интервал: Вывод: с вероятностью 0, 95 можно утверждать, что средняя продолжительность горения в генеральной совокупности (т.е. во всей партии) будет в пределах от 823 ч. до 857 ч Определение необходимого объема выборки. Другая задача, решаемая с помощью выборочного метода: определение необходимого объема выборки - n при заданной точности (D) и надежности (Рдов) оценивания. Формулы расчета для собственно–случайного отбора: характеристика повторный отбор бесповторный отбор:
среднее
ПРИМЕР. На городской телефонной станции в порядке собственно-случайной выборки проводится обследование телефонных разговоров с целью определения сред.продолжительности разговора. Сколько телефонных разговоров требуется обследовать, чтобы с вероятностью 0, 95 предельная ошибка (точность) при определении средней продолжительности разговора не превышала 1 мин. (В порядке пробного обследования среднее квадратическое отклонение длительности разговора составило 5 мин.) Решение: Необходимый объем выборки можно определить по формуле: Дисперсия (s2) по условию равна 52 = 25. При Рдов=0, 95 t=1, 96. Тогда объем выборки будет равен: Вывод: 96 телефонных разговоров требуется обследовать, чтобы с вероятностью 0, 95 предельная ошибка (точность) при определении средней продолжительности разговора не превышала 1 мин. Контрольные вопросы. 1. Дайте понятие выборочного статистического исследования и опишите условия его проведения. 2. Дайте понятие статистической оценки. Какими свойствами должна обладать «наилучшая» статистическая оценка 3. В чем состоит закон больших чисел. Сформулируйте центральную предельную теорему Ляпунова. 4. Какие виды ошибок выборки рассчитывают в теории выборочного исследования. От чего зависит величина ошибки выборки. 5. Опишите способы отбора единиц: повторный, бесповторный, собственно-случайный, механический, расслоенный, типический, серийный. 6. Что представляют собой точечные и интервальные оценки. Какие точечные оценки будут наилучшими при оценивании среднего арифметического, доли альтернативного признака, дисперсии. 7. Опишите порядок построения доверительного интервала для среднего арифметического и доли альтернативного признака. 8. Опишите порядок определения необходимого объема выборки.
|

 , выборочная средняя
, выборочная средняя  , где N, n – объем генеральной и выборочной совокупности соответственно.
, где N, n – объем генеральной и выборочной совокупности соответственно. , выборочна доля -
, выборочна доля -  .
. , выборочная дисперсия
, выборочная дисперсия  .
. , q*=
, q*=  ; для q=w, q*=
; для q=w, q*= 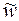 . Однако совсем не обязательно в качестве статистической оценки характеристики (параметра) генеральной совокупности использовать выборочный статистический показатель. Возможны и другие способы оценивания.
. Однако совсем не обязательно в качестве статистической оценки характеристики (параметра) генеральной совокупности использовать выборочный статистический показатель. Возможны и другие способы оценивания. Г.С. (N), qг
Г.С. (N), qг




 В.С.
В.С. .
. 
 .
.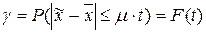 - интегральной функции распределения Стьюдента.
- интегральной функции распределения Стьюдента. .
.




 - остаточная (средняя из внутригрупповых) дисперсия выборки
- остаточная (средняя из внутригрупповых) дисперсия выборки


 -межсерийная дисперсия;
r – число серий в выборке
-межсерийная дисперсия;
r – число серий в выборке

 r- число серий в выборке;
R- число серий в генеральной совокупности
r- число серий в выборке;
R- число серий в генеральной совокупности

 , где t–коэффициент доверия.
, где t–коэффициент доверия. . Относительную предельную ошибку используют как показатель репрезентативности выборки.
. Относительную предельную ошибку используют как показатель репрезентативности выборки.



 доля
доля .
. .
.


